المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | ثابت التكامل Constant og Integration |
 5434
 12:56 صباحاً
التاريخ: 5-11-2015 |
المؤلف : صالح رشيد بطارسه 
الكتاب أو المصدر : معجم الرياضيات 
الجزء والصفحة : 106|
أقرأ أيضاً
التاريخ: 27-4-2018
2259
التاريخ: 10-6-2019
1335
التاريخ: 30-7-2019
1092
التاريخ: 22-9-2019
1215
|
كون التكامل عكس التفاضل , ولأن معنى التفاضل بكل بساطة هو إيجاد المشتقة قَ(س) بمعرفة الاقتران الأصلي ق(س) , فإن عملية التكامل تعني بكل بساطة أيضاً إيجاد الاقتران الأصلي ق(س) بمعرفة مشتقة قَ(س) .
فللأقترانات :
ق1(س) = س2
ق2(س) = س2 + 5
ق3(س) = س2 – 7
1
ق4(س) = س2 + ـــــــــــــــ
2
.
.
.
وهكذا .
جميعاً مشتقة واحدة هي قَ(س) = 2س
والآن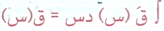 
الاقتران الأصلي
والاقتران الأصلي هو أي اقتران من الاقترانات السابقة , لذلك اصطلح أن يكون الاقتران الأصلي هو ق(س) = س2 + جـ
كون قَ(س) = 2س فقط
ليكون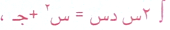 
عندها يسمى العدد جــ ثابت التكامل وهو عدد حقيقي , ج∊ح ومشتقته الاولى=صفر.
|
|
|
|
لصحة القلب والأمعاء.. 8 أطعمة لا غنى عنها
|
|
|
|
|
|
|
حل سحري لخلايا البيروفسكايت الشمسية.. يرفع كفاءتها إلى 26%
|
|
|
|
|
|
|
قسم الشؤون الفكرية يقيم الحفل الختامي لمسابقة حفظ قصار السور للناشئة في أفريقيا
|
|
|
