


 الفيزياء الكلاسيكية
الفيزياء الكلاسيكية
 الكهربائية والمغناطيسية
الكهربائية والمغناطيسية
 علم البصريات
علم البصريات
 الفيزياء الحديثة
الفيزياء الحديثة
 النظرية النسبية
النظرية النسبية
 الفيزياء النووية
الفيزياء النووية
 فيزياء الحالة الصلبة
فيزياء الحالة الصلبة
 الليزر
الليزر
 علم الفلك
علم الفلك
 المجموعة الشمسية
المجموعة الشمسية
 الطاقة البديلة
الطاقة البديلة
 الفيزياء والعلوم الأخرى
الفيزياء والعلوم الأخرى
 مواضيع عامة في الفيزياء
مواضيع عامة في الفيزياء|
أقرأ أيضاً
التاريخ: 23-7-2016
التاريخ: 27-6-2016
التاريخ: 3-7-2016
التاريخ: 19-9-2020
|
So far, we have not dealt with temperature; we have purposely been avoiding the temperature. As we compress a gas, we know that the energy of the molecules increases, and we are used to saying that the gas gets hotter; we would like to understand what this has to do with the temperature. If we try to do the experiment, not adiabatically but at what we call constant temperature, what are we doing? We know that if we take two boxes of gas and let them sit next to each other long enough, even if at the start they were at what we call different temperatures, they will in the end come to the same temperature. Now what does that mean? That means that they get to a condition that they would get to if we left them alone long enough! What we mean by equal temperature is just that—the final condition when things have been sitting around interacting with each other long enough.
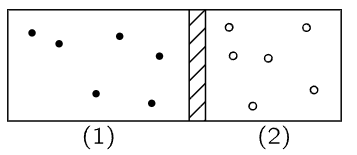
Fig. 39–2. Atoms of two different monatomic gases are separated by a movable piston.
Let us consider, now, what happens if we have two gases in containers separated by a movable piston as in Fig. 39–2 (just for simplicity we shall take two monatomic gases, say helium and neon). In container (1) the atoms have mass m1, velocity v1, and there are n1 per unit volume, and in the other container the atoms have mass m2, velocity v2, there are n2 atoms per unit volume. What are the conditions for equilibrium?
Obviously, the bombardment from the left side must be such that it moves the piston to the right and compresses the other gas until its pressure builds up, and the thing will thus slosh back and forth, and will gradually come to rest at a place where the pressures are equal on both sides. So, we can arrange that the pressures are equal; that just means that the internal energies per unit volume are equal, or that the numbers n times the average kinetic energies on each side are equal. What we have to try to prove, eventually, is that the numbers themselves are equal. So far, all we know is that the numbers times the kinetic energies are equal,
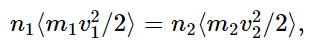
from (39.8), because the pressures are equal. We must realize that this is not the only condition over the long run, but something else must happen more slowly as the true complete equilibrium corresponding to equal temperatures sets in.
To see the idea, suppose that the pressure on the left side were developed by having a very high density but a low velocity. By having a large n and a small v, we can get the same pressure as by having a small n and a large v. The atoms may be moving slowly but be packed nearly solidly, or there may be fewer but they are hitting harder. Will it stay like that forever? At first, we might think so, but then we think again and find we have forgotten one important point. That is, that the intermediate piston does not receive a steady pressure; it wiggles, just like the eardrum that we were first talking about, because the bangings are not absolutely uniform. There is not a perpetual, steady pressure, but a tattoo—the pressure varies, and so the thing jiggles. Suppose that the atoms on the right side are not jiggling much, but those on the left are few and far between and very energetic. The piston will, now and then, get a big impulse from the left, and will be driven against the slow atoms on the right, giving them more speed. (As each atom collides with the piston, it either gains or loses energy, depending upon whether the piston is moving one way or the other when the atom strikes it.) So, as a result of the collisions, the piston finds itself jiggling, jiggling, jiggling, and this shakes the other gas—it gives energy to the other atoms, and they build up faster motions, until they balance the jiggling that the piston is giving to them. The system comes to some equilibrium where the piston is moving at such a mean square speed that it picks up energy from the atoms at about the same rate as it puts energy back into them. So the piston picks up a certain mean irregularity in speed, and it is our problem to find it. When we do find it, we can solve our problem better, because the gases will adjust their velocities until the rate at which they are trying to pour energy into each other through the piston will become equal.
It is quite difficult to figure out the details of the piston in this particular circumstance; although it is ideally simple to understand, it turns out to be a little harder to analyze. Before we analyze that, let us analyze another problem in which we have a box of gas but now we have two different kinds of molecules in it, having masses m1 and m2, velocities v1 and v2, and so forth; there is now a much more intimate relationship. If all of the No. 2 molecules are standing still, that condition is not going to last, because they get kicked by the No. 1 molecules and so pick up speed. If they are all going much faster than the No. 1 molecules, then maybe that will not last either—they will pass the energy back to the No. 1 molecules. So, when both gases are in the same box, the problem is to find the rule that determines the relative speeds of the two.
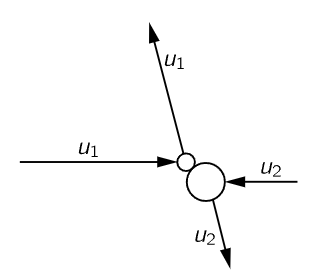
Fig. 39–3. A collision between unequal atoms, viewed in the CM system. u1=|v1−vCM|, u2=|v2−vCM|.
This is still a very difficult problem, but we will solve it as follows. First, we consider the following sub-problem (again this is one of those cases where—never mind the derivation—in the end the result is very simple to remember, but the derivation is just ingenious). Let us suppose that we have two molecules, of different mass, colliding, and that the collision is viewed in the center-of-mass (CM) system. In order to remove a complication, we look at the collision in the CM. As we know from the laws of collision, by the conservation of momentum and energy, after the molecules collide the only way, they can move is such that each maintains its own original speed—and they just change their direction. So, we have an average collision that looks like that in Fig. 39–3. Suppose, for a moment, that we watch all the collisions with the CM at rest. Suppose we imagine that they are all initially moving horizontally. Of course, after the first collision some of them are moving at an angle. In other words, if they were all going horizontally, then at least some would later be moving vertically. Now in some other collision, they would be coming in from another direction, and then they would be twisted at still another angle. So even if they were completely organized in the beginning, they would get sprayed around at all angles, and then the sprayed ones would get sprayed some more, and sprayed some more, and sprayed some more. Ultimately, what will be the distribution? Answer: It will be equally likely to find any pair moving in any direction in space. After that further collisions could not change the distribution.
They are equally likely to go in all directions, but how do we say that? There is of course no likelihood that they will go in any specific direction, because a specific direction is too exact, so we have to talk about per unit “something.” The idea is that any area on a sphere centered at a collision point will have just as many molecules going through it as go through any other equal area on the sphere. So the result of the collisions will be to distribute the directions so that equal areas on a sphere will have equal probabilities.
Incidentally, if we just want to discuss the original direction and some other direction an angle θ from it, it is an interesting property that the differential area of a sphere of unit radius is sinθ dθ times 2π (see Fig. 32–1). And sinθ dθ is the same as the differential of −cosθ. So, what it means is that the cosine of the angle θ between any two directions is equally likely to be anything from −1 to +1.
Next, we have to worry about the actual case, where we do not have the collision in the CM system, but we have two atoms which are coming together with vector velocities v1 and v2. What happens now? We can analyze this collision with the vector velocities v1 and v2 in the following way: We first say that there is a certain CM; the velocity of the CM is given by the “average” velocity, with weights proportional to the masses, so the velocity of the CM is vCM=(m1v1+m2v2)/(m1+m2). If we watch this collision in the CM system, then we see a collision just like that in Fig. 39–3, with a certain relative velocity w coming in. The relative velocity is just v1−v2. Now the idea is that, first, the whole CM is moving, and in the CM there is a relative velocity w, and the molecules collide and come off in some new direction. All this happens while the CM keeps right on moving, without any change.
Now then, what is the distribution resulting from this? From our previous argument we conclude this: that at equilibrium, all directions for w are equally likely, relative to the direction of the motion of the CM.1 There will be no particular correlation, in the end, between the direction of the motion of the relative velocity and that of the motion of the CM. Of course, if there were, the collisions would spray it about, so it is all sprayed around. So the cosine of the angle between w and vCM is zero on the average. That is,
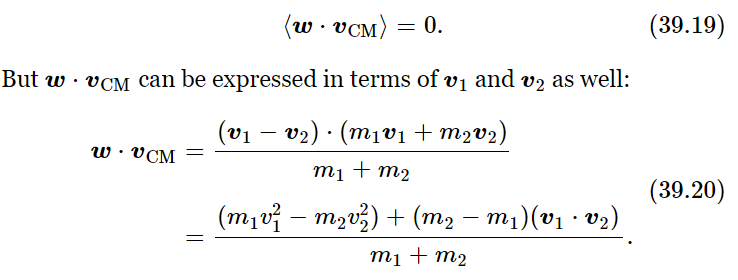
First, let us look at the v1⋅v2; what is the average of v1⋅v2? That is, what is the average of the component of velocity of one molecule in the direction of another? Surely there is just as much likelihood of finding any given molecule moving one way as another. The average of the velocity v2 in any direction is zero. Certainly, then, in the direction of v1, v2 has zero average. So, the average of v1⋅v2 is zero! Therefore, we conclude that the average of m1v21 must be equal to the average of m2v22. That is, the average kinetic energy of the two must be equal:
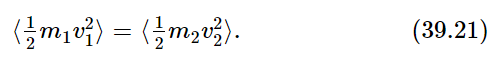
If we have two kinds of atoms in a gas, it can be shown, and we presume to have shown it, that the average of the kinetic energy of one is the same as the average of the kinetic energy of the other, when they are both in the same gas in the same box in equilibrium. That means that the heavy ones will move slower than the light ones; this is easily shown by experimentation with “atoms” of different masses in an air trough.
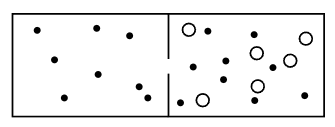
Fig. 39–4. Two gases in a box with a semipermeable membrane.
Now we would like to go one step further, and say that if we have two different gases separated in a box, they will also have equal average kinetic energy when they have finally come to equilibrium, even though they are not in the same box. We can make the argument in a number of ways. One way is to argue that if we have a fixed partition with a tiny hole in it (Fig. 39–4) so that one gas could leak out through the holes while the other could not, because the molecules are too big, and these had attained equilibrium, then we know that in one part, where they are mixed, they have the same average kinetic energy, but some come through the hole without loss of kinetic energy, so the average kinetic energy in the pure gas and in the mixture must be the same. That is not too satisfactory, because maybe there are no holes, for this kind of molecule, that separate one kind from the other.
Let us now go back to the piston problem. We can give an argument which shows that the kinetic energy of this piston must also be 1/2 m2v22. Actually, that would be the kinetic energy due to the purely horizontal motion of the piston, so, forgetting its up and down motion, it will have to be the same as 1/2 m2v22x. Likewise, from the equilibrium on the other side, we can prove that the kinetic energy of the piston is 1/2 m1v21x. Although this is not in the middle of the gas, but is on one side of the gas, we can still make the argument, although it is a little more difficult, that the average kinetic energy of the piston and of the gas molecules are equal as a result of all the collisions.
If this still does not satisfy us, we may make an artificial example by which the equilibrium is generated by an object which can be hit on all sides. Suppose that we have a short rod with a ball on each end sticking through the piston, on a frictionless sliding universal joint. Each ball is round, like one of the molecules, and can be hit on all sides. This whole object has a certain total mass, m. Now, we have the gas molecules with mass m1 and mass m2 as before. The result of the collisions, by the analysis that was made before, is that the kinetic energy of m because of collisions with the molecules on one side must be 1/2 m1v21, on the average. Likewise, because of the collisions with molecules on the other side, it has to be 1/2 m2v22 on the average. So, therefore, both sides have to have the same kinetic energy when they are in thermal equilibrium. So, although we only proved it for a mixture of gases, it is easily extended to the case where there are two different, separate gases at the same temperature.
Thus when we have two gases at the same temperature, the mean kinetic energy of the CM motions are equal.
The mean molecular kinetic energy is a property only of the “temperature.” Being a property of the “temperature,” and not of the gas, we can use it as a definition of the temperature. The mean kinetic energy of a molecule is thus some function of the temperature. But who is to tell us what scale to use for the temperature? We may arbitrarily define the scale of temperature so that the mean energy is linearly proportional to the temperature. The best way to do it would be to call the mean energy itself “the temperature.” That would be the simplest possible function. Unfortunately, the scale of temperature has been chosen differently, so instead of calling it temperature directly we use a constant conversion factor between the energy of a molecule and a degree of absolute temperature called a degree Kelvin. The constant of proportionality is k=1.38×10−23 joule for every degree Kelvin. 2 So if T is absolute temperature, our definition says that the mean molecular kinetic energy is 3/2 kT. (The 3/2 is put in as a matter of convenience, so as to get rid of it somewhere else.)
We point out that the kinetic energy associated with the component of motion in any particular direction is only 1/2 kT. The three independent directions that are involved make it 3/2 kT.
________________________________________________________
Margins
1- This argument, which was the one used by Maxwell, involves some subtleties. Although the conclusion is correct, the result does not follow purely from the considerations of symmetry that we used before, since, by going to a reference frame moving through the gas, we may find a distorted velocity distribution. We have not found a simple proof of this result.
2- The centigrade scale is just this Kelvin scale with a zero chosen at 273.15∘K, so T=273.15+centigrade temperature.



|
|
|
|
لصحة القلب والأمعاء.. 8 أطعمة لا غنى عنها
|
|
|
|
|
|
|
حل سحري لخلايا البيروفسكايت الشمسية.. يرفع كفاءتها إلى 26%
|
|
|
|
|
|
|
جامعة الكفيل تحتفي بذكرى ولادة الإمام محمد الجواد (عليه السلام)
|
|
|