


 الفيزياء الكلاسيكية
الفيزياء الكلاسيكية
 الكهربائية والمغناطيسية
الكهربائية والمغناطيسية
 علم البصريات
علم البصريات
 الفيزياء الحديثة
الفيزياء الحديثة
 النظرية النسبية
النظرية النسبية
 الفيزياء النووية
الفيزياء النووية
 فيزياء الحالة الصلبة
فيزياء الحالة الصلبة
 الليزر
الليزر
 علم الفلك
علم الفلك
 المجموعة الشمسية
المجموعة الشمسية
 الطاقة البديلة
الطاقة البديلة
 الفيزياء والعلوم الأخرى
الفيزياء والعلوم الأخرى
 مواضيع عامة في الفيزياء
مواضيع عامة في الفيزياء|
أقرأ أيضاً
التاريخ: 2024-02-04
التاريخ: 2024-09-12
التاريخ: 2024-02-11
التاريخ: 28-12-2016
|
مثال 2–1 (اتزان استاتيكي لكتلة على الأرض). في أول مثال للاتزان، دعنا نعتبر كتلة ساكنة على الأرضية. نفترض هنا أن الكتلة يمكن التعامل معها على أنها «كتلة نقطية» تتبع قانون نيوتن الأول. حتى لو لم تكُن الكتلة صغيرة جدًّا، فإننا سنرى حالا أن قانون نيوتن الثالث يبرر اعتبارها «كتلة نقطية».
تؤثر قوتان على الكتلة: تشد الكرة الأرضية الكتلة لأسفل وتدفع أرضية الغرفة الكتلة لأعلى. ولأنه ينبغي للقوة الكلية على الكتلة أن تتلاشى، فلا بد أن تكون القوتان متساويتين في المقدار ومتضادتين في الاتجاه. رغم أنهما مختلفتان تمامًا من حيث المنشأ. فالشد الذي تؤثر به الكرة الأرضية لأسفل (يسمى عادة «الجاذبية» أو «الوزن» في الاصطلاح الشائع) هو ببساطة المجموع المتجهي لقوى الجاذبية التي تؤثر على الكتلة بواسطة كل جزيء من جزيئات الكرة الأرضية. إن النسبة التي تسهم بها الجزيئات القريبة (في نطاق بضعة أميال من الكتلة) في هذا المجموع تكون مهملة، وقوة الجذب المؤثرة على الكتلة ناجمة في الأساس عن انجذاب الكتلة إلى الجزيئات البعيدة؛ لأن عدد الجزيئات البعيدة كبير للغاية من الناحية الأخرى، القوة التي تؤثر بها أرضية الغرفة لأعلى هي قوة كهربية قصيرة المدى جدًّا (وهي قوة «التماس» التي ذكرناها بالفعل) تؤثر بها الجزيئات الموجودة بسطح أرضية الغرفة على الجزيئات الموجودة في أسفل الكتلة.
يسمى مقدار قوة الجاذبية التي تؤثر بها الكرة الأرضية على جسم ما وزن الجسم، وعادة ما يرمز له بالحرف W تعتمد قيمة W العددية على ما نختاره ليكون وحدة القوة. فيما يسمى بالنظام البريطاني للوحدات، لا يكون الفأر هو وحدة القوة وإنما الرطل. يمكن تعريف الرطل بأنه قوة الجاذبية التي تؤثر بها الكرة الأرضية على جسم معياري معين موضوع في مكان محدد على سطح الكرة الأرضية. فمثلا: يمكن أن يكون هذا الجسم 454 سنتيمترًا مكعبًا (27.70 بوصة مكعبة) من الماء عند درجة حرارة 4 درجات مئوية وتحت الضغط الجوي، وموجودًا في تقاطع شارع الثالث والثلاثين مع شارع والانت بمدينة فيلادلفيا. أما . وحدة القوة في النظام المتري فهي النيوتن، وتساوي تقريبا 0.2525 رطلا. [لاحظ أن محرك البحث جوجل سوف يقوم بإجراء العديد من التحويلات الشائعة بالنيابة عنك ليست هناك حاجة لحفظ معاملات تحويل معينة. غير أنه من المفيد معرفة (على أقل تقدير) معاملات التحويل الشائعة، مثلا: متر ↔ قدم، سنتيمتر ↔ بوصة، كيلووات ↔ حصان، وغيرها.] غالبًا ما نختصر وحدة النيوتن إلى الحرف N ومن المفيد دائمًا إنشاء مخطط جسم حر تُمَثَّل فيه كل من القوى المؤثرة على الجسم بواسطة متجه. عادة ما تُرسم جميع المتجهات نابعة من مصدر مشترك. إذا كان الجسم في حالة اتزان فإن المجموع المتجهي لجميع القوى في مخطط الجسم الحر يكون صفرًا. مخطط الجسم الحر في المثال الحالي بسيط للغاية (شكل 2–2) ولا يضيف شيئًا لوصفنا الحرفي. في الأمثلة الأكثر أهمية التالية، يمكن الحصول على استنتاجات مقاديرية من الرسم البياني للجسم الحر.
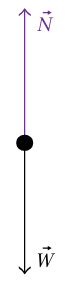
شكل 2–2: مخطط الجسم الحر لكتلة مستقرة على أرضية الغرفة.  هي قوة الجاذبية التي تؤثر بها الكرة الأرضية على الكتلة.
هي قوة الجاذبية التي تؤثر بها الكرة الأرضية على الكتلة. 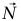 هي قوة التماس التي تؤثر بها أرضية الغرفة على الكتلة.
هي قوة التماس التي تؤثر بها أرضية الغرفة على الكتلة.
مثال 2–2 (كتلة في حالة اتزان على منحدر لا احتكاكي). اعتبر كتلة في حالة اتزان على مستوى مائل أملس. تشد الكرة الأرضية الكتلة لأسفل ويؤثر المستوى على الكتلة بقوة تماس في اتجاه متعامد على المستوى من المؤكد أن هناك ضرورة لأن تؤثر قوة ثالثة على الكتلة لكي تجعلها في حالة اتزان نعلم من الخبرة أن اتجاه هذه القوة الثالثة لا يتحدد بطريقة وحيدة. فمثلا، يمكن الحفاظ على اتزان الكتلة بقوة مناسبة تؤثر موازية للمستوى في الاتجاه الصاعد (شكل 2–3) أو بقوة أفقية مناسبة (شكل 2–4). في الواقع، هناك متَّصَل من الاتجاهات المحتملة للقوة الثالثة. ولكي تكون الكتلة في وضع اتزان، لابد ان يكون للقوة الثالثة المقدار المناسب. وهو ما يعتمد على الاتجاه الذي تؤثر فيه.
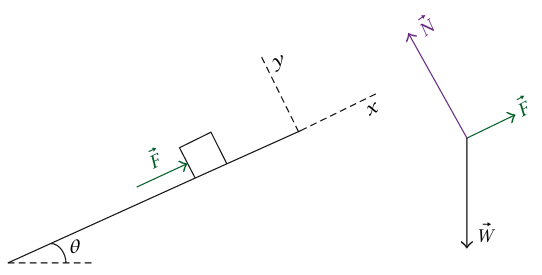
شكل 2–3: الكتلة مُثَبَّتة في مكانها بواسطة قوة تؤثر في اتجاه مواز للمنحدر. يتضمن مخطط الجسم الحر ثلاث قوى.
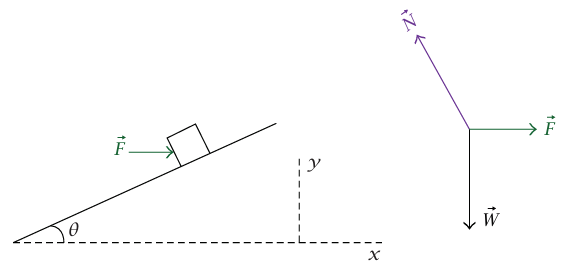
شكل 2–4: هذه المرة ثُبتت الكتلة في مكانها بواسطة قوة مؤثّرة أفقيًّا.
(أ) دعنا ننظر أولًا للحالة التي تُطَبَّق فيها القوة الثالثة في اتجاه مواز للمنحدر. يعرض مخطط الجسم الحر القوى المؤثرة على الكتلة.  هي قوة الجاذبية المؤثرة بواسطة الكرة الأرضية،
هي قوة الجاذبية المؤثرة بواسطة الكرة الأرضية،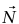 هي قوة التماس المؤثرة بواسطة المنحدر و
هي قوة التماس المؤثرة بواسطة المنحدر و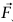 هي القوة الثالثة. أظهرنا هذه القوة لتبين دفعة من أسفل موازية للمنحدر، لكن ينتج نفس مخطط الجسم الحر من «شد» في اتجاه مواز للمنحدر من نقطة تماس على جانب الجسم ناحية الاتجاه الصاعد. يمكن في الحالة الثانية توفير هذه القوة بواسطة وتر؛ حيث تكون
هي القوة الثالثة. أظهرنا هذه القوة لتبين دفعة من أسفل موازية للمنحدر، لكن ينتج نفس مخطط الجسم الحر من «شد» في اتجاه مواز للمنحدر من نقطة تماس على جانب الجسم ناحية الاتجاه الصاعد. يمكن في الحالة الثانية توفير هذه القوة بواسطة وتر؛ حيث تكون  عندئذ هي الشد في الوتر. نرغب في حساب
عندئذ هي الشد في الوتر. نرغب في حساب 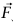 و
و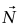 .
.
ينص قانون نيوتن الأول على:

هذه معادلة متجهيَّة، وتكون صحيحة فقط إذا كان مجموع مركبات x للمتجهات الثلاثة صفرًا وكان مجموع مركبات y صفرًا أيضًا. يمكننا اختيار اتجاهي المحورين x وy بالكيفية التي تلائمنا، والاختيار الأكثر ملاءمة هو أن يكون المحور x موازيًا للمنحدر والمحور y عموديا على المنحدر. عندئذٍ تكون مركبتا x وy للمعادلة (1–2) هما:

وبذلك يكون θ F = W sin وθ N = W cos. لاحظ أننا لو أخذنا المحور x في الاتجاه الأفقي والمحور y في الاتجاه الرأسي، لكانت مركبتا x وy للمعادلة (1–2) هما 0 = θ F cos θ – N sin، و 0 = sin θ + N cos θ – W F، وهو ما يؤدي مرة أخرى إلى N = W cos θ, F = W sin θ.
(ب) إذا أثرت القوة الثالثة في الاتجاه الأفقي (نسميها 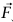 مرة أخرى)، فإن مخطط الجسم الحر يكون كما بالشكل (4–2) . إذا أخذنا المحور x في الاتجاه الأفقي والمحور y في الاتجاه الرأسي، تكون مركبات المعادلة المتجهية
مرة أخرى)، فإن مخطط الجسم الحر يكون كما بالشكل (4–2) . إذا أخذنا المحور x في الاتجاه الأفقي والمحور y في الاتجاه الرأسي، تكون مركبات المعادلة المتجهية 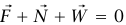 هي 0 = θ F – N sin و0 = N cos θ – W؛ وبذلك يكون θ N = W / cos وθF = W tan. لاحظ التعبيرين المختلفين لحساب N في هذه الحالة والحالة السابقة، ولاحظ أيضًا أن F في هذه الحالة تصبح لا نهائية كلما اقتربت θ من 90o. هل يتفق هذا مع «حدسك الفيزيائي»؟
هي 0 = θ F – N sin و0 = N cos θ – W؛ وبذلك يكون θ N = W / cos وθF = W tan. لاحظ التعبيرين المختلفين لحساب N في هذه الحالة والحالة السابقة، ولاحظ أيضًا أن F في هذه الحالة تصبح لا نهائية كلما اقتربت θ من 90o. هل يتفق هذا مع «حدسك الفيزيائي»؟
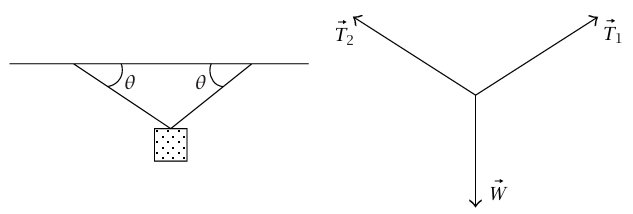
شكل 2–5: رسم توضيحي ومخطط الجسم الحر للمثال 2–3.
مثال 2–3 (كتلة معلقة من السقف بوترين). اعتبر كتلة معلقة بوترين متساويي الطول، كلٌّ منهما متصل بالسقف ويصنع زاوية θ مع الاتجاه الأفقي (انظر شكل 2–5) يعرض مخطط الجسم الحر القوى المؤثرة على الكتلة. 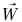 هي قوة الجاذبية المؤثرة بواسطة الكرة الأرضية و
هي قوة الجاذبية المؤثرة بواسطة الكرة الأرضية و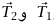 هما القوتان المؤثرتان بواسطة الوترين. من التماثل الموجود في المسألة يتأكد لنا أن
هما القوتان المؤثرتان بواسطة الوترين. من التماثل الموجود في المسألة يتأكد لنا أن 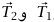 لهما نفس المقدار، الذي سنسميه T. إذا أخذنا المحور x في الاتجاه الأفقي والمحور y في الاتجاه الرأسي، تكون مركبتا المعادلة المتجهية
لهما نفس المقدار، الذي سنسميه T. إذا أخذنا المحور x في الاتجاه الأفقي والمحور y في الاتجاه الرأسي، تكون مركبتا المعادلة المتجهية 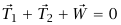 هما:
هما:
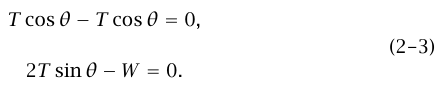
لا تخبرنا المعادلة الأولى من هاتين المعادلتين شيئًا إلا أنها تؤكد وحسب افتراضنا بأن الشد في كلٌّ من الوترين يكون متساويًا. وتخبرنا الثانية بأن الشد المطلوب في الوترين هو (θ T = W/ (2 sin.
لاحظ أن الشد T يصبح كبيرًا جدًّا عندما تكون θ صغيرة جدًّا (في الواقع ∞→T عندما 0→θ). وهكذا نرى أن أي قوة جانبية متواضعة تُطَبَّق على سلك مشدود يمكنها كسر هذا السلك. ومع ذلك، إذا أثرنا بقوة جانبية في منتصف حبل مربوط من مادة النايلون، فإن الحبل سيتمدد، ولأن θ لا تظل صغيرة، فإن الشد في الحبل لن يصبح كبيرًا جدًّا.
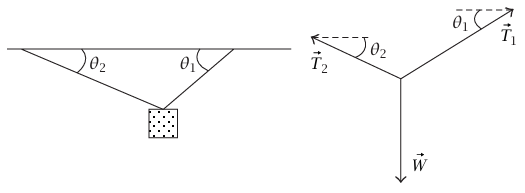
شكل 2–6: رسم توضيحي ومخطط الجسم الحر للمثال 2–4.
مثال 2–4 (كتلة معلقة من السقف بواسطة وترين مختلفين في الطول). قد يكون الوتران في المثال السابق مختلفي الطول بحيث 2θ≠ 1 θشكل 2–6). لاحظ أنه يجب ربط كل من الوترين بالكتلة على حدة. ( لو كانت الكتلة معلقة من حلقة تنزلق بحرية على الوتر، فإن الكتلة ستنزلق حتى يصبح 2θ= 1θ. في المثال الحالي 1T≠T2 وتكون مركبتا معادلة القوة هما:

لاحظ أنه عندما تكون 2θ= 1θ فإن النتيجة تتفق مع نتيجة المثال السابق.



|
|
|
|
لصحة القلب والأمعاء.. 8 أطعمة لا غنى عنها
|
|
|
|
|
|
|
حل سحري لخلايا البيروفسكايت الشمسية.. يرفع كفاءتها إلى 26%
|
|
|
|
|
|
|
جامعة الكفيل تحتفي بذكرى ولادة الإمام محمد الجواد (عليه السلام)
|
|
|