


 الفيزياء الكلاسيكية
الفيزياء الكلاسيكية
 الكهربائية والمغناطيسية
الكهربائية والمغناطيسية
 علم البصريات
علم البصريات
 الفيزياء الحديثة
الفيزياء الحديثة
 النظرية النسبية
النظرية النسبية
 الفيزياء النووية
الفيزياء النووية
 فيزياء الحالة الصلبة
فيزياء الحالة الصلبة
 الليزر
الليزر
 علم الفلك
علم الفلك
 المجموعة الشمسية
المجموعة الشمسية
 الطاقة البديلة
الطاقة البديلة
 الفيزياء والعلوم الأخرى
الفيزياء والعلوم الأخرى
 مواضيع عامة في الفيزياء
مواضيع عامة في الفيزياء|
أقرأ أيضاً
التاريخ: 29-12-2016
التاريخ: 8-2-2016
التاريخ: 27-1-2016
التاريخ: 18-5-2016
|
كان نيوتن معنيًّا في المقام الأول بتفسير حركات الكواكب الملاحظة في المجموعة الشمسية وحركة أقمارها، وأتيح له قدر كبير من بيانات الملاحظات، وكانت الحقائق الأكثر أهمية في نظره هي ما يلي:
(أ) أقمار المشتري تتحرك في مدارات دائرية أساسًا حول المشتري بأزمان دورية تتناسب مع أبعادها عند مركز المشتري مرفوعة للأس 2/3. (يُعرف الزمن الدوري بأنه الزمن اللازم لكي يتم القمر دورة كاملة حول المشتري. إذا أخذنا 0 = t عند اللحظة التي يكون فيها المتجه من مركز المشتري إلى القمر مشيرًا إلى اتجاه خاص بالنسبة إلى خلفية النجوم الثابتة، فإن الزمن الدوري T يكون الزمن المنقضي إلى أن يشير هذا المتجه مرة ثانية إلى نفس الاتجاه. لاحظ الدور المهم للنجوم الثابتة في إمدادنا بتعريف فيزيائي لفئة من المحاور غير الدوارة.)
(ب) الأمر نفسه صحيح لأقمار زحل.
(جـ) الكواكب تتحرك في مدارات إهليلجية تكون الشمس في بؤرتها.
(د) متجه نصف القطر من الشمس إلى أي كوكب يمسح مساحات متساوية في أزمنة متساوية؛ أي إن معدل مسح المساحة ثابت.
(هـ) الأزمنة الدورية للكواكب، منسوبة لخلفية النجوم الثابتة، تتناسب مع متوسط أبعادها عن الشمس مرفوعًا إلى الأس 2/3. (البُعد «المتوسط» المشار إليه هنا هو متوسط أقرب وأبعد مسافتين يبعدهما الكوكب عن الشمس، ويساوي نصف المحور الأكبر للقطع الناقص.)
استنتج يوهانز كبلر (1571–1630) الحقائق (جـ) و(د) و(هـ) المعروفة على التوالي بقوانين كبلر الأول والثاني والثالث، وذلك من بيانات قدر كبير من الملاحظات.
من (د) أوضح نيوتن أن القوة المؤثرة على الكواكب تتجه نحو الشمس؛ أي إنها قوة مركزية. عند هذه النقطة نؤكد على أن (د) يدلنا على اتجاه القوة المؤثرة على الكواكب، ولكنه لا يقول شيئًا عن مقدار تلك القوة. واستنتج نيوتن من (جـ) و(هـ) أن مقدار القوة المؤثرة على كوكب ما يتناسب عكسيًّا مع مربع المسافة بين الكوكب والشمس، وطرديا مع قوة كتلة الكوكب.
بدلا من البحث في رياضيات صعبة نوعا ما وضرورية لوصف كوكب متحرك في مدار إهليلجي، دعنا نركّز على أقمار المشتري (الذي يتخذ مدارات دائرية). يتحرك قمر كتلته m في دائرة نصف قطرها R بسرعة مقدارها ثابت v وعجلة v2/R متجهة نحو مركز الدائرة ؛ لهذا توصل نيوتن إلى أن قوةً مقدارها:

يجب أن تجذب القمر نحو مركز المشتري. وفيما يتعلق «بالسبب» التفصيلي لتلك القوة فقد أفسح نيوتن مجالًا لبعض التحير، لكنه اعتبر بوضوح أن القوة مبذولة بطريقة ما بواسطة المشتري ذاته.
الزمن الدوري للقمر؛ أي الزمن اللازم لكي يدور دورة واحدة، هو:

وبهذا نستطيع إعادة كتابة المعادلة (30–3) على الصورة:

وحيث إن T تتناسب مع R3/2 (طبقا لـ (أ))، فإنه يمكننا أن نكتب:

معنى النتيجة الملاحظة (أ) أن ثابت التناسب k يكون له نفس القيمة لكل الأقمار؛ أي إن k لا يعتمد على كتلة القمر m.
بإدخال المعادلة (33–3) في المعادلة (32–3) وجد نيوتن أن:

أو بالكلمات:
القوة التي يؤثر بها المشتري على قمر كتلته m يبعد مسافة R عن مركز المشتري تتناسب مع m/R2 وتتجه نحو مركز المشتري.
وطبقًا لقانون نيوتن الثالث، يؤثّر القمر بقوة على المشتري. هذه القوة تتناسب كتلة مع M/R2؛ حيث M هي كتلة المشتري. بما أن القوة التي يؤثّر بها القمر على المشتري يجب أن تكون مساوية في المقدار (ومضادة في الاتجاه) للقوة التي يؤثّر بها المشتري على القمر، فإننا نرى أن القوة يجب أن تتناسب مع حاصل Mm (أي إن الثابت 4π2/k في المعادلة (34–3) يتناسب مع M)؛ وبناءً على ذلك يكون قانون القوة بين المشتري (كتلة M) والقمر (كتلة m) على بعد R من مركز المشتري هو:

حيث G ثابت (يسمى ثابت الجاذبية) لا يعتمد على m أو M.
من الواضح جليا أن هناك قوة جاذبة، أيضًا على صورة المعادلة (35–3)، بين زحل وكلٌّ من أقماره. فضلا عن ذلك، أوضح نيوتن أن قانونًا للقوة، بنفس هذه الصورة بين الشمس وكلٌّ من كواكبها، ضروري (وكاف) لتفسير قوانين كبلر. ومن المفترض احتمالا أن تؤثر الأرض بقوة مماثلة على قمرها الخاص. وعلى ما يبدو بوضوح من غايتنا المتاحة حاليًّا، كان مطلوبًا من نيوتن وثبة خيالية معتبرة ليعرف أن هذه القوة تتشابه في نوعها مع القوة التي تجذب بها الأرض تفاحة ساقطة من فرع شجرة. وقد تحقق أيضًا من أن هذه الفكرة يمكن اختبار صحتها عدديًّا. وكان أحسن من عبر عن عبقرية نيوتن في هذا الخصوص هو العالم الموسوعي الفرنسي بول فاليري: «على المرء أن يكون نيوتن آخر ليرى أن القمر يسقط بينما العالم كله يرى أنه لا يسقط.» 4
إذا رمزنا لكتلة الأرض بالرمز Me، فإن القوة التي تبذلها الأرض على كتلة m تبعد مسافة R عن مركز الأرض تكون GmMe/R2، وتكون عجلة الكتلة m نحو مركز الأرض هي GMe/R2 (لاحظ أن مقدار العجلة لا يعتمد على m)؛ بناءً على ذلك، عندما نقارن عجلة القمر amoon نحو الأرض مع العجلة g لتفاحة ساقطة عند سطح الأرض، أن تكون العجلتان بنسبة 2(Re/Rm)؛ حيث Re هو بعد التفاحة عن مركز يجب الأرض (أي إن Re هو نصف قطر الأرض)، وRm هو بعد القمر عن مركز الأرض. لقد علم نيوتن، في حدود جيدة للدقة، أن 60/1 Re/Rm =؛ وبهذا يكون
(Re/Rm)2 = 0.0002777. عجلة القمر هي v2/Rm، وسرعة القمر v هي
2πRm/T؛ حيث T الزمن الدوري لحركة القمر حول الأرض بإدخال 27.3 = T يومًا و108 × 3.844 = Rm أمتار،5 نحصل على v = 1023.97 m/s وv2/Rm = 0.002728 m/s، ونصل إلى أن amoon/g = 0.002728/9.8 = 0.0002783. لقد أجرى نيوتن هذا الحساب ووجده مقنعا بدون شك عندما قرنه بإثبات آخر لقانون تربيع القوة العكسي.
كان نيوتن مؤمنًا ببساطة وعالمية قوانين الطبيعة، وما دام قد انتهى إلى أن هناك قوة جاذبة موجودة بين المشتري وأقماره، وبين زحل وأقماره، وبين الأرض وقمرها، وبين الشمس والكواكب، فإنه افترض أن هناك قوة جذب مماثلة (سماها الجاذبية) موجودة بين أي جسمين. وأوضح أننا في ممارساتنا اليومية لا ندرك قوة التجاذب بين جسمين لأن القوة الجاذبة المتبادلة بينهما صغيرة للغاية مقارنةً بقوة الجاذبية التي تؤثر بها الأرض عليهما وافترض أن أي جسمين (جسمين صغيرين جدا) يتجاذبان بقوة مقدارها

تتجه من أحد الجسيمين إلى الآخر. في هذه المعادلة m و M هما كتلتا الجسيمين، وr المسافة بينهما.
السؤال الذي ينشأ على الفور هو: ما هي القوة التي تؤثّر بها كتلة كروية كبيرة (مثل الأرض) على جسيم ما؟ إذا كانت المسافة بين الجسيم ومركز الأرض كبيرة بالمقارنة مع نصف قطر الكرة، فسوف يكون هناك خطأ يمكن إهماله في استخدام المعادلة (36–3)، باعتبار أن r هي المسافة من مركز الكرة إلى الجسيم. لقد رأينا للتو أن هناك إثباتًا قويا لصحة المعادلة (36–3) حتى عندما تكون المسافة بين الجسيم ومركز الكرة غير كبيرة مقارنةً بنصف قطر الكرة (على سبيل المثال، اعتبر جسيمًا مثل تفاحة نيوتن وكرةً مثل الأرض)، مع اعتبار r هي المسافة بين مركز الكرة والجسيم.
أدرك نيوتن أنه إذا اعتبر المعادلة (36–3) بمنزلة قانون القوة الأساسي بين جسيمات، فإنه يكون من الممكن حساب القوة بين جسيم وتوزيع كتلة كروية، باعتبار التوزيع مؤلفًا من عناصر صغيرة عديدة (كلٌّ منها يؤثر على الجسيم بقوة تعطى بالمعادلة (36–3)؛ وجمع القوى التي تؤثر بها هذه العناصر على الجسيم. وتمنى لو يستطيع بيان أنه إذا كان الجسيم خارج توزيع الكتلة الكروية، تكون القوة هي نفسها كما لو كان توزيع الكتلة بأكمله قد تم استبداله بكتلة نقطية (لا نفس الكتلة الكلية) عند مركز الكرة. ويعتقد كثيرون أنه أرجأ نشر كتابه «المبادئ» عشرين سنة حتى أصبح لديه برهان مرض لهذه المسألة.
البرهان الوارد في كتاب «المبادئ» هندسي. وقد حذفنا البرهان هنا، لكن الطالب الملم بحساب التفاضل والتكامل ينبغي أن يكون قادرًا على إجراء الحساب. الفكرة هي أن تحلل توزيع الكتلة إلى عناصر صغيرة عديدة MΔ. القوة التي تؤثّر بها MΔ على جسیم كتلته m يكون مقدارها 2r/GmMΔ؛ حيث r المسافة بين MΔ وm؛ واتجاه هذه القوة على طول الخط الواصل بين MΔ وm. نوجد القوة الكلية على m عن طريق الجمع المتجهي لجميع القوى المؤثرة على m بواسطة عناصر الكتلة ΔM (يُستخدم التكامل لإجراء عملية جمع كل الإسهامات المتناهية في الصغر). استخدم نيوتن (الذي اخترع حساب التفاضل والتكامل، برغم أن جوتفرد ليبنز كان أول من نشر براهين كاملة) برهانا هندسيا بدلا من التكامل لكيلا يُرهق قُراءه أو يربكهم. ونحن من جانبنا نؤكد على أن البرهان (سواء أكان هندسيًّا أم بحساب التكامل يعتمد بشدة على حقيقة أن القوة بين جسيمات ما تتغير عكسيًا مع مربع المسافة. إذا كان الأس بخلاف 2، فلن تكون هي الحالة التي يُسفر فيها توزيع كتلة كروية عن نفس تأثير الجاذبية الذي تسببه كتلة نقطية موضوعة عند مركز الكرة.
ربما يقلق قارئ ماهر من مناقشتنا لحركة القمر حول الأرض، وحركة أقمار المشتري وزحل حول كوكبيها في كلٌّ من هذه الحالات استعملنا قانون نيوتن الثاني في إطار إسناد معرَّف بمحاور غير دوارة بالنسبة إلى نجوم ثابتة)، ونقطة أصله تتحرك مع مركز الكوكب المعني. مثل هذه المحاور ليست إطارا قصوريًا لأنها متعاجلة (متسارعة) بالنسبة إلى محاور غير دوّارة نقطة الأصل لها مثبتة في الشمس.
عجلة هذه المحاور غير القصورية غير قابلة للإهمال. على سبيل المثال، عجلة الأرض في حركتها الدائرية تقريبًا حول الشمس أكبر من ضعف عجلة القمر بالنسبة إلى الأرض (يمكن للقارئ التحقق باستخدام النسبة المعروفة لبعدَي الأرض عن الشمس والقمر، ونسبة الشهر إلى السنة). ومع ذلك فإن المناقشة ليست صحيحة؛ لأنه عندما طبقنا قانون نيوتن الثاني 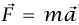 على القمر، كانت القوة الوحيدة التي اعتبرناها هي قوة الجاذبية التي تؤثر بها الأرض على القمر. وحذفنا اعتبار قوة الجاذبية التي تؤثر بها الشمس على القمر. ولدرجة عالية من الدقة، تؤثر الشمس بنفس القوة لوحدة الكُتل على القمر وعلى الأرض؛ لأن المسافة بين الأرض والقمر صغيرة جدًّا مقارنةً بالمسافة بين الأرض والشمس؛ لهذا فإن الشمس تُسبب نفس عجلة كل من الأرض والقمر، والعجلة النسبية لهما تُعزى فقط إلى قوتي الجاذبية المتبادلة بين الأرض والقمر. تطبق ملاحظات مماثلة على المشتري وأقماره وعلى زحل وأقماره.
على القمر، كانت القوة الوحيدة التي اعتبرناها هي قوة الجاذبية التي تؤثر بها الأرض على القمر. وحذفنا اعتبار قوة الجاذبية التي تؤثر بها الشمس على القمر. ولدرجة عالية من الدقة، تؤثر الشمس بنفس القوة لوحدة الكُتل على القمر وعلى الأرض؛ لأن المسافة بين الأرض والقمر صغيرة جدًّا مقارنةً بالمسافة بين الأرض والشمس؛ لهذا فإن الشمس تُسبب نفس عجلة كل من الأرض والقمر، والعجلة النسبية لهما تُعزى فقط إلى قوتي الجاذبية المتبادلة بين الأرض والقمر. تطبق ملاحظات مماثلة على المشتري وأقماره وعلى زحل وأقماره.
يصعب القياس المباشر لثابت التناسب G في معادلة قانون القوة (36–3) لأن قوة الجاذبية صغيرة جدا بالنسبة إلى قيم الكتل والمسافات التي يسهل الحصول عليها تجريبيا. كان كافندش في عام 1798 هو أول من حصل على تحديد دقيق للثابت G بالقياس المباشر للقوة بين كتلتين معلومتين تفصلهما مسافة معلومة.6 القيمة المقبولة اليوم هي G = 6.67384 × 10–11 m3 kg–1 s–2 = 6.67384 × 10–11 N–m2/kg27
وحيث إن العجلة g لجسم يسقط سقوطا حرا عند سطح الأرض تعطى بالمعادلة:

فإننا نستطيع حساب كتلة الأرض Me من قيم معلومة لكلِّ من g وG وRe، فيكون: Me = 5.97 × 1024 kg
استطاع نيوتن، قبل كافندش بقرن من الزمان، أن يقدم تقديرًا معقولا للثابت G، بتخمين الكثافة المتوسطة للأرض على أنها بين خمسة وستة أضعاف كثافة الماء («من المحتمل أن تكون كمية المادة الكلية للأرض أكبر منها خمسة أو ستة أضعاف إذا كانت كلها مكونة من ماء.»).8 من قيمة الكثافة المفترضة وقيمة Re المعلومة، حسب نيوتن Me، ثم G في حقيقة الأمر، كان تخمين نيوتن جيدًا بدرجة لافتة للنظر. الكثافة الحقيقية للأرض هي ضعف كثافة الماء 5.5 مرات.
مثال 3–14 (مدار قمر صناعي). قمر صناعي يدور حول الأرض في مسار دائري نصف قطره R. احسب الزمن الدوري T لهذا القمر.
(أ) أوجد قيمة T عندما يكون R = 1.05Re (وهو مقدار كبير لدرجة تكفي لحذف مقاومة الهواء).
(ب) أوجد نصف القطر R لمدار متزامن المدار المتزامن، الذي يُستخدم لأقمار الاتصالات، يضع القمر في مدار دائري في مستوى يشمل خط الاستواء، على ارتفاع يجعله دائمًا فوق نفس النقطة على الأرض مباشرةً.
القوة المؤثرة على القمر، والمتجهة نحو مركز الأرض، هي GmMe/R2. وعجلة القمر هي v2/R، وتتجه نحو مركز الأرض. فيكون GmMe/R2 = mv2/R. بإدخال
v = 2πR/T نجد أن:

حتى لو لم نعلم قيمتي G وMe فإننا نستطيع تعيين الطرف الأيمن للمعادلة (38–3) باستخدام المعادلة (37–3). نعيد كتابة المعادلة (38–3) على الصورة:

إذا كان 1.05 = R/Re، نجد أن 91 = T دقيقة. وبالنسبة إلى مدار متزامن نجد أن 23.9 = T 9 ساعة (الزمن الدوري لدوران الأرض بالنسبة إلى النجوم البعيدة مختلف، ويُعرف باليوم الشمسي)؛ وبهذا نجد أن 16.97 = 2/3(R/Re) و6.60 =R/Re على الطالب أن يحسب مقدار السرعة (بالأمتار لكل ثانية) لقمر صناعي في كلٌّ من هذين المدارين.
___________________________________________
هوامش
(4) Paul Valéry, Regards sur le monde actuel et autres essais, Paris: Gallimard, 5, rue Gaston-Gallimard, 75328 Paris cedex 07, 1945.
(5) NASA Staff, Solar system exploration — earth’s moon: Facts & figures, Retrieved 2012-09-29.
(6) A. Stanley Mackenzie Ph.D., The laws of gravitation: Memoirs by newton, bouguer and cavendish, American Book Company, PO Box 2638, Woodstock, GA 20188-1383, 1900.
(7) P. J. Mohr, B. N. Taylor, and D. B. Newell, the 2010 codata recommended values of the fundamental physical constants, National In situte of Standards and Technology, Gaithersburg, MD 20899.
(8) Isaac Newton, Principia Mathematica, Running Press Book Pub lishers, 125 South Twenty-second Street, Philadelphia, PA 19103-4399, 2002.
(9) S. Aoki, B. Guinot, G. H. Kaplan, H. Kinoshita, D. D. McCarthy, and P. K. Seidelmann, The new definition of universal time, Astronomy and Astrophysics 105(2) (1982), 361.



|
|
|
|
لصحة القلب والأمعاء.. 8 أطعمة لا غنى عنها
|
|
|
|
|
|
|
حل سحري لخلايا البيروفسكايت الشمسية.. يرفع كفاءتها إلى 26%
|
|
|
|
|
|
|
جامعة الكفيل تحتفي بذكرى ولادة الإمام محمد الجواد (عليه السلام)
|
|
|