المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | مربع كامل Complete Square |
 4735
 02:36 صباحاً
التاريخ: 13-12-2015 |
المؤلف : صالح رشيد بطارسه 
الكتاب أو المصدر : معجم الرياضيات 
الجزء والصفحة : 304|
أقرأ أيضاً
التاريخ: 15-11-2015
2170
التاريخ: 19-11-2015
1660
التاريخ: 29-10-2015
4123
التاريخ: 3-11-2015
10924
|
يرتبط المربع الكامل بالأعداد والمقادير الجبرية كما يلي :
للأعداد : هو العدد الحقيقي الذي جذره التربيعي عدد نسبي مثل
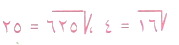
وهكذا .
وللمقادير الجبرية هو المقدار الجبري القابل للتحليل إلى العوامل إلى مقدارين متطابقين تماماً .
والذي يكون على الصورة س2 + 2 أ س + أ2 = (س + أ ) ( س + أ)
= ( س + أ)2
ومنها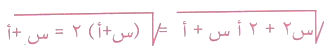 
وحتى تكون العبارة التربيعية كمقدار جبري مربع كامل يجب ان يكون
|
|
|
|
للعاملين في الليل.. حيلة صحية تجنبكم خطر هذا النوع من العمل
|
|
|
|
|
|
|
"ناسا" تحتفي برائد الفضاء السوفياتي يوري غاغارين
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|
