


 الفيزياء الكلاسيكية
الفيزياء الكلاسيكية
 الكهربائية والمغناطيسية
الكهربائية والمغناطيسية
 علم البصريات
علم البصريات
 الفيزياء الحديثة
الفيزياء الحديثة
 النظرية النسبية
النظرية النسبية
 الفيزياء النووية
الفيزياء النووية
 فيزياء الحالة الصلبة
فيزياء الحالة الصلبة
 الليزر
الليزر
 علم الفلك
علم الفلك
 المجموعة الشمسية
المجموعة الشمسية
 الطاقة البديلة
الطاقة البديلة
 الفيزياء والعلوم الأخرى
الفيزياء والعلوم الأخرى
 مواضيع عامة في الفيزياء
مواضيع عامة في الفيزياء|
Read More
Date: 10-2-2017
Date: 16-12-2015
Date: 16-12-2015
|
Classical Fields
First let us consider the evolution of a classical field in Rindler space. Can be described in a self-contained way. Obviously influences from Regions II and III can never be felt in Region since no point in Regions II or III is in the causal past of any point in Region I. Signals from Region IV can, of course, reach Region I, but to do so they must pass through the surface ω = −∞. Therefore signals from Region IV are regarded as initial data in the remote past by the Rindler observer. Evidently the Rindler observer sees a world in which physical phenomena can be described in a completely self-contained way.
The evolution from one surface of constant ω to another is governed by the Rindler Hamiltonian. Using conventional methods the generator of ω-translations is given by
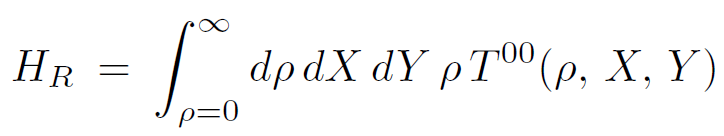 (1.1)
(1.1)
where T 00 is the usual Hamiltonian density used by the Minkowski observer. For example, for a massive scalar field with potential V , T 00 is given by
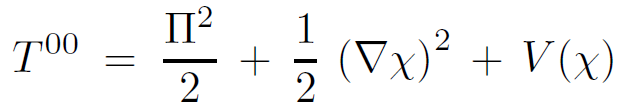 (1.2)
(1.2)
where Π is the canonical momentum conjugate to χ. The Rindler Hamiltonian is
 (1.3)
(1.3)
The origin of the factor ρ in the Rindler Hamiltonian density is straightforward. The relation between neighboring equal Rindler-time surfaces is shown. The proper time separation between the surfaces is
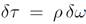 (1.4)
(1.4)
Thus, to push the ω-surface ahead requires a ρ-dependent time translation. This is the reason that T 00 is weighted with the factor ρ. The Rindler Hamiltonian is similar to the generator of Lorentz boosts from the viewpoint of the Minkowski observer. However it only involves the degrees of freedom in Region I.



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|