المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | نظرية فيثاغورس Pythagoras Theorem |
 3862
 01:54 صباحاً
التاريخ: 27-12-2015 |
المؤلف : صالح رشيد بطارسه 
الكتاب أو المصدر : معجم الرياضيات 
الجزء والصفحة : 362|
أقرأ أيضاً
التاريخ: 8-2-2017
1386
التاريخ: 13-2-2017
944
التاريخ: 12-2-2017
1201
التاريخ: 21-12-2015
4536
|
وضع فيثاغورس ( 572 – 497) ق.م أو تلاميذه من بعده ، نظريته المشهورة والمعروفة باسمه في القرن السادس قبل الميلاد ولا تزال للآن تدرس في مدارسنا والجامعات على السواء وتستخدم في حياتنا العملية في مجالات الأعمار والبناء.
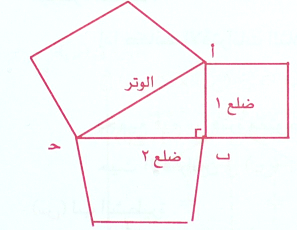
منطوقها العام يقول :
مساحة المربع المنشأ على وتر المثلث القائم الزاوية يكافئ مجموع مساحتي المربعين المنشأين على ضلعين الآخرين وبالرموز (أ جـ)2 = (أ ب)2 + (ب جـ)2
وهناك حالة خاصة للمثلث القائم الزاوية الذي زواياه 90 ْ ، 60 ْ ، 30 ْ كما في الشكل حيث الضلع المقابل للزاوية 30 يساوي نصف الوتر .
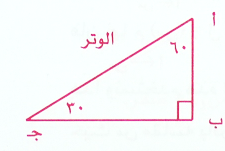
أي ان أب=12أجـ.
|
|
|
|
دراسة تحدد أفضل 4 وجبات صحية.. وأخطرها
|
|
|
|
|
|
|
جامعة الكفيل تحتفي بذكرى ولادة الإمام محمد الجواد (عليه السلام)
|
|
|
