


 الفيزياء الكلاسيكية
الفيزياء الكلاسيكية
 الكهربائية والمغناطيسية
الكهربائية والمغناطيسية
 علم البصريات
علم البصريات
 الفيزياء الحديثة
الفيزياء الحديثة
 النظرية النسبية
النظرية النسبية
 الفيزياء النووية
الفيزياء النووية
 فيزياء الحالة الصلبة
فيزياء الحالة الصلبة
 الليزر
الليزر
 علم الفلك
علم الفلك
 المجموعة الشمسية
المجموعة الشمسية
 الطاقة البديلة
الطاقة البديلة
 الفيزياء والعلوم الأخرى
الفيزياء والعلوم الأخرى
 مواضيع عامة في الفيزياء
مواضيع عامة في الفيزياء|
أقرأ أيضاً
التاريخ: 10-10-2020
التاريخ: 10-10-2020
التاريخ: 11-10-2020
التاريخ: 2024-01-13
|
التدفق المغناطيسي ( الفيض)
لقد فسر فاراداي القوة الدافعة الكهربية المستحثة في ملف ما بدلالة كمية تسمى التدفق المغناطيسي. ومن أجل هذا ، ابتكر قاعدة تحدد كيفية رسم خريطة لخطوط المجال المغناطيسي. فإذا كان للمجال المغناطيسي في منطقة ما مقدار هو B فإننا نمثل هذا المقدار بيانياً بأن نتفق على رسم خطوط المجال وهي على أبعاد معينة من بعضها البعض ، وأن تمثل المجالات الأضعف بخطوط متباعدة عن بعضها البعض بشكل أكبر. وبعبارة أخرى يمكن القول بأن كثافة خطوط المجال في الرسم تتناسب مع قيمة B.
ويمكننا قياس كثافة الخطوط هذه لو أقمنا سطحاً متعامداً مع الخطوط ثم قمنا بعد الخطوط التي تخترق وحدة المساحات من هذا السطح ؛ كما في الشكل (1)، حيث يمر ستة عشر خطاً من خطوط المجال خلال مساحة قدرها 1 m2. وقد نود أن نختار كثافة الخطوط هذه لتمثل شدة مجال مغناطيسي ولتكن 1 T مثلاً. ومن ثم فإن منطقة تمر بوحدة المساحات بها ثمانية خطوط ستمثل شدة مجال مقدارها النصف أي 0.5 T ، أما المنطقة التي بها 32 خطاً في المرت المربع فإنها تمثل مجالاً شدته 2T وهكذا. أي أن التمثيل البياني للمجال المغناطيسي هو ان B تتناسب مع كثافة خطوط الفيض ، او مع عدد خطوط المجال التي تعبر مساحة ما مقسوما على تلك المساحة.
ويؤدي هذا التفسير إلى اعتبار أن عدد الخطوط المارة خلال المسافة A يمثل المقدارB┴A وهذا هو ما يسمى الفيض ( التدفق) المغناطيسي خلال A ، وعادة ما يعبر عنه بالرمز Φ:
(1) الفيض المغناطيسي خلالB┴A = Φ = A
ومن الواضح أن وحدات SI للفيض المغناطيسي ستكونT.m2 ونختصر هذه الوحدة في اسم خاص هو الوبر weber (Wb). وهكذا.
1 Wb = 1 T.m2
أو بدلاً من ذلك 1 T = 1Wb/m2
وبسبب هذا التعبير الأخير فإن المجال المغناطيسي B يشار إليه أحياناً بأنه كثافة الفيض ( التدفق).
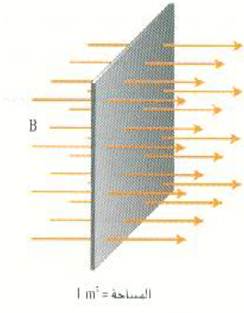
الشكل (1): سنتفق على رسم عدد خطوط المجال المغناطيسي بحيث يتناسب مع مقدار B ويخترق وحدة المساحات المتعامدة مع خطوط المجال.
ومن المهم جداً تذكر أننا اعتبرنا B متعامداً مع مستوى المساحة A في الشكل (2 أ) فإذا أدرنا المساحة A كما في الشكل (2 ب) فإنه لن تمر خلالها أية خطوط للمجال ولهذا فإن = 0Φ. وقد يكون الفيض سالباً كذلك كما هو موضح في الشكل (2 جـ) حيث يتخذ كل من B و n اتجاهين متضادين وهناك طريقة بسيطة لكتابة هذه العلاقة بين Φ والاتجاه وذلك بوصف اتجاه العمود n ، المقام على المساحة A. والمركبةB┴ = B cos θ هي مركبة B الموازية للعمود. وعلى هذا تكون المعادلة العامة للفيض المغناطيسي هي :
(2) Φ = (B cos θ)A = BA cos θ
حيث θ هي الزاوية المحصورة بين B وn.
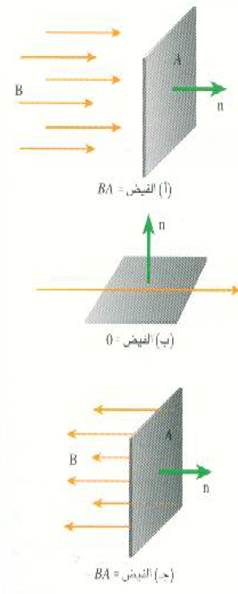
الشكل ((2: يعتمد الفيض خلال مساحة ما على الاتجاهات النسبية بين المساحة وخطوط المجال.



|
|
|
|
لصحة القلب والأمعاء.. 8 أطعمة لا غنى عنها
|
|
|
|
|
|
|
حل سحري لخلايا البيروفسكايت الشمسية.. يرفع كفاءتها إلى 26%
|
|
|
|
|
|
|
جامعة الكفيل تحتفي بذكرى ولادة الإمام محمد الجواد (عليه السلام)
|
|
|