


 الفيزياء الكلاسيكية
الفيزياء الكلاسيكية
 الكهربائية والمغناطيسية
الكهربائية والمغناطيسية
 علم البصريات
علم البصريات
 الفيزياء الحديثة
الفيزياء الحديثة
 النظرية النسبية
النظرية النسبية
 الفيزياء النووية
الفيزياء النووية
 فيزياء الحالة الصلبة
فيزياء الحالة الصلبة
 الليزر
الليزر
 علم الفلك
علم الفلك
 المجموعة الشمسية
المجموعة الشمسية
 الطاقة البديلة
الطاقة البديلة
 الفيزياء والعلوم الأخرى
الفيزياء والعلوم الأخرى
 مواضيع عامة في الفيزياء
مواضيع عامة في الفيزياء|
أقرأ أيضاً
التاريخ: 29-11-2020
التاريخ: 7-12-2016
التاريخ: 19-2-2016
التاريخ: 10-8-2017
|
الشغل وطاقة الحركة الدورانيان
من السهل أن نرى ان للجسم الدائر طاقة حركة. فالعجلة المبينة في الشكل ((1 مثلاً تتكون من قطع صغيرة من الكتلة يتحرك كل منها أثناء حركة العجلة. فأي جزء صغير من الكتلة، مثل الجزءm1 في الشكل، له سرعة قدرهاv1 ، وله بالتالي طاقة حركة تساوي1/2 m1 v21 . لنبدأ دراستنا لخواص الأجسام الدائرة بتحليل كيف يمكن ان تكتسب عجلة ما طاقة حركتها.

الشكل ((1
يمثل الشكل (2) عجلة ساكنة في البداية، ولكنها تستطيع الدوران بحرية حول محور دورانها الذي يمر بمركزها. عندما تؤثر قوة شد F على الخيط الملفوف على حافة العجلة تبدأ العجلة في الدوران. في هذه الحالة يعطى الشغل المبذول بواسطة القوة أثناء شد الخيط مسافة قدرها s بالمعادلة:
Fs = الشغل المبذول بواسطة F
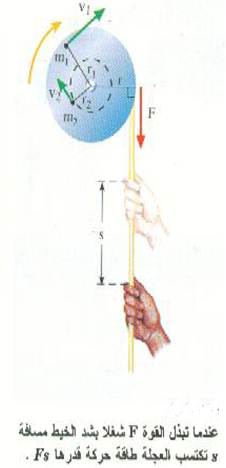
الشكل (2)
وبدوران العجلة زاوية قدرها θ ينفك من الخيط طول قدره s، حيث تمثل العلاقة بين s و θ بالمعادلةs = rθ . وبالتعويض عن s بهذه القيمة نصل إلى التعبير الآتي للشغل المبذول:
F rθ = الشغل المبذول بواسطة F
يمكننا فهم هذه العلاقة بصورة أفضل بملاحظة أن Fr هي " القوة المضروبة في ذراع الرافعة " في الشكل (2) ، وهذه الكمية ببساطة هي عزم الدوران T المؤثر على العجلة. ومن ثم نجد أن العلاقة بين الشغل المبذول على العجلة عندما تدور زاوية قدرها θ وعزم الدوران المؤثر عليها هي :
(1) W = Tθ
من المهم ملاحظة أن هذه هي النتيجة التي يمكن التوصل إليها تخميناً بالتناظر مع الحركة الخطية. ففي حالة الحركة الخطية نجد أنW = Fx x ، أما في حالة الدوران فإن القوة تستبدل بعزم الدوران، كما ان المسافة الخطية تستبدل بالمسافة الزاوية وعليه فإن Fx x في الحركة الدورانية تصبح Tθ في الحركة الدورانية ، كما أثبتنا في المعادلة (1).
طبقاً لنظرية الشغل والطاقة يجب أن يظهر الشغل المبذول بواسطة صافي القوة على العجلة في صورة طاقة حركة. وسوف تسمى طاقة حركة جسك دائر بطاقة الحركة الدورانيةKErot وربما تذكر أن طاقة حركة جسم بسبب حركته الخطية هي 1/2 mv2، وسوف يشار إلى هذه الطاقة فيما بعد باسم طاقة الحركة الانتقاليةKEtrans لنحاول الآن حساب طاقة حركة جسم دائر بالاستعانة بطاقة حركة كل من كتل الأجزاء الصغيرة المكونة للجسم.
لنعد مرة أخرى إلى الشكل (1). عندما تدور العجلة تكتسب كل كتلة دقيقة ( مثل m1) من الكتل المماثلة الكثيرة المكونة للجسم طاقة حركة انتقالية، وهذه تكون 1/2 m1 v21 للكتلة m1. وإذا اعتبرنا أن العجلة تتكون من عدد قدره Nمن الكتل الدقيقةm1 ،m2 ،m3 ،...mN المكونة للعجلة فإن طاقة حركتها الكلية تكون:
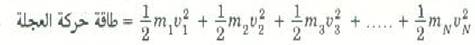
ولكنm1 مثلاً تتحرك في دائرة نصف قطرهاr1، وتكون سرعتها المماسية على هذه الدائرةv1 وحيث أن السرعة الزاوية للعجلة ترتبط بهذه السرعة المماسية طبقاً للمعادلةv1 = ωr1 ، فإن :
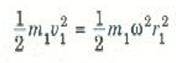
وبالمثل يمكننا استنتاج تعبيرات مشابهة لجميع الكتل الدقيقة الأخرى. إذن، بالتعويض عن هذه القيم في معادلة طاقة الحركة نحصل على:
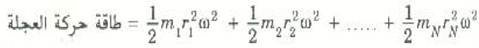
وحيث أن كل اجزاء العجلة تتحرك جميعها بنفس السرعة الزاوية ω، يمكننا إذن كتابة المعادلة السابقة على الصورة:

المقدار بين القوسين في العلاقة السابقة يسمى عزم القصور الذاتي للجسم الدائر ويرمز له عادة بالرمز I:
(2) 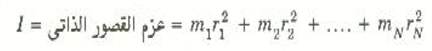
لاحظ أن وحدات I في النظام SI هيkg. m2 .
وعندئذ سنرى أنه حقيقة مقياس للقصور الذاتي للعجلة. ومع ذلك يمكننا أن نرى حتى في هذه اللحظة أنه يعتمد ليس فقط على كمية المادة m في الجسم، بل إنه يعتمد أيضاً على كيفية توزيع تلك المادة.
الآن يمكن كتابة تعبيرنا لطاقة حركة العجلة الدائرة بدلالة I :
(3) 
هذه هي طاقة حركة الجسم التي يكتسبها بسبب دورانه. لاحظ مرة ثانية أنه كان بإمكاننا تخمين الصورة العامة لطاقة الحركة الدورانية. وبالتماثل مع الكمية1/2mv2 فإن السرعة الخطية v قد استبدلت بالسرعة الدورانية ω وأن I هي المقابل الدوراني للكتلة m.
أن الطاقة الدورانية مرتبطة بالشغل المبذول على العجلة بواسطة عزم الدوران المؤثر عليها. ولكي نكون أكثر تحديداً، لنفرض أن العجلة دائرة بسرعة مقدارها 0ω ثم أثرنا عليها فجأة بعزم دوران معينT0 لنفرض أن تأثير عزم الدوران قد استمر أثناء دوران العجلة بزاوية θ ( بحيث كان الشغل المبذول بواسطة عزم الدوران Tθ) ثم أزيل عنها ، وأن السرعة الزاوية للعجلة في تلك اللحظة fω بتطبيق نظرية الشغل والطاقة على هذا الموقف نجد أن:
التغير في KE للعجلة = الشغل المبذول على العجلة
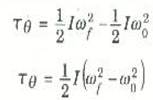
حيث استخدمنا المعادلة (1) للتعبير عن طاقة الحركة الدورانية للعجلة.
يمكن تبسيط هذه العلاقة بين الشغل وطاقة الحركة الدورانية باستخدام معادلة الحركة الزاوية: 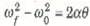 وبالتعويض عن هذه الكمية في معادلة الشغل والطاقة السابقة واختصار θ نحصل على:
وبالتعويض عن هذه الكمية في معادلة الشغل والطاقة السابقة واختصار θ نحصل على:
(4) T = I α
حيث a هي العجلة الزاوية مقدرة بالزوايا نصف القطرية لكل ثانية مربعة. بهذه الطريقة أمكننا الوصول إلى علاقة بين العجلة الزاوية لحركة العجلة وعزم الدوران المسبب لهذه العجلة. هذه المعادلة للحركة الدورانية تناظر المعادلة F= ma في حالة الحركة الخطية.



|
|
|
|
لصحة القلب والأمعاء.. 8 أطعمة لا غنى عنها
|
|
|
|
|
|
|
حل سحري لخلايا البيروفسكايت الشمسية.. يرفع كفاءتها إلى 26%
|
|
|
|
|
|
|
جامعة الكفيل تحتفي بذكرى ولادة الإمام محمد الجواد (عليه السلام)
|
|
|