


 الفيزياء الكلاسيكية
الفيزياء الكلاسيكية
 الكهربائية والمغناطيسية
الكهربائية والمغناطيسية
 علم البصريات
علم البصريات
 الفيزياء الحديثة
الفيزياء الحديثة
 النظرية النسبية
النظرية النسبية
 الفيزياء النووية
الفيزياء النووية
 فيزياء الحالة الصلبة
فيزياء الحالة الصلبة
 الليزر
الليزر
 علم الفلك
علم الفلك
 المجموعة الشمسية
المجموعة الشمسية
 الطاقة البديلة
الطاقة البديلة
 الفيزياء والعلوم الأخرى
الفيزياء والعلوم الأخرى
 مواضيع عامة في الفيزياء
مواضيع عامة في الفيزياء|
أقرأ أيضاً
التاريخ: 2024-03-08
التاريخ: 22-11-2020
التاريخ: 2-2-2016
التاريخ: 24-11-2020
|
قانون نيوتن للجاذبية
تعتبر حركة الكواكب حول الشمس واحدة من أهم امثلة الحركة في مسار شبه دائري، وكانت هذه الحركة موضوع دراسات دقيقة مستفيضة للكثير من العلماء قبل أربعة قرون. فمن العام 1576 وحتى 1597 قام الفلكي الدانماركي تايكو براهي Tycho Brahe بجمع وتصنيف ادق وأشمل النتائج المرصدية لحركة الكواكب في ذلك الحين على الإطلاق. وبناء على هذه النتائج استطاع يوهانز كبلرJohannes Kepler وضع قوانينه الشهيرة عن الحركة الكوكبية خلال الأعوام 1609 - 1618. هذه القوانين تبين أن المدارات الكوكبية دائرية تقريباً، وأن الزمن الذي يستغرقه الكوكب حول الشمس T يتناسب مع مكعب بعد الشمس R:
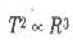
وتعرف العلاقة السابقة بقانون كبلر الثالث.
وعندما بدأ نيوتن دراسته للقوى في القرن السابع عشر كانت نتائج دراسات كبلر ومن سبقه عن الحركة الكوكبية متاحة له، ولكن القانون الفيزيائي الموحد الذي يفسر سلوك الكواكب لم يكن بعد معروفاً. وبمجرد ان تبلورت قوانين نيوتن للحركة، بما في ذلك مفهوم القوة والعجلة الجاذبتين المركزيتين ، أصبح الطريق واضحاً أمام نيوتن لاكتشاف طبيعة قوة الجاذبية.
وبناء على هذه القوانين استنتج نيوتن منطقياً ان هناك قوة تجاذبية بين الشمس وأي كوكب، وان هذه القوة تسبب العجلة الجاذبة المركزية اللازمة لدوران الكوكب في مداره. ومن ثم ، حيث أنFg = mac لكتابة:
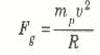
حيثmp كتلة الكوكب. كذل اهتدى نيوتن بالاستدلال المنطقي أن الزمن المداري او الدورة T يكون:

وبتربيع هذه العلاقة واستخدام قانون كبلر الثالث نحصل على:
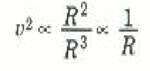
وبتجميع كل هذه العلاقات استنتج نيوتن أن القوة التي تؤثر بها الشمس على الكوكب يجب ان تكون على الصورة :

وباستخدام قانونه الثالث تحقق نيوتن ان الكوكب يؤثر على الشمس بقوة مساوية (شكل (1)) هذا التماثل يعني أن القوة يجب أن تعتمد على كلتا الكتلتين بنفس الطريقة، أي أن القوة يجب ان تكون على الصورة:
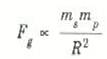
حيثms كتلة الشمس.
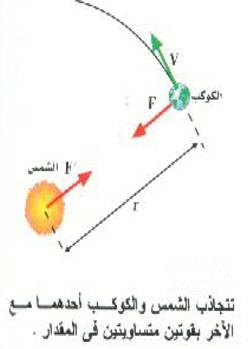
الشكل (1)
كذلك افترض نيوتن أن نفس الجاذبية التي تسبب تسارع القمر نحو الأرض (العجلة الجاذبة المركزية) تسبب أيضاً سقوط الأجسام (كالتفاحة الأسطورية في بستانه) تجاه الأرض بالعجلة g. ولاقتناعه أن قوة الجاذبية قوة كونية اساسية قام نيوتن بتعميم الأمثلة السابقة في قانونه العام للجاذبية:
إذا كانت المسافة بين مركزي كرتين منتظمتين كتلتاهماm1 وm2 هي r فإن كلاً من الكرتين تجذب الأخرى بقوة مقدارها:
(1) 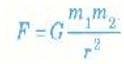
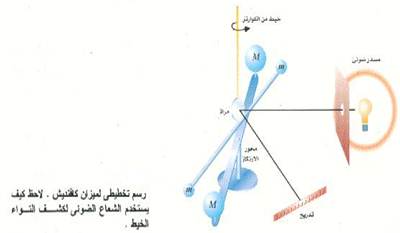
الشكل (2)
من الجدير بالذكر أن قيمة ثابت الجاذبية G لا يمكن تعيينها نظرياً، ولكن يمكن تعينها بالتجربة فقط. وقد كان هنري كافنديش Henry Cavendish اول من قام بإيجاد قيمته عام 1798 مستخدما جهازاً يسمى ميزان كافنديش (شكل (2)).
الكتلتان الصغيرتان المتماثلتان m في ميزان كافنديش معلقتان في خيط رفيع دقيق جداً من الكوارتز. عند تحريك الكتلتين الكبيرتين M بحيث تقتربان من الكتلتين الصغيرتين m سوف يسبب التجاذب بين M و m التواء الخيط. وبمعايرة الجهاز بحيث تعرف القوة اللازمة لحدوث التواء معين يمكن حساب قوة التجاذب بين m و M مباشرة من قيمة التواء الخيط المقاسة. وحيث أن F، r، M، m معلومة جميعها، يمكن إذن التعويض عن قيمتها في المعادلة (1) ثم حلها بالنسبة إلى مجهول الوحيد G. وطبقاً لأدق القياسات المتاحة في الوقت الحاضر فإن القيمة المقبولة حالياً لثابت الجاذبية G. وطبقاً لأدق القياسات المتاحة في الوقت الحاضر فإن القيمة المقبولة حالياً لثابت الجاذبية G هي:
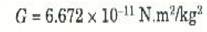



|
|
|
|
للعاملين في الليل.. حيلة صحية تجنبكم خطر هذا النوع من العمل
|
|
|
|
|
|
|
"ناسا" تحتفي برائد الفضاء السوفياتي يوري غاغارين
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|