


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 6-1-2016
Date: 15-10-2021
Date: 29-8-2021
|
In this short chapter we examine another aspect of compounding, in which either the compounding period is very short or the number of periods is very great. Again you may wish to have a calculator that enables you to raise numbers to integer powers while studying this section. It is also useful to have the constant e available on your calculator.
Continuous Compounding
In some cases, compounding takes place after a very short interval. For example, in some bank accounts, interest is calculated every day. Over 1 year, there are 365 compounding periods. (We saw earlier that the interest rate differs very little between the final interest if the standard year is used instead of the exact year.)
In other cases, even though the period is longer, there are still a large number of compounding periods. For example, suppose a company invests some of its funds and loses track of the investment for 100 years. It is found that there is little difference whether compounding took place monthly or quarterly.
For our calculations it will be convenient to work in terms of the fraction r =R/100 rather than the percentage R. If your bank applies interest to your account n times per year, the interest is R% and your initial investment (“capital”) was $A, then your ending capital after N years is
$A(1+r/n) nN.
Consider the example of 100% interest, the case r = 1. The following table shows the values of (1+1/n)n and (1+1/n)n −1 for several values of n. The right-hand number is the APY corresponding to an APR of 100% with compounding n times annually.
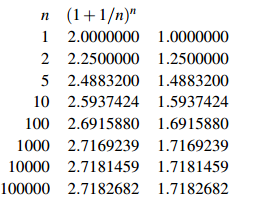
Eventually the right-hand number gets very close to a fixed value, usually denoted e, about 2.7182818...
A similar calculation can be made for other values of r. For large n, (1 + r/n)n gets very close to er. For example, if r = .1, then er = 1.105171.... Look at the result when we calculate (1+r/n)n for various values of n:
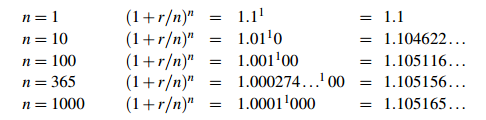
We define continuous compounding to be a process where, if your original capital is $P, then after N years, the ending capital is
$PerN.
The calculation above, case n = 365, shows that continuous compounding is a good approximation to daily interest, and many lenders use it instead of daily interest because it is easy to calculate.
Sample Problem 1.1 You borrow $50,000 at 10% annual interest, compounded continuously, for 10 years. Assuming you make no payments until the end of the period, how much will you owe (to the nearest dollar)?
Solution. We have P = 50,000, R = 10 and N = 10. So r = .1 and
PerN = 50,000×e = 135,914.09...
and you owe $135,914. Compare this with the result of Sample Problem 1.2in(Interest Periods), where compounding was quarterly and the answer was $134,253. The difference is not great.
The calculations involved in continuous compounding are closely related to natural logarithms. The logarithm to base b of a number x, written logb(x), is that number n such that bn = x. For example, logb(b) = 1,logb(b2) = 2, etc. If bn = x and bm = y, then xy = bn+m, so logarithms can be used to simplify arithmetic: in order to multiply two numbers, you add their logarithms. The most commonly used logarithms are to base 10; if you know that log10(2) = 0.3010..., then 20 = 10×2 so log10(20) = log10(10) + log10(2) = 1.3010...,log10(200) = 2.3010..., and so on. If we just write log(x) it is assumed that the base is 10. A natural logarithm is a logarithm to base e. (The natural logarithm function, written ln, is available on most scientific calculators.)
One advantage of continuous compounding is that one can easily calculate the interest when principal and interest rate are known. For example, suppose you invest $100 for 2 years and receive $21 interest. Your money grew from $100 to $121 with continuous compounding, so the rate r satisfied 100e2r = 121, so e2r = 1.21 and er = √1.21 = 1.1. From this, r will equal loge(1.1), which equals .0953..., so the interest rate was 9.53%.
The natural logarithm function, written ln, is available on most scientific calculators. However, you will seldom need to look it up. You don’t even need to calculate the value of r in order to find the interest; all you need is er . In the example, after n years, your capital will be $100 × (1.1)n and your interest will be $100 × [(1.1)n − 1]. Of course, you can easily calculate the APY—in the example, your money would grow from $100 to $110 in the first year, so the APY is 10%.
If you don’t want to deal with natural logarithms, there are tables to calculate the value of R (and r) from the APY.
Sample Problem 1.2 You borrow $50,000 at continuous compounding for 10 years. At the end of the period, you owe $100,000. What was the approximate APY?
Solution. Suppose the rate is r. Then 50,000e10r = 100,000 so e10r = 2.
Therefore er equals the tenth root of 2, which equals 1.0718 approximately. The amount owed at the end of 1 year—principal plus 1 year’s interest—is about 1.0718 times the principal. So the APY is approximately 0.0718, or 7.18%.
Observe that the figures of $50,000 and $100,000 were not an essential part of the above Sample Problem. The main point was the ratio: the debt at the end was double the principal. The answer would be the same for any value of P, provided the final amount owed was twice P.
If k is any constant, the function f(x) = kx is called an exponential function, and the situation where a quantity changes over x units of time from A to Akx is called exponential growth; x is the exponent. So continuous compounding is an example of exponential growth.



|
|
|
|
لصحة القلب والأمعاء.. 8 أطعمة لا غنى عنها
|
|
|
|
|
|
|
حل سحري لخلايا البيروفسكايت الشمسية.. يرفع كفاءتها إلى 26%
|
|
|
|
|
|
|
جامعة الكفيل تحتفي بذكرى ولادة الإمام محمد الجواد (عليه السلام)
|
|
|