

تاريخ الرياضيات

الاعداد و نظريتها

تاريخ التحليل

تار يخ الجبر

الهندسة و التبلوجي


الرياضيات في الحضارات المختلفة

العربية

اليونانية

البابلية

الصينية

المايا

المصرية

الهندية


الرياضيات المتقطعة

المنطق

اسس الرياضيات

فلسفة الرياضيات

مواضيع عامة في المنطق


الجبر

الجبر الخطي

الجبر المجرد

الجبر البولياني

مواضيع عامة في الجبر

الضبابية

نظرية المجموعات

نظرية الزمر

نظرية الحلقات والحقول

نظرية الاعداد

نظرية الفئات

حساب المتجهات

المتتاليات-المتسلسلات

المصفوفات و نظريتها

المثلثات


الهندسة

الهندسة المستوية

الهندسة غير المستوية

مواضيع عامة في الهندسة

التفاضل و التكامل


المعادلات التفاضلية و التكاملية

معادلات تفاضلية

معادلات تكاملية

مواضيع عامة في المعادلات


التحليل

التحليل العددي

التحليل العقدي

التحليل الدالي

مواضيع عامة في التحليل

التحليل الحقيقي

التبلوجيا

نظرية الالعاب

الاحتمالات و الاحصاء

نظرية التحكم

بحوث العمليات

نظرية الكم

الشفرات

الرياضيات التطبيقية

نظريات ومبرهنات


علماء الرياضيات

500AD

500-1499

1000to1499

1500to1599

1600to1649

1650to1699

1700to1749

1750to1779

1780to1799

1800to1819

1820to1829

1830to1839

1840to1849

1850to1859

1860to1864

1865to1869

1870to1874

1875to1879

1880to1884

1885to1889

1890to1894

1895to1899

1900to1904

1905to1909

1910to1914

1915to1919

1920to1924

1925to1929

1930to1939

1940to the present

علماء الرياضيات

الرياضيات في العلوم الاخرى

بحوث و اطاريح جامعية

هل تعلم

طرائق التدريس

الرياضيات العامة

نظرية البيان
Interpreting Samples
المؤلف:
W.D. Wallis
المصدر:
Mathematics in the Real World
الجزء والصفحة:
69-72
15-2-2016
2493
The main reason for sampling is to get an idea of the properties of the whole population. For example, if we want to know the mean of a population, our best guess is the mean of a representative sample, and similarly for the median. Naturally, a bigger sample will lead to a more reliable estimate.
Measures of spread in a sample can be used to estimate the spread of a population, but be careful! When you calculate the standard deviation of a sample, you use deviations from the mean of the sample, not the population. The sample mean is the best estimate of the population mean, but it is not perfect. The best estimate of the population mean would be made by using the squared deviations from the population mean, not the sample mean; but in most cases this is not available. When the population mean is not known, it can be shown that the best estimate of the population variance is found by summing the squared deviations from the sample mean, and then dividing by n − 1, where n is the sample size.
Usually we write m for the sample mean, and s for the estimate of the standard deviation found by dividing the sum of the squared deviations from m by n−1.
That is, if the readings in a sample are x1,x2,...,xn, then the sample standard deviation is
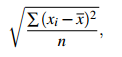
but the best estimate of the population standard deviation is
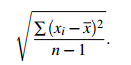
To get a 95% confidence interval for the mean of a normal (or approximately normal) population (such as human attributes like height and weight, or family incomes for large groups like cities), one takes a sample—let’s say its mean is x-—and use
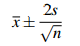
where, if the population standard deviation is known, σ say, we use s = σ; but if the population standard deviation is not known, we use

Sample Problem 1.1 You observe the output of a machine for 4 h. The machine produces the following number of screws per hour:
hour 1 : 20,050screws
hour 2 : 19,990screws
hour 3 : 20,020screws
hour 4 : 19,980screws.
Assuming these are typical hours of production, and assuming the hourly production follows approximately a normal distribution, find a 95% confidence interval for hourly screw production.
Solution. The mean is
(20,050+19,990+20,020+19,980)/4= 20,010.
The sum of squared deviations is
402+202+102+302= 3,000.
So the standard deviation estimate is
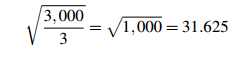
and the 95% range is
20,010±63.25.
In any kind of sampling, it is important to avoid bias, if we want to use the results to make predictions about the whole population.
Perhaps the most common type of bias in sampling is the convenience sample.
For example, an interviewer might wait outside a supermarket door and ask customers a question as they arrive. The customers at a supermarket might not be representative of the whole population. Another example is the telephone survey, which is biased toward those who have their telephones handy.
Another example of bias is self-selection. We have all seen surveys in newspapers and on television where the public are invited to respond. This type of survey will over-represent those who feel strongly about the topic. Another form of selfselection is when opinions are sought from a sample but only those who choose to respond are counted. This is called a voluntary response sample.
Sometimes the survey itself is biased. The question itself might suggest an answer.
A common form of sampling is an observational study. These are often conducted to test drugs, production methods, and so on. For example, to test whether too much chocolate increases the chance of diabetes, 100 rats were fed one pound of chocolate a day for 6 months. Fifteen percent developed diabetes, while the percentage among rats is only 3%. This does not prove that too much chocolate causes diabetes; other factors might be the increased calories in the diet, lack of exercise, laboratory conditions, and so on. This interference from other factors is called confounding.
Sample Problem 1.2 A sociologist wants to know the opinions of employed adult women about government funding for day care. She obtains a list of the 520 members of a local business and professional women’s club and mails a questionnaire to 100 of these women selected at random. Only 48 questionnaires are returned. What are the population and the sample in this survey? Is this survey biased?
Solution. The population is all employed adult women in the area represented by the club, and the sample is the set of 100 women randomly chosen. The study is almost certainly biased; business and professional women are not representative of all employed women, and the fact that only those who chose to respond are included will very probably affect the result.
To avoid confounding, a comparative study, also called an experimental study, is usually conducted. In this case other factors are controlled. The experimental subjects are divided into two groups, the experimental group and the control group.
Both groups receive exactly the same treatment except for the variable being tested.
For example, in the rat experiment, one could use 200 rats instead of 100. The original set of rats is the experimental group, while the new 100 are the control group. Other factors (laboratory conditions, calorie intake) are the same for the two groups; only the one variable—the amount of chocolate—varies between the two groups.
This technique works well when testing inanimate objects, or rats, but what if the experimental subjects are people? For example, suppose a new drug is being tested.
The very fact that you know you are receiving a drug, or that you know there is a new drug available and you are not receiving it, could influence your reaction.
For this reason, placebos are used. A placebo is a fake drug, looking exactly the same as the actual drug but not containing the active ingredient. For example, if the tablets used in an experiment contain 5 g of a new hormone substitute, the
placebo might instead contain 5 g of sugar. (This is a common example, and even if sugar and salt are not involved, placebo drugs are often called “sugar pills” or “salt pills.”) Subjects in medical experiments have a tendency to respond favorably to any treatment, whether the real one or the placebo; this is called the “placebo effect.”
In experiments involving placebos, it is standard practice that neither the participants nor those who test for effects are told which treatment was received.
In particular, if the subject is being interviewed about the effect of treatment, an interviewer who knew the difference might ask different questions depending on whether the subject received the test treatment or the placebo. The way to avoid this is for the interviewer not to know whether or not the particular subject is in the control group. Tests conducted in this way are called double blind.
 الاكثر قراءة في الاحتمالات و الاحصاء
الاكثر قراءة في الاحتمالات و الاحصاء
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















