


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 7-1-2016
Date: 7-1-2016
Date: 4-1-2016
|
We shall now look at the mathematics of finance: interest, investments, and loans.
In our brief overview we can only touch on a few elementary topics. Even for this, a calculator will be essential. In all our financial calculations, we use the idea of percentages. Recall that “percent” means “out of 100.” Therefore R% is just another way of saying R /100 .
In this chapter we shall introduce simple and compound interest.
Simple Interest
The idea of simple interest is well-known. Suppose you put $100 in a bank account, and at the end of 1 year the bank pays you back your $100 plus $6. This is called interest on your investment, and the rate is 6%.
This interest rate is always stated in terms of the annual interest. Suppose you put your $100 in the bank for 3 months, and receive $1.50 in interest. This is 1.5% of your original investment, but the rate is still quoted as 6%, the equivalent rate if the money had been kept for a year. To avoid confusion, it would sometimes be called “6% per annum” (“annum is Latin for “year”).
Sometimes you reinvest your money; in the first example, you would have $106 in your account at the beginning of year 2. If this process is carried out automatically by the bank, it is called compounding. We shall discuss compounding, and compound interest, in the next section. Simple interest is just the case where compounding does not occur. The obvious model is where you take out the interest and spend it, as for example when somebody retires and lives on the interest from their savings. If your investment pays simple interest, and you reinvest the interest rather than spending it, this is essentially the same as compounding.
The arithmetic of borrowing money (loans, mortgages) is similar to that for investing. Typically, you do not wait until the end of a loan period to pay back a loan. The usual practice is to pay equal amounts each month (or each week or . . . ).
For this reason, most loans involve compound interest. However, some loans use simple interest. We shall give examples at the end of this section.
The original amount you borrow is called the principal, or present value of an investment or loan. Suppose you draw simple interest on a principal $P for n years at R$ interest. The total amount you would receive is $A, where
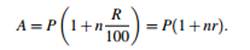
(where r is the fraction r = R/100); sometimes r is more convenient to use). The total interest is $I, where
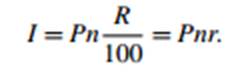
(We shall refer to these two equations as the “first simple interest formula” and the “second simple interest formula.”)
When dealing in periods shorter than a year, it is common to calculate as though the year consisted of 12 months, each of 30 days. This 360-day “year” is called a “standard” year. The regular 365-day year is called an “exact” year. Simple interest may be calculated for part of a year—n need not be an integer—and in that case, standard years are normally used.
In the case of an investment, simple interest is usually paid at the end of each year, but sometimes at the end of the loan period; for a loan, both interest and principal are typically paid at the end of the whole loan period. (Compound interest is normally used in cases where parts are paid throughout the loan period.)
Sample Problem 1.1 You borrow $1,600 at 12% simple interest for 4 months.
How much must you pay at the end of the period? How much would you pay if the loan were for 2 years?
Solution. We use the formula A = P(1 + nR/100) with P = 1,600 and R = 12.
In the first case, n is 1/3 (4 months is one-third of a year), so
A = 1,600×(1+.12/3) = 1,600×(1.04) = 1,664
and you repay $1,664. In the second case, n is 2, so
A = 1,600×(1+.12×2) = 1,600×(1.24) = 1,984
and you repay $1,984.
Using the “Simple Interest” Formulas
The first simple interest formula can be rewritten to make P the subject: given the final amount, interest rate and term, you can calculate the principal:
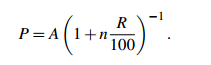
Similarly you can calculate the interest rate from the other data.
Sample Problem 1.2 You borrow $1,800 at simple interest for 6 months. At the end of the period you owe $1,863, including the principal. What was the interest rate?
Solution. Again we use A = P(1 + nR/100). We know A = 1,863, P = 1,800 and n = 1/2 . So
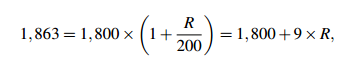
and therefore 9×R = 63,R = 7. So the interest rate was 7%.
Sample Problem 1.3 You need to borrow some money for 3 months. Your lender offers a rate of 12%. At the end of the period you repay $824. How much was the principal?
Solution. Using the formula with R = 12 and n = 1/4 , we get
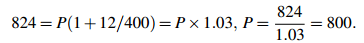
The principal was $800.
Sample Problem 1.4 You borrow $1,400 at simple interest for 3 years.
At the end of that period, your interest is $210. What was the interest rate?
Solution. In this case P = 1,400, I = 210 and n = 3. So, using the second simple interest formula,
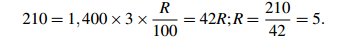
The rate was 5%.



|
|
|
|
دراسة تحدد أفضل 4 وجبات صحية.. وأخطرها
|
|
|
|
|
|
|
جامعة الكفيل تحتفي بذكرى ولادة الإمام محمد الجواد (عليه السلام)
|
|
|