


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 7-1-2016
Date: 23-2-2022
Date: 6-1-2016
|
Very often a bank pays interest more frequently than once a year. Say you invest at R% per annum for 1 year but interest is paid four times per year. The bank pays R /4 % every 3 months; this is called the interest period, or term. (Unfortunately, term is also used to denote the life of the loan.) If you invest $A, your capital after a year is
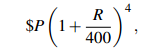
just as if the interest rate was divided by 4 and the number of years was multiplied by 4.
(Notice that we used the simplifying assumption that 3 months is a quarter of a year. In fact some quarters can be 92 days, others 91 or 90, but banks seldom take this into account. Similarly, when interest is calculated every month, it is usual to assume that each month is one-twelfth of a year.)
Sample Problem 1.1 Say your bank pays R = 8% annual interest, and interest is paid four times per year. What interest rate, compounded annually, would give you the same return?
Solution.(1+ R/400 )4 = (1.02)4 = 1.0824... so the effect is the same as compounding annually with 8.24...% interest rate.
Say interest is added t times per year. The result after 1 year is the same as if the interest rate were (R/t)% and the investment had been held for t years: after 1 year,
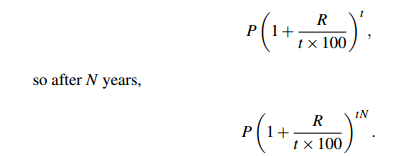
The calculations are exactly the same when you borrow money as they are when you invest money.
Sample Problem 1.2 You borrow $50,000 at 10% annual interest, compounded every 3 months, for 10 years. Assuming you make no payments until the end of the period, how much will you owe (to the nearest dollar)?
Solution. We have P = 50,000, R = 10, t = 4 and N = 10. So

which comes to 134,253.19... and you owe $134,253.
In Sample Problem 1.1, 8% is called the nominal rate of interest. The nominal rate doesn’t tell you how often compounding takes place. 8.24. . . % per annum is the effective rate. (These terms are established in the Truth in Savings Act.)
Sometimes banks and other lenders will talk about nominal rates per month or per quarter, but we shall always use these terms for the annual rates unless we specify otherwise.
When discussing a loan, the annual nominal rate is also called the annual percentage rate or APR. The yearly effective rate is called the annual percentage yield (APY) or effective annual rate (EAR). To avoid confusion, we shall refer to the APY, both for investments and loans.
Banks and other lenders like to tell you the APR, but what you really want to know is the APY. To calculate the APY, one works out how much would be owed on $100 at the end of a year, if no payments were made. This is not a real-world calculation: credit card companies and mortgage-holders normally require some minimum payment, or a penalty is charged. In calculating the APY, act as though all penalties are waived.
Sample Problem 1.3 Your credit card company charges an APR of 18%.
Payments are required monthly, and interest is charged each month. What is the corresponding APY?
Solution. The amount owing from a $100 loan at the end of 1 year is
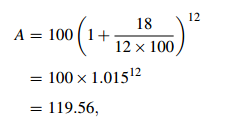
so the APY is 19.56%.
We said earlier that it is usual to use the 360-day “standard” year instead of the more accurate 365-day model. To conclude this chapter we show that this does not make a great deal of difference. Suppose you were to borrow money at the rate of 5%, compounded daily. If a 360-day year is used, the APY is

or 5.12677...%. If you borrow $10,000 and repay your loan after a year, you will owe between $10,512.67 and $10,512.68. The difference is less than one cent. And, in the real world, your debt would probably be rounded to the nearest dollar.



|
|
|
|
للعاملين في الليل.. حيلة صحية تجنبكم خطر هذا النوع من العمل
|
|
|
|
|
|
|
"ناسا" تحتفي برائد الفضاء السوفياتي يوري غاغارين
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|