


 الفيزياء الكلاسيكية
الفيزياء الكلاسيكية
 الكهربائية والمغناطيسية
الكهربائية والمغناطيسية
 علم البصريات
علم البصريات
 الفيزياء الحديثة
الفيزياء الحديثة
 النظرية النسبية
النظرية النسبية
 الفيزياء النووية
الفيزياء النووية
 فيزياء الحالة الصلبة
فيزياء الحالة الصلبة
 الليزر
الليزر
 علم الفلك
علم الفلك
 المجموعة الشمسية
المجموعة الشمسية
 الطاقة البديلة
الطاقة البديلة
 الفيزياء والعلوم الأخرى
الفيزياء والعلوم الأخرى
 مواضيع عامة في الفيزياء
مواضيع عامة في الفيزياء|
أقرأ أيضاً
التاريخ: 8-2-2016
التاريخ: 7-12-2016
التاريخ: 19-2-2016
التاريخ: 10-2-2016
|
الحركة الدورانية غير المنتظمة ( Non – uniform circular Motion)
وتمثل حركة جسم يدور بسرعة متغيرة كدالة للزمن وبذلك فإن الجسم سوف يكتسب نوعان من التسارع، الأول تساع خطي والثاني تسارع مركزي، ولذلك فسوف تتولد قوتان تؤثران على الجسم، الاولى قوة خطية مماسية للحركة FT والثانية قوة مركزية نحو مركز الدائرة Fr وكما في الشكل (1-1) حيث يمكن القول أن متجه القوة المحصلة المؤثرة على الجسم تساوي:
F = FT + Fr
وكذلك سوف يتولد نوعان من التسارع أحدهما خطي (aT) والآخر مركزي (ar) حيث:
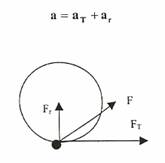
الشكل (1-1)
ولنفترض وجود جسم كتلته (m) معلق بصرف حبل طوله (r) وجعل الجسم يدور بسرعة متغيرة حول مركز الدوران كما في الشكل (1.2). لإيجاد قيمة الشد في الحبل وقيمة تسارع الجسم المماسي، نقوم بتحليل القوى المؤثرة على الجسم حيث:
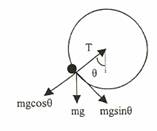
الشكل (1-2)
يؤثر وزن الجسم (mg) إلى الأسفل (نحو مركز الأرض)، وحيث أن الجسم يميل عند المحور الصادي بزاوية (θ)، إذا يمكن تحليل الوزن إلى مركبتان، إحداهما مماسية للحركة والاخرى عمودية للحركة حيث:
المركبة المماسية للوزن: mg sin θ
المركبة العمودية للوزن: mg cos θ
وفي المقابل فإن الشد في الحبل (T) يمثل القوة التي تجذب الجسم نحو مركز الدوران، إذا القوة المركزية التي تتولد من الحركة الدورانية ستساوي محصلة القوى باتجاه مركز الدائرة حيث:

تمثل المعادلة (1) مقدار الشد في الحبل الذي يعتمد فقط على قيمة الزاوية (θ). وكذلك فإن المركبة المماسية للوزن تمثل القوة الوحيدة بالاتجاه المماسي ، إذا:
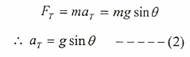
تمثل المعادلة (2) مقدار التسارع المماسي للجسم، ويلاحظ أنه كذلك يعتمد على زاوية الميل عن المحور الصادي (θ).
ومن الممكن دراسة حالتان للمعادلتين (1) ، (2) وهما:
1) عند أعلى نقطة في المسار الدائري حيث θ = 180o
وبالتعويض في المعادلة (1) نحصل على:

وهو يمثل أقل شد في الحبل يمكن أن يتولد أثناء الحركة.
وبالتعويض في المعادلة (2) نحصل على:
aT = 0
وهو قيمة تسارع الجسم المماسي في تلك النقطة.
2) عند أوطئ نقطة في السمار الدائري حيث θ = 0o
وبالتعويض في المعادلة (1) نحصل على:
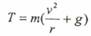
وهذا يمثل أكبر شد في الحبل يتولد من الحركة.
وبالتعويض بالمعادلة (2) نحصل على:
aT = 0
ويمثل تسارع الجسم المماسي في تلك النقطة.
ومن هذا نستنتج أن تسارع الجسم المماسي عند أعلى وأوطئ نقطة في المسار تساوي صفراً، اما عند الاماكن الاخرى في المسار فيتم حساب التسارع المماس من المعادلة (2) وبالتعويض عن قيمة زاوية ميل الجسم عند المحور الصادي.



|
|
|
|
دراسة تحدد أفضل 4 وجبات صحية.. وأخطرها
|
|
|
|
|
|
|
جامعة الكفيل تحتفي بذكرى ولادة الإمام محمد الجواد (عليه السلام)
|
|
|