


 الفيزياء الكلاسيكية
الفيزياء الكلاسيكية
 الكهربائية والمغناطيسية
الكهربائية والمغناطيسية
 علم البصريات
علم البصريات
 الفيزياء الحديثة
الفيزياء الحديثة
 النظرية النسبية
النظرية النسبية
 الفيزياء النووية
الفيزياء النووية
 فيزياء الحالة الصلبة
فيزياء الحالة الصلبة
 الليزر
الليزر
 علم الفلك
علم الفلك
 المجموعة الشمسية
المجموعة الشمسية
 الطاقة البديلة
الطاقة البديلة
 الفيزياء والعلوم الأخرى
الفيزياء والعلوم الأخرى
 مواضيع عامة في الفيزياء
مواضيع عامة في الفيزياء| القوى المحتفظة وغير المحتفظة (Conservative and Non - Conservative Force) |
|
|
|
أقرأ أيضاً
التاريخ: 14-3-2021
التاريخ: 2024-09-05
التاريخ: 29-12-2016
التاريخ: 2024-01-29
|
القوى المحتفظة وغير المحتفظة (Conservative and Non - Conservative Force)
تصنف القوى من حيث إمكانية حفاظها لقيمتها أو اضمحلالها خلال تأثيرها على الاجسام إلى نوعين:
1-1- القوى المحتفظة:
وهي تلك القوى التي تحافظ على قيمتها أثناء تأثيرها على الاجسام ويمكن استرجاع الشغل الناتج عنها دون نقص بعد انقضاء الحدث ، مثل قوى الجاذبية الأرضية.
ومن ميزات هذا النوع من القوى أن الشغل المبذول من قبلها على الأجسام لا يعتمد على طبيعة المسار الذي يسلكه الجسم بل يعتمد على إحداثيات النقطتان اللتان يتحركان بينهما الجسم، كما يتضح ذلك من الشكل (1-1) حيث يمكن القول أن الشغل المبذول خلال المسار (1) يساوي الشغل المبذول خلال المسار (2):

الشكل ((1-1
وفي حالة حركة الجسم من النقطة (p) إلى النقطة (َQ) ومن ثم العودة من نقطة (Q) إلى نقطة (p) فإن الشغل الكلي لمثل هذه الحلقة المغلقة من المسار يساوي صفراً حيث أن الشغل في المسار الأول يساوي سالب الشغل في المسار الثاني:
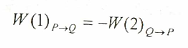
ومن الأمثلة العملية على الشغل الناتج من قوة الجاذبية الأرضية عند رفع جسم إلى ارتفاع (yi) ثم تركه يسقط باتجاه الأرض إلى ارتفاع ثاني هو (yf) وكما موضح في الشكل (1-2).

الشكل (1-2)
وحيث أن القوى المحافظة الوحيدة المؤثرة على الجسم في حالة السقوط هي قوة جذب الأرض للجسم (وزن الجسم)، ولذلك يكون الشغل الناتج عن هذه القوة (Wg) مساوياً إلى:

حيث أن: s = yf - yi ، هي الإزاحة المقطوعة.
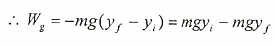
المقدار (mgy) يمثل طاقة الوضع للجسم ويرمز له بالرمز (u) ، وبالتعويض في المعادلة السابقة نحصل على:
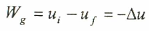
أي أن الشغل يساوي سالب التغير في طاقة وضع الجسم.
وكمثال آخر للقوى المحتفظة ما يتولد من قوة إرجاع (Fs) في النابض عند تعرضه للشد أو الضغط حيث واستناداً لقانون هوك فإن قوة الإرجاع المتولدة تساوي:
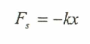
ولذلك فإن الشغل الناتج عنها يساوي:
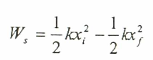
المقدار ( kx½) يمثل طاقة الوضع للنابض ويرمز له بالرمز (us)، وبالتعويض في المعادلة السابقة نحصل على:

أي أن الشغل يساوي التغير في طاقة الوضع.
وحيث أن كلاً من قوة جذب الأرض وقوة إرجاع النابض هي قوى محتفظة (Fc)، إذا يمكن تعميم العلاقة التالية للشغل المحتفظ (Wc):

أن الشغل يمكن أن يعطى بدلالة التغير في الطاقة الحركية للجسم (W = ∆k)، وبالتعويض في المعادلة السابقة نحصل على :
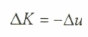
وهذا يعني أن التغير في الطاقة الحركية للجسم سوف يصحبه تغير عكسي بطاقة الوضع للجسم. وبإعادة تنظيم المعادلة نحصل على:

وهذا يعني أن مجموع التغير في الطاقة الحركية وطاقة الوضع سوف يساوي صفراً بالنسبة للقوى المحتفظة. وكما هو معلوم ان مجموع الطاقة الحركية وطاقة الوضع تمثل الطاقة الميكانيكية للجسم (E = K + u)، حيث يمكن كتابة المعادلة السابقة بالشكل التالي:
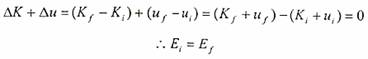
وهذا يعني عدم وجود تغير في الطاقة الميكانيكية للجسم عند تعرضه لقوى محتفظة، وهو ما يسمى بقانون حفظ الطاقة الميكانيكية (Conservation of Mechanical Energy).
1-2- القوى غير المحتفظة:
وهي تلك القوى التي تفقد كلياً أو جزئياً خلال تأثيرها على الأجسام ولا يمكن استرجاع الشغل الناتج عنها بعد انتهاء الحدث، مثل قوة الاحتكاك. وتعتمد قيمة الشغل الناتج من هذه القوى (Wnc) على طبيعة المسار ولا تعتمد على إحداثيات النقطتين اللتان يتحركان بينهما الجسم، وكما يتضح ذلك من الشكل (1-3) حيث يمكن القول أن الشغل المبذول خلال المسار (1) لا يساوي الشغل المبذول خلال المسار (2).

الشكل(1-3)
وحيث أن الشغل الكلي المبذول (Wtot) عند حركة جسم بين نقطتين يساوي مجموع الشغل الناتج من تأثير القوى المحتفظة والقوى غير المحتفظة (قوة الاحتكاك) وكما يلي:
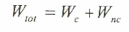
وحيث أن الشغل المبذول يساوي الفرق في الطاقة الحركية للجسم:
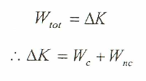
وكما أن : Wc = -∆u
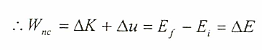
وهذا يعني أن الشغل الناتج من قوى غير محتفظة يساوي الفرق في الطاقة الميكانيكية.



|
|
|
|
لصحة القلب والأمعاء.. 8 أطعمة لا غنى عنها
|
|
|
|
|
|
|
حل سحري لخلايا البيروفسكايت الشمسية.. يرفع كفاءتها إلى 26%
|
|
|
|
|
|
|
جامعة الكفيل تحتفي بذكرى ولادة الإمام محمد الجواد (عليه السلام)
|
|
|