

تاريخ الرياضيات

الاعداد و نظريتها

تاريخ التحليل

تار يخ الجبر

الهندسة و التبلوجي


الرياضيات في الحضارات المختلفة

العربية

اليونانية

البابلية

الصينية

المايا

المصرية

الهندية


الرياضيات المتقطعة

المنطق

اسس الرياضيات

فلسفة الرياضيات

مواضيع عامة في المنطق


الجبر

الجبر الخطي

الجبر المجرد

الجبر البولياني

مواضيع عامة في الجبر

الضبابية

نظرية المجموعات

نظرية الزمر

نظرية الحلقات والحقول

نظرية الاعداد

نظرية الفئات

حساب المتجهات

المتتاليات-المتسلسلات

المصفوفات و نظريتها

المثلثات


الهندسة

الهندسة المستوية

الهندسة غير المستوية

مواضيع عامة في الهندسة

التفاضل و التكامل


المعادلات التفاضلية و التكاملية

معادلات تفاضلية

معادلات تكاملية

مواضيع عامة في المعادلات


التحليل

التحليل العددي

التحليل العقدي

التحليل الدالي

مواضيع عامة في التحليل

التحليل الحقيقي

التبلوجيا

نظرية الالعاب

الاحتمالات و الاحصاء

نظرية التحكم

بحوث العمليات

نظرية الكم

الشفرات

الرياضيات التطبيقية

نظريات ومبرهنات


علماء الرياضيات

500AD

500-1499

1000to1499

1500to1599

1600to1649

1650to1699

1700to1749

1750to1779

1780to1799

1800to1819

1820to1829

1830to1839

1840to1849

1850to1859

1860to1864

1865to1869

1870to1874

1875to1879

1880to1884

1885to1889

1890to1894

1895to1899

1900to1904

1905to1909

1910to1914

1915to1919

1920to1924

1925to1929

1930to1939

1940to the present

علماء الرياضيات

الرياضيات في العلوم الاخرى

بحوث و اطاريح جامعية

هل تعلم

طرائق التدريس

الرياضيات العامة

نظرية البيان
Constructions
المؤلف:
Tony Crilly
المصدر:
50 mathematical ideas you really need to know
الجزء والصفحة:
112-117
21-2-2016
1991
Proving a negative is often difficult, but some of the greatest triumphs in mathematics do just that. This means proving something cannot be done. Squaring the circle is impossible but how can we prove this?
The Ancient Greeks had four great construction problems:
• trisecting the angle (dividing an angle into three equal smaller angles),
• doubling the cube (building a second cube with twice the volume of the first),
• squaring the circle (creating a square with the same area as a particular circle),
• constructing polygons (building regular shapes with equal sides and angles).
To perform these tasks they only used the bare essentials:
• a straight edge for drawing straight lines (and definitely not to measure lengths),
• a pair of compasses for drawing circles.
If you like climbing mountains without ropes, oxygen, mobile phones and other paraphernalia, these problems will undoubtedly appeal. Without modern measuring equipment the mathematical techniques needed to prove these results were sophisticated and the classical construction problems of antiquity were only solved in the 19th century using the techniques of modern analysis and abstract algebra.
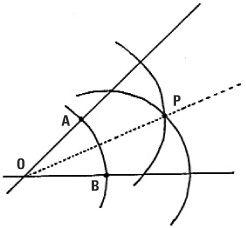
Trisecting the angle
Here is a way to divide an angle into two equal smaller angles or, in other words, bisect it. First place the compass point at O and, with any radius mark off OA and OB. Moving the compass point to A, draw a portion of a circle. Do the same at B. Label the point of intersection of these circles P, and with the straight edge join O to P. The triangles AOP and BOP are identical in shape and therefore the angles AÔP and BÔP will be equal. The line OP is the required bisector, splitting the angle into two equal angles.
Can we use a sequence of actions like this to split an arbitrary angle into three equal angles? This is the angle trisection problem.
If the angle is 90 degrees, a right angle, there is no problem, because the angle of 30 degrees can be constructed. But, if we take the angle of 60 degrees, for instance this angle cannot be trisected. We know the answer is 20 degrees but there is no way of constructing this angle using only a straight edge and compasses. So summarizing:
• you can bisect all angles all the time,
• you can trisect some angles all the time, but
• you cannot trisect some angles at any time.
The duplication of the cube is a similar problem known as the Delian problem. The story goes that the natives of Delos in Greece consulted the oracle in the face of a plague they were suffering. They were told to construct a new altar, twice the volume of the existing one.
Imagine the Delian altar began as a three-dimensional cube with all sides equal in length, say a. So they needed to construct another cube of length b with twice its volume. The volume of each is a3 and b3 and they are related by b3 = 2a3 or b = 3√2 × a where 3√2 is the number multiplied by itself three times that makes 2 (the cube root). If the side of the original cube is a = 1 the natives of Delos had to mark off the length 3√2 on a line. Unfortunately for them, this is impossible with a straight edge and compasses no matter how much ingenuity is brought to bear on the would-be construction.
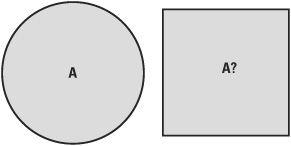
Squaring the circle
Squaring the circle
This problem is a little different and is the most famous of the construction problems:
To construct a square whose area is equal to the area of a given circle.
The phrase ‘squaring the circle’ is commonly used to express the impossible. The algebraic equation x2 – 2 = 0 has specific solutions 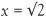 and
and 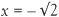 . These are irrational numbers (they cannot be written as fractions), but showing the circle cannot be squared amounts to showing that π cannot be a solution of any algebraic equation. Irrational numbers with this property are called transcendental numbers because they have a ‘higher’ irrationality than their irrational cousins like √2.
. These are irrational numbers (they cannot be written as fractions), but showing the circle cannot be squared amounts to showing that π cannot be a solution of any algebraic equation. Irrational numbers with this property are called transcendental numbers because they have a ‘higher’ irrationality than their irrational cousins like √2.
Mathematicians generally believed that π was a transcendental but this ‘riddle of the ages’was difficult to prove until Ferdinand von Lindemann used a modification of a technique pioneered by Charles Hermite. Hermite had used it to deal with the lesser problem of proving that the base of natural logarithms, e, was transcendental .
Following Lindemann’s result, we might think that the flow of papers from the indomitable band of ‘circle-squarers’ would cease. Not a bit of it. Still dancing on the sidelines of mathematics were those reluctant to accept the logic of the proof and some who had never heard of it.
Constructing polygons
Euclid posed the problem of how to construct a regular polygon. This is a symmetrical many-sided figure like a square or pentagon, in which sides are all of equal length and where adjacent sides make equal angles with each other. In his famous work the Elements (Book 4), Euclid showed how the polygons with 3, 4, 5 and 6 sides could be constructed using only our two basic tools.
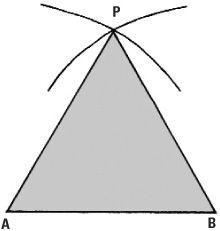
Constructing an equilateral triangle
The polygon with 3 sides is what we normally call an equilateral triangle and is particularly straightforward to construct. However long you want your triangle to be, label one point A and another B with the desired distance in between. Place the compass point at A and draw a portion of the circle of radius AB. Repeat this with the compass point at B using the same radius. The intersection point of these two arcs is at P. As AP = AB and BP = AB all three sides of the triangle APB are equal. The actual triangle is completed by joining AB, AP and BP using the straight edge.
If you think having a straight edge seems rather a luxury, you’re not alone – the Dane Georg Mohr thought so too. The equilateral triangle is constructed by finding the point P and for this only the compasses are required – the straight edge was only used to physically join the points together. Mohr showed that any construction achievable by straight edge and compasses can be achieved with the compasses alone. The Italian Lorenzo Mascheroni proved the same results 125 years later. A novel feature of his 1797 book Geometria del Compasso, dedicated to Napoleon, is that he wrote it in verse.
A prince is born
Carl Friedrich Gauss was so impressed by his result showing a 17-sided polygon could be constructed that he decided to put away his planned study of languages and become a mathematician. The rest is history – and he became known as the ‘prince of mathematicians’. The 17-sided polygon is the shape of the base of his memorial at Göttingen, Germany, and is a fitting tribute to his genius.
For the general problem, the polygons with p sides where p is a prime number are especially important. We have already constructed the 3-sided polygon, and Euclid constructed the 5-sided polygon but he could not construct the 7-sided polygon (the heptagon). Investigating this problem as a 17 year old, a certain Carl Friederich Gauss proved a negative. He deduced that it is not possible to construct a p-sided polygon for p = 7, 11 or 13.
But Gauss also proved a positive, and he concluded that it is possible to construct a 17-sided polygon. Gauss actually went further and proved that a p-sided polygon is constructable if and only if the prime number p is of the form
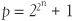
Numbers of this form are called Fermat numbers. If we evaluate them for n = 0, 1, 2, 3 and 4, we find they are the prime numbers p = 3, 5, 17, 257 and 65,537, and these correspond to a constructible polygon with p sides.
When we try n = 5, the Fermat number is p = 232 + 1 = 4,294,967,297. Pierre de Fermat conjectured that they were all prime numbers, but unfortunately this one is not a prime number, because 4,294,967,297 = 641 × 6,700,417. If we put n = 6 or 7 into the formula the results are huge Fermat numbers but, as with 5, neither is prime.
Are there any other Fermat primes? The accepted wisdom is that there are not, but no one knows for sure.
the condensed idea
Take a straight edge and a pair of compasses . . .

 الاكثر قراءة في هل تعلم
الاكثر قراءة في هل تعلم
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















