
تاريخ الفيزياء

علماء الفيزياء


الفيزياء الكلاسيكية

الميكانيك

الديناميكا الحرارية


الكهربائية والمغناطيسية

الكهربائية

المغناطيسية

الكهرومغناطيسية


علم البصريات

تاريخ علم البصريات

الضوء

مواضيع عامة في علم البصريات

الصوت


الفيزياء الحديثة


النظرية النسبية

النظرية النسبية الخاصة

النظرية النسبية العامة

مواضيع عامة في النظرية النسبية

ميكانيكا الكم

الفيزياء الذرية

الفيزياء الجزيئية


الفيزياء النووية

مواضيع عامة في الفيزياء النووية

النشاط الاشعاعي


فيزياء الحالة الصلبة

الموصلات

أشباه الموصلات

العوازل

مواضيع عامة في الفيزياء الصلبة

فيزياء الجوامد


الليزر

أنواع الليزر

بعض تطبيقات الليزر

مواضيع عامة في الليزر


علم الفلك

تاريخ وعلماء علم الفلك

الثقوب السوداء


المجموعة الشمسية

الشمس

كوكب عطارد

كوكب الزهرة

كوكب الأرض

كوكب المريخ

كوكب المشتري

كوكب زحل

كوكب أورانوس

كوكب نبتون

كوكب بلوتو

القمر

كواكب ومواضيع اخرى

مواضيع عامة في علم الفلك

النجوم

البلازما

الألكترونيات

خواص المادة


الطاقة البديلة

الطاقة الشمسية

مواضيع عامة في الطاقة البديلة

المد والجزر

فيزياء الجسيمات


الفيزياء والعلوم الأخرى

الفيزياء الكيميائية

الفيزياء الرياضية

الفيزياء الحيوية

الفيزياء العامة


مواضيع عامة في الفيزياء

تجارب فيزيائية

مصطلحات وتعاريف فيزيائية

وحدات القياس الفيزيائية

طرائف الفيزياء

مواضيع اخرى
ENERGY LEVELS DESCRIBED BY ORBITAL ANGULAR MOMENTUM
المؤلف:
Mark Csele
المصدر:
FUNDAMENTALS OF LIGHT SOURCES AND LASERS
الجزء والصفحة:
p60
9-3-2016
2153
ENERGY LEVELS DESCRIBED BY ORBITAL ANGULAR MOMENTUM
The question begs: Why do electron energies depend on the orbital quantum number anyway? This is, after all, at the root of explaining why the Bohr model fails to explain the spectra of multi electron atoms (like helium, which has two electrons completely filling the 1s orbital). We would expect that all electrons in an n = 2 state have exactly the same energy, regardless of orbital configuration. Some electrons in higher orbitals (e.g., p or d) will have larger angular momentum, others will be closer to the nucleus, but either way, we would expect the same total energy for each electron here. This is not the case, and electrons in various orbital configurations do indeed have different energies. The answer lies in the shielding effect of electron shells. Consider, as illustrated in Figure 1.1, atoms of hydrogen and sodium, each with a single electron in the
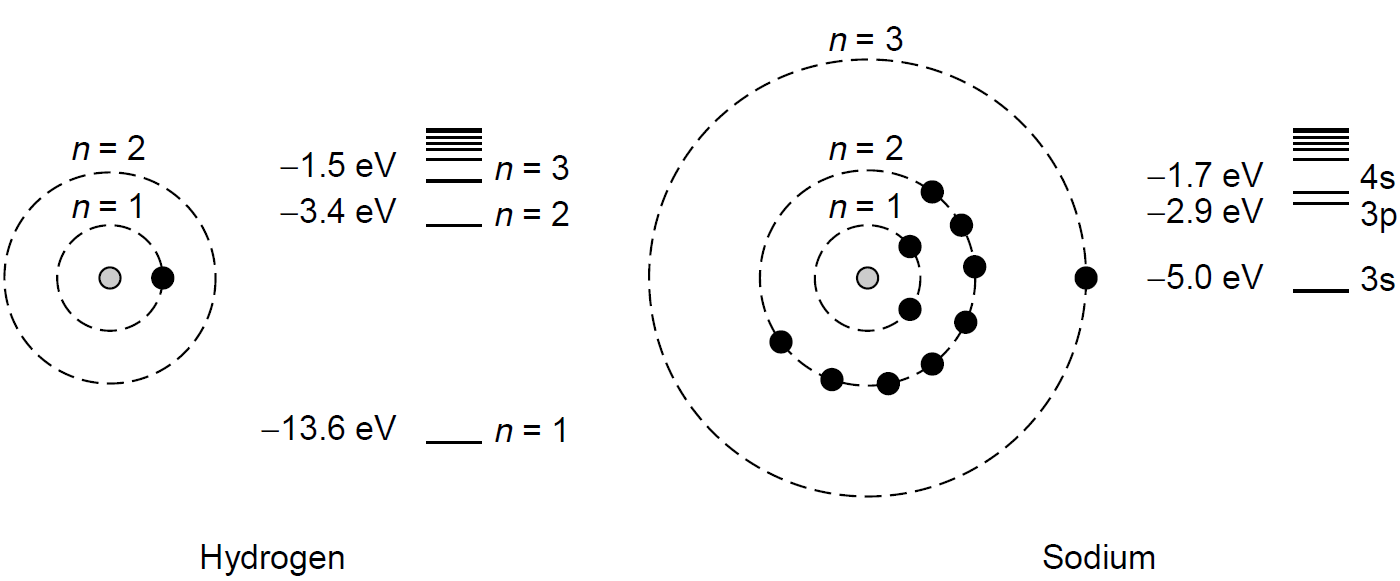
Figure 1.1. Energy shells and levels in hydrogen and sodium.
outer shell. This outer electron is called the valence electron because it lies outside the closed shells below it (e.g., the n = 1 shell of sodium, which is full at two electrons and hence called closed, or the n = 2 shell with eight electrons, which is also full). At face value the energies of electrons in the outer shell of the sodium atom should be calculable by the same methodology as Bohr applied to the hydrogen atom. Spectroscopic studies, however, reveal that electrons in the n = 3 orbit have significantly lower energies than electrons of the hydrogen atom in the same n = 3 orbit. As an example consider the hydrogen atom, with its n = 3 orbit energy of 21.5 eV. The comparable orbit in the sodium atom is the 3s orbit (ground state for sodium), which in this case has an energy of 25.0 eV, which is even lower than hydrogen’s n = 2 orbit energy! The reason for the shift in energy levels is attributed to a shielding effect of the completed inner shells, which serve to lower the energy of the levels outside these. In effect, the inner shells, complete with all electrons, prevent the solitary electron in the outer shell from “feeling” the full attraction of the positive nucleus of the atom. The farther away these outer shell electrons are from the nucleus, the more closely their energies match those of the electron in the hydrogen atom at the same state. It is found that an outer electron of a sodium atom in a 3s state has energy much lower than an electron in a hydrogen atom also in the 3s state. An electron with a higher orbital quantum state, such as l = 2 (in a 3d state), will have an energy almost identical to that of an n = 3 electron in the hydrogen atom at 21.5 eV, as it is farther from the nucleus (using the Bohr analogy of shells). Similarly, 4d and 5d orbitals have energies almost identical to that of hydrogen’s n = 4 and n = 5 state, respectively. Figure 1.2 illustrates the dependence of energy levels on the orbital quantum
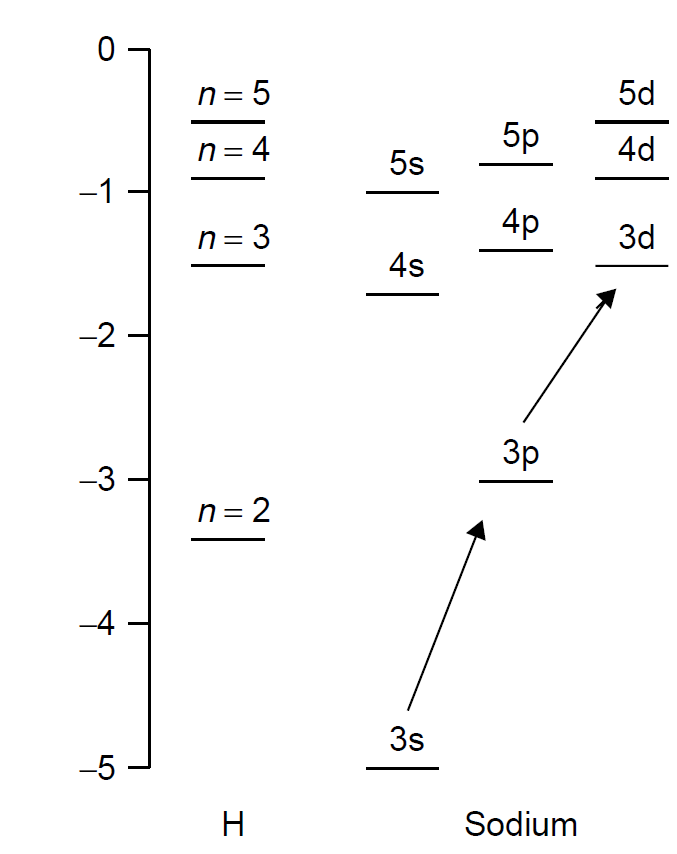
Figure 1.2. Dependence of energy on orbital quantum number.
Consider the outer electron of sodium, normally in the 3s state (third orbit, l = 0). When energy is injected into the atom, that electron may rise to the 3p state next (remember that in the Bohr model this state does not exist and the next state is simply n = 4). As yet higher energies are attained by the electron, it can achieve a 4s state. This state is still below that of the hydrogen’s n =3 state! This model, then, allows for a host of intermediate states between the Bohr states of n = 2 and n = 3 and explains many emission lines which are impossible to explain using the Bohr model. In a multi electron atom (such as helium with two valence electrons) the direction of the angular momentum of each electron will also contribute to splitting of energy levels. If two electrons are orbiting in the same direction, their total angular momentum will be large but they will meet less often than if they were orbiting in the opposite direction. The repulsive force between the electrons is hence lower, and the resulting total energy of that level is lower. This effect is called orbit-orbit interaction.
 الاكثر قراءة في ميكانيكا الكم
الاكثر قراءة في ميكانيكا الكم
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















