


 الفيزياء الكلاسيكية
الفيزياء الكلاسيكية
 الكهربائية والمغناطيسية
الكهربائية والمغناطيسية
 علم البصريات
علم البصريات
 الفيزياء الحديثة
الفيزياء الحديثة
 النظرية النسبية
النظرية النسبية
 الفيزياء النووية
الفيزياء النووية
 فيزياء الحالة الصلبة
فيزياء الحالة الصلبة
 الليزر
الليزر
 علم الفلك
علم الفلك
 المجموعة الشمسية
المجموعة الشمسية
 الطاقة البديلة
الطاقة البديلة
 الفيزياء والعلوم الأخرى
الفيزياء والعلوم الأخرى
 مواضيع عامة في الفيزياء
مواضيع عامة في الفيزياء|
Read More
Date: 28-3-2021
Date: 21-3-2021
Date: 13-5-2017
|
SPECTROSCOPIC NOTATION AND ELECTRON CONFIGURATION
One can use a vector notation (in which each quantum number, including the ones that come later in this chapter, are listed in order) to describe a given quantum state, but the notation commonly used to describe atomic energies was one devised by spectroscopists long before quantum mechanics. Features of the atomic spectra (emission lines) were defined as sharp, principal, diffuse, and fundamental, based on how they appeared when viewed. These descriptions fit those provided by the orbital quantum number, in that sharp lines were found to be associated with the l = 0 state and diffuse lines with the l = 2 state. For any given value of n, then, there are a number of possible states of l, and each value of l is assigned a letter
as follows:
Sharp s l = 0
Principal p l = 1
Diffuse d l = 2
Fundamental f l = 3
g l = 4
h l = 5
For states l = 0 to l = 3 the system uses the letters s, p, d, and f; higher-order states after l = 3 continue with consecutive letters g, h, i, and so on. So what do these numbers l really represent? For given values of n (the principal quantum number from the Bohr model corresponding to radius), one can apply wave mechanics to solve the complex wave functions for electrons and to determine the probability of finding an electron in a particular space. Put a different way, Bohr described electrons in circular orbits where the energy depends solely on distance from the nucleus. In quantum mechanics an electron having a particular energy can be described as having a good probability of being in a certain defined area. In each area, called a probability distribution, the angular momentum (and hence energy) is the same analogous to a noncircular orbit in classical kinematics. These areas of probability can be various shapes and sizes. We begin by solving the radial part of the wave function (i.e., in one axis). Solutions for the first three orbitals 1s, 2s, and 2p are plotted as probabilities in Figure 1.1. The x-axis is in units of Bohr radii and represents the distance of the electron from the nucleus, while the y-axis is the probability of finding the electron at that radius. For the 1s orbital, the probability is high that the electron will be found at a radius of a0 from the nucleus: exactly what Bohr would have predicted for the hydrogen atom’s n = 1 state. This illustrates how quantum mechanics leads us to the same answer as Bohr (at least for a hydrogen like atom) derived, albeit using a completely different approach. For a 2s orbital the probability is highest that the electron will be found at a radius of about 5a0 from the nucleus, but there is also a good probability of finding the electron much closer to the nucleus.
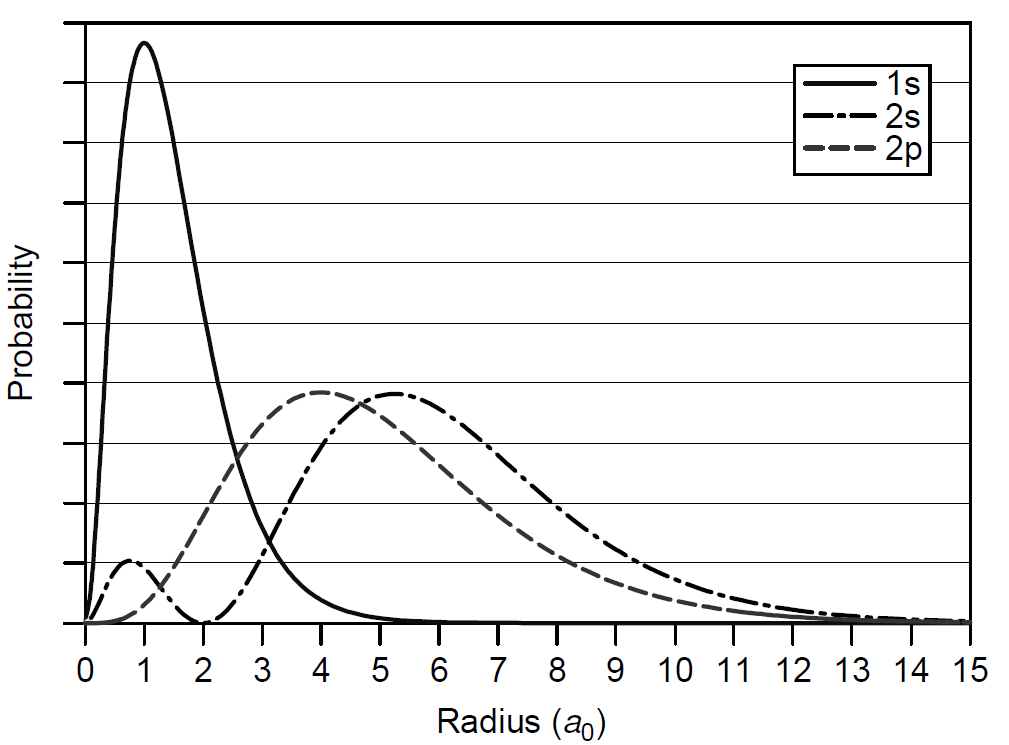
Figure 1.1. Radial probabilities for the first three orbitals of hydrogen.
We must remember that the electron occupies three dimensional space, so although Figure 1.1 shows us the most probable radius from the nucleus in one axis, there is an angular component as well in the solution of the wave functions that shapes these orbitals. Several are depicted in Figure 1.2 as three dimensional figures. Orbitals with zero angular momentum (i.e., l = 0 or s orbitals) have a probability distribution similar to that of a Bohr orbit; the 1s orbital, for example, has the appearance of a sphere around the nucleus. As we move toward electron states with more angular momentum (i.e., p and d orbitals), these probability distributions often take the form of lobes and toruses around the nucleus. For the n = 2 state there are two possibilities for l and hence two possible electron configurations. When l = 0, the orbital resembles two concentric three-dimensional spheres in what is termed the 2s configuration, and when l =1, the orbital does not resemble a circle at all but rather three sets of two lobes, like dumbbells about the center, each in a different axis in what is the 2p configuration. For n = 3, even more orbitals are possible, with three possible states for orbital angular momentum (l = 0, 1, or 2). It is apparent that the term orbit is misleading and why in quantum physics we speak of probability distributions (although the terms shell and orbital are still used by convention as they are in this book). Each value of l represents an electron orbital, and each can hold a maximum number of electrons before it is completely filled. Once filled, additional electrons will begin to fill the next highest orbital based on order of energy. An s orbital can hold a maximum of two electrons, a p orbital a maximum of six electrons, a d orbital a maximum of 10 electrons, and an f orbital a maximum of 14 electrons. Consider the hydrogen atom with a single electron in a 1s orbital at ground state the orbitals are similar to Bohr’s circular orbit. The sodium atom at ground state, however, has a total of 11 electrons. Two electrons will populate the 1s state first, filling this level completely, followed by two more in the 2s state and six electrons in the 2p state, also filling these levels completely. This leaves a single electron in the next outermost orbital, the 3s state. Its electron configuration is described as 1s2 2s2 2p6 3s1, where the superscript after each description for l denotes the number of electrons
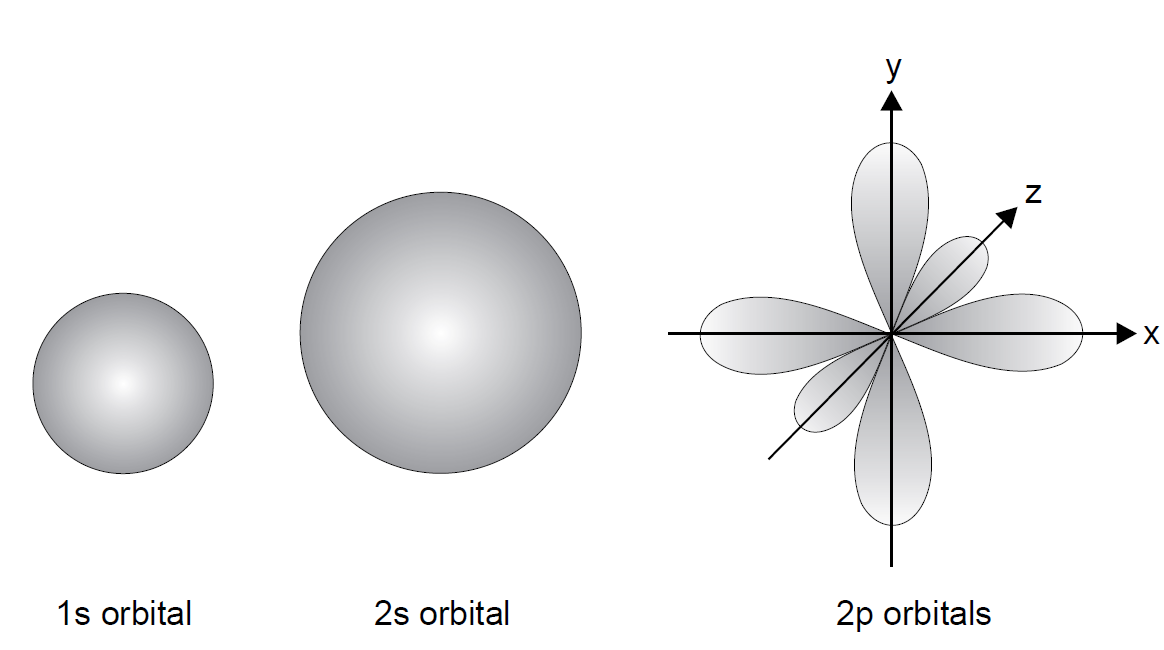
Figure 1.2. Probability distributions for various orbitals.
in that state. Electrons in the outermost, unfilled orbitals are termed valence electrons. When the outer electron in the sodium atom is excited, it can be elevated to a higher state, so the electron configuration might, as an example, be 1s2 2s2 2p6 4p1 or 1s22s22p65d1 for an excited atom. The reasons for the particular way in which orbitals are filled and why, for example, an s orbital can hold only two electrons will be seen later in the chapter, after additional quantum numbers have been introduced. Transitions can occur between any energy state to yield photon emission, and unlike the Bohr model, where electrons could be in only one principal quantum state (n = 2, n = 3, etc.), many more levels are now available. With angular momentum now in the picture, each level of n will now have n possible values of l. If the outer electron of the sodium atom is elevated in energy from its lowest or ground state energy (n = 3) to an n =5 level, there are five possible energies that it can assume there (with l ranging from 0 to 4), so a large number of transitions are possible.



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|