WAVE  PROPERTIES  OF  PARTICLES  (DUALITY)

Although classical physicists had thought of electromagnetic radiation as a wave for many years, experimental evidence provided by the photoelectric effect had shown that depending on the circumstances, it could exhibit particle qualities. The converse is also true: A particle can exhibit wave behavior. In 1924, Louis deBroglie attempted to calculate the wavelength associated with a particle. By combining the Planck Einstein relation for photons, E = hv (stating that the energy of the photon was related to the frequency or wavelength), with Einstein’s famous statement of mass to energy equivalency, E = mc², he speculated that wave behavior was a property of all moving objects and developed a mathematical relationship allowing determination of wavelength. At face value this seems absurd, but under the right circumstances wave behavior is indeed observed, as we shall see in the next section, where an electron, clearly a particle, exhibits wave behavior under the right circumstances. Central to deBroglie’s hypothesis was that any particle with momentum has an associated wavelength. This relation is easily derived from the Einstein Planck equation combined with the relation for an electromagnetic wave, namely E = cp, where c is the speed of light and p is the momentum, as follows:

E = hv = cp   yielding   hv = cp   (1.1)

Substituting for n = c/λ, we now get λ = h/p. Relation (1.1) holds true for low energy particles, where the momentum can be found using a simple relation from kinematics: namely,

p = (2mE_k)1/2     (1.2)

where E_k is the kinetic energy of the particle and m is the mass. Because of relativity, a glitch occurs when considering high-energy particles. As a particle acquires more energy, it approaches the speed of light. As this happens, the apparent mass of these particles changes and must be accounted for. Factoring in relativity, the deBroglie wavelength for a high-energy particle is simply

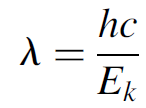 (1.3)

where E_k is the kinetic energy of the particle. The greater the mass and velocity of a particle, the shorter its wavelength. For ordinary macroscopic particles, the wavelength is so short that it can never be measured, but for small subatomic particles with little mass, the wavelengths are well within observable ranges.

Example 1.1 Wavelength Measurement Consider the wavelength of an electron with energy 0.001 eV (or 1.602 ×10^-22 J):

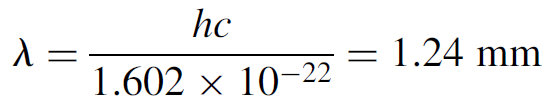
This is in the microwave region of the electromagnetic spectrum and is easily measured. Now consider the wavelength of an electron with energy 2.0 eV (or 3.204 × 10^-19 J). The wavelength is found to be 620 nm, which is in the visible spectrum (red) and is easily measured using a spectroscope. Similarly, an electron with energy 10 keV has a wavelength of 1.24 × 10^-10 m. This is in the x-ray region of the electromagnetic spectrum. With wavelengths this short it is not possible to use a diffraction grating (as we use for visible light) since the spacing between the lines needs be so close that such a grating cannot be manufactured. A simple solution is to use a crystal as a diffraction grating. The spacing of atoms in the crystal is just right to allow diffraction to occur when x-rays are beamed at the crystal. In this manner an x-ray spectrometer can be built which works in the same manner as an optical spectroscope, where by measuring the angle of diffraction, the wavelength of the incident radiation may be determined. Finally, consider a macroscopic object such as a 150-g ball hurled at 20 m/s. The kinetic energy of the ball is

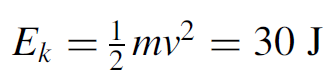
so the wavelength is

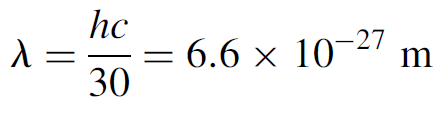
This wavelength is far too short to measure it is well beyond cosmic rays (the shortest wavelength radiation known). This illustrates why normal everyday (i.e., macroscopic) objects do not exhibit wave behavior (or at least observable wave behavior).