


 النبات
النبات
 الحيوان
الحيوان
 الأحياء المجهرية
الأحياء المجهرية
 علم الأمراض
علم الأمراض
 التقانة الإحيائية
التقانة الإحيائية
 التقنية الحيوية المكروبية
التقنية الحيوية المكروبية
 التقنية الحياتية النانوية
التقنية الحياتية النانوية
 علم الأجنة
علم الأجنة
 الأحياء الجزيئي
الأحياء الجزيئي
 علم وظائف الأعضاء
علم وظائف الأعضاء
 الغدد
الغدد
 المضادات الحيوية
المضادات الحيوية|
Read More
Date: 13-4-2016
Date: 20-4-2016
Date: 20-4-2016
|
Non-linear electrophoresis
Electrophoresis can be visualized by an analogy. Imagine spherical glass marbles rolling down a slope in a tank of syrup. The profile of the slope could be described by plotting contour lines. The marbles would move very slowly because of the viscosity of the syrup and so they would essentially acquire no momentum. As a result they would always move in the direction of the slope, even if this was to change its direction, i.e. the locus of any one marble would always be at right angles to the contour lines. The locus would reflect the direction of the force vector acting upon each marble and the magnitude of the force would be inversely proportional to the spacing between the contour lines. In electrophoresis, the equivalent of contour lines would be is voltage contours and the loci of ions undergoing electrophoresis would correspond to field lines, which are always at right angles to the is voltage contour lines.
In most forms of electrophoresis, the field lines are straight and the is voltage contours are evenly spaced. In the marbles-in-syrup analogy, this is equivalent to the marbles moving down a straight plane surface, inclined at an angle to the horizontal. However, deviating from this straight and narrow approach can be instructive and one can pose a number of “what if?” questions to probe one's own insight into electrophoresis, e.g.
What if the gel was of increasing cross-section, i.e. either conical or wedge-shaped?
What if the gel was not straight, but went through a 90 bend?
What if the gel had a hole cut in it (say if there was a pillar passing through the gel)?
These questions have been explored theoretically and empirically by Dennison . If the gel were conical or wedge-shaped, the voltage gradient (dV/dx) would be steeper at the narrow end and shallower at the wider end. The net result is that the migration of slower ions would be increased, as they would spend more time in the steep part of the gradient, whereas that of faster ions would be slowed as they would reach the shallower parts the gradient more quickly. Normally, in gel electrophoresis the mobility of ions is a logarithmic function of their molecular weight, so that small ions are separated better than larger ions. In a wedge-shaped gel the relationship is made more linear. Although this result has not found much utility in the separation of proteins, wedge gels have proved useful in the separation of nucleic acids. In DNA sequencing gels, a greater number of bases can be sequenced in a wedge gel compared to a straight-sided slab gel, and the separation of plasmids is also improved in wedge-shaped gels. The wedge-gel concept has been extended to preparative electrophoresis by Rolchigo and Graves, and to IEF by An empirical analysis of electrophoresis around corners was done by Dennison (Fig. 1). Around a comer, the is voltage contours remain as straight lines but become closer together on the inside of the corner than on the outside, rather like the steps in a spiral staircase. As a result, the voltage gradient is steeper on the inside of the corner and the proteins on this side will accelerate when negotiating the corner. By contrast, the isovoltage contours are further apart on the outside of the corner and the proteins will slow down. The net result is that the protein band will become skewed as it rounds the comer. Negotiating a second comer in the opposite direction does not undo the distortion.
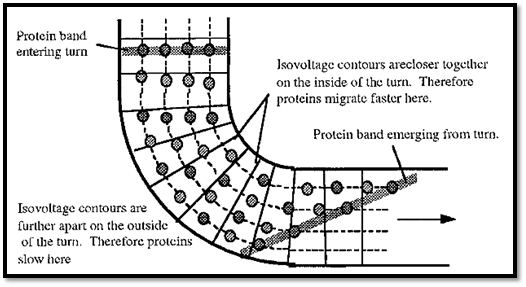
Figure 1. The effect of a bend in the gel upon electrophoretic behaviour in PAGE.
Electrophoresis around a circular obstruction in the gel is shown in Fig. 2. The isovoltage contour lines (shown as solid lines) can easily be visualized, remembering the fact that they are always at right angles to the field lines (shown as dotted lines). An interesting conclusion was drawn from these experiments, i.e. that the equations describing the behaviour of ions undergoing electrophoresis are identical to those describing the irrotational flow of an ideal incompressible fluid. Ideal fluid behaviour was previously considered to be only an abstract concept; in an ideal fluid the molecules have no momentum.
If one has a playful nature, the shapes of the voltage gradient surfaces can be visualized on a visit to the beach. Pouring loose beach-sand down a slope, in which a circular obstruction has been placed, will form a contoured surface around the obstruction. In ones minds eye one could imagine this surface in the tank of syrup and visualize the movement of marbles down the surface it will be found to be identical to the behaviour of ions around the circular obstruction shown in Fig. 2! To summarize, the following points can be noted about non-linear electrophoresis:
• Field lines pass smoothly around comers or obstructions and resemble
“streamlines”.
• Ions will migrate along field lines, i.e. the field lines will represent the loci of migrating ions.
• Isovoltage contour lines are always at right angles to the field lines.
• Ions will migrate quickly where the isovoltage contour lines are close
together (i.e. where the voltage gradient is steep) and slowly where the isovoltage contour lines are far apart (i.e. where the voltage gradient is shallow).
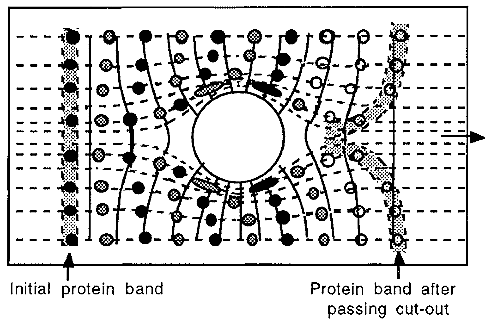
Figure 2. The effect of a circular hole in an electrophoresis gel.
References
Dennison, C. (2002). A guide to protein isolation . School of Molecular mid Cellular Biosciences, University of Natal . Kluwer Academic Publishers new york, Boston, Dordrecht, London, Moscow .
Dennison, C., Lindner, W. A. and Phillips, N. C. K. (1982) Nonuniform field gel electrophoresis. Anal. Biochem. 120, 12-1 8 (1 982).
Dennison, C., Phillips, A. M. and Nevin, J. M. (1983) Nonlinear gel electrophoresis: an analogy with ideal fluid flow. Anal. Biochem. 135, 379-382.
Ansorge, W. and Labiet, S. (1 984) Field gradients improve resolution on DNA sequencing gels. J. Biochem. Biophys. Methods 10, 237-243.
Bonicelli, E., Simeone, A., deFalco, A., Fidanza, V. and La Volpe, A. (1983) An agarose gel resolving a wide range of DNA fragment lengths. Anal. Biochem. 134, 40-43.
Olsson, A., Moks, T., Uhlen, M. and Gaal, A. B. (1984) Uniformly spaced banding pattern in DNA sequencing gels by use of field-strength gradient. J. Biochem. Biophys. Methods 10, 83-90.
Rochelle, P. A., Day, M. J. and Fry, J. C. (1986) The use of agarose wedge-gel electrophoresis for resolving both small and large naturally occurring plasmids. Lett. Appl. Micro. 2, 47-51.



|
|
|
|
دراسة: حفنة من الجوز يوميا تحميك من سرطان القولون
|
|
|
|
|
|
|
تنشيط أول مفاعل ملح منصهر يستعمل الثوريوم في العالم.. سباق "الأرنب والسلحفاة"
|
|
|
|
|
|
|
الطلبة المشاركون: مسابقة فنِّ الخطابة تمثل فرصة للتنافس الإبداعي وتنمية المهارات
|
|
|