


 الفيزياء الكلاسيكية
الفيزياء الكلاسيكية
 الكهربائية والمغناطيسية
الكهربائية والمغناطيسية
 علم البصريات
علم البصريات
 الفيزياء الحديثة
الفيزياء الحديثة
 النظرية النسبية
النظرية النسبية
 الفيزياء النووية
الفيزياء النووية
 فيزياء الحالة الصلبة
فيزياء الحالة الصلبة
 الليزر
الليزر
 علم الفلك
علم الفلك
 المجموعة الشمسية
المجموعة الشمسية
 الطاقة البديلة
الطاقة البديلة
 الفيزياء والعلوم الأخرى
الفيزياء والعلوم الأخرى
 مواضيع عامة في الفيزياء
مواضيع عامة في الفيزياء|
أقرأ أيضاً
التاريخ: 27-4-2016
التاريخ: 2023-02-11
التاريخ: 21-4-2016
التاريخ: 2023-07-02
|
النسبية والتفاعلات الكهرومغناطيسية
لقد اصبح معروفا الان من ان قانون كولوم هو الاساس في حساب القوة الكهربائية المؤثرة على الشحنات الساكنة. ولكن اذا تحركت تلك الشحنات فان قوة جديدة تظهر لتضاف الى قوة كولوم هي القوة المغناطيسية وقد تم توضيح ذلك سابقا. افتراض اينشتاين في عام 1905 مستعينا بنظريته النسبية ان هاتين القوتين الكهربائية والمغناطيسية تنشآن من القوة الكهربائية. وقد أجريت تجارب كثيرة تتعلق بهذه الدراسة وثبت ان العالم اينشتاين كان على صواب عندما وضع هذا الافتراض. ان هاتين القوتين تم تسميتهما معا بالقوة الكهرومغناطيسية للترابط الوثيق فيما بينهما وان ظهور قوة مغناطيسية يعطي تصحيحا نسبيا لقانون كولوم.
ان جميع الظواهر المغناطيسية التي تحدث هي نتيجة قوى التبادل بين الشحنات الكهربائية المتحركة. فأية شحنة منفردة اذا كانت في حالة حركة تولد حولها مجالا مغناطيسيا. ان هذا المجال يؤثر بقوة مغناطيسية على اية شحنة كهربائية اخرى متحركة فيه يضاف اليها القوة الكهربائية الساكنة (القوة الكهروستاتيكية) التي تظهر بين الشحنتين سواء كانتا في حالة حركة ام ساكنتين.
لم نتطرق لحد هذه اللحظة الى التيارات الكهربائية التي تحملها اسلاك موصلة وكانت معظم دراستنا السابقة مقتصرة على الشحنات الكهربائية المنفردة. اما الان فأننا سنوضح في هذا البند كيفية استنتاج القوة المغناطيسية من قانون كولوم وتأثيرات لورنس في النظرية النسبية.
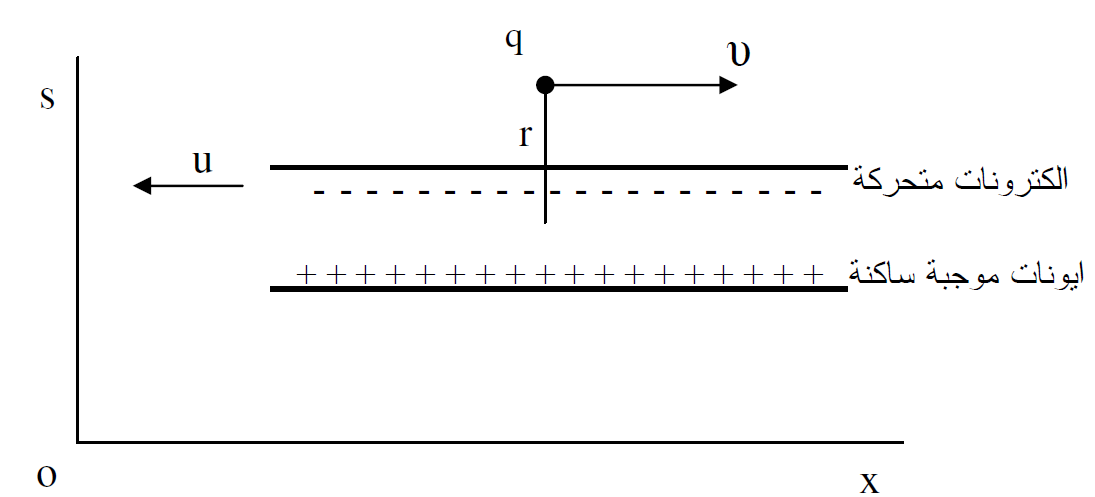
الشكل (1.1) : سلك موصل يحوي الكترونات متحركة وايونات موجبة ساكنة في s.q شحنة نقطية متحركة. محل القوة الكهربائية عليها يساوي صفرًا.
طبقا لقانون كولوم وكما موضح في الشكل (1.1) فان معدل القوة الكهربائية المؤثرة على شحنة q تتحرك بسرعة v بالقرب من موصل يحمل تيارا كهربائيا في محور الاسناد s يساوي صفرًا. لأن الشحنتين الخطيتين الموجبة والسالبة يزيل تأثير أحداهما الأخرى. وبموجب النظرية النسبية الخاصة فان معدل المسافة بين الكترونات التوصل التي تتحرك بسرعة انجراف تساوي v ستقل بواسطة تقلص لورنس بمقدار (1-u2/c2)+1/2 اذن كثافة الشحنة الخطية -λ للإلكترونات المتحركة في هذا المحور ستزداد بمقدار (1-u2/c2)-1/2 فيما تبقى كثافة الشحنة الخطية +λ للأيونات الموجبة دون تغير اي ان 0λ +=λ حيث ان 0λ كثافة الشحنة الخطية للأيونات الموجبة في حالة السكون.
لكي نصل الى النتيجة ننقل الحدث الان الى محور الاسناد sʹ الذي يتحرك بسرعة v بالاتجاه الموجب للإحداثي x كما موضح في الشكل (1.1). ان المشاهد في هذا المحور يلاحظ ان q في حالة سكون وعلى بعد r من موقع السلك وان الالكترونات تتحرك بسرعة uʹ. اما الايونات الموجبة فتشاهد في حالة حركة بسرعة v بالاتجاه السالب للإحداثي x.
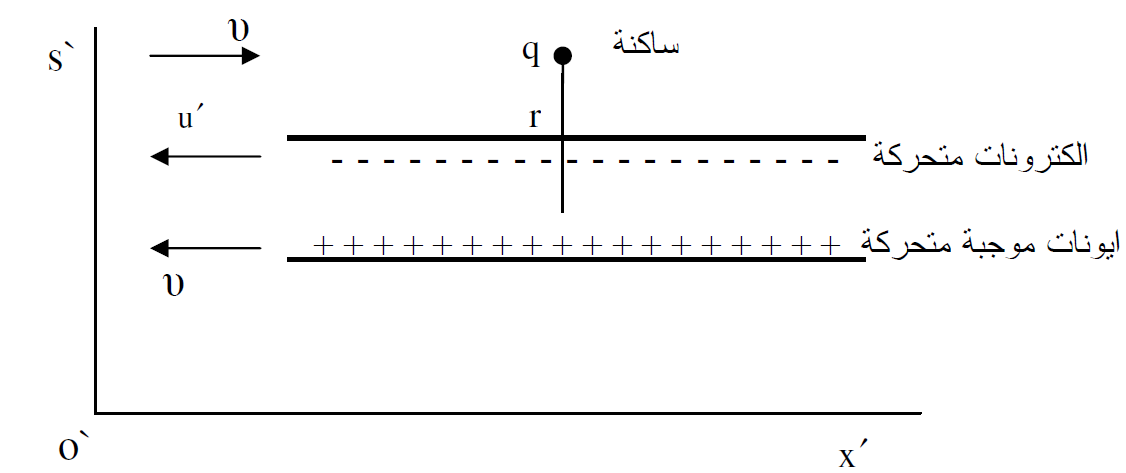
الشكل (1.2) : في محور الاسناد sʹ يلاحظ ان الالكترونات لا تزال في حالة حركة واصبحت الايونات الموجبة تتحرك بالاتجاه السالب للإحداثي x. اما الشحنة q فهي في حالة سكون.
تكتب كثافة الشحنات السالبة والموجبة في هذا المحور كالآتي :
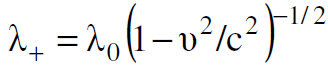 (1.1)
(1.1)
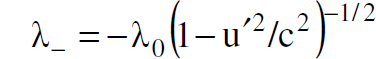 (1.2)
(1.2)
ومن تحويلات السرعة من s الى sʹ فان :

وبفرض ان 1 >>u/c يحصل :
 (1.3)
(1.3)
وبتعويض قيمة uʹ من المعادلة (1.3) في المعادلة (1.2) ينتج :
 (1.4)
(1.4)
واذا فرضنا ان λ الشحنة الكلية الخطية في السلك فان :
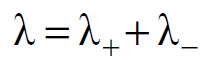 (1.5)
(1.5)
ومن قانون كاوس نجد أن شدة المجال الكهربائي E عند موقع الشحنة q تساوي:
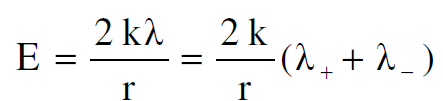
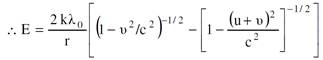 (1.6)
(1.6)
وبما ان 1 >>v/c يكون :
 (1.7)
(1.7)
وبتعويض الطرف الايمن من المعادلة (1.7) في المعادلة (1.6) نحصل على :
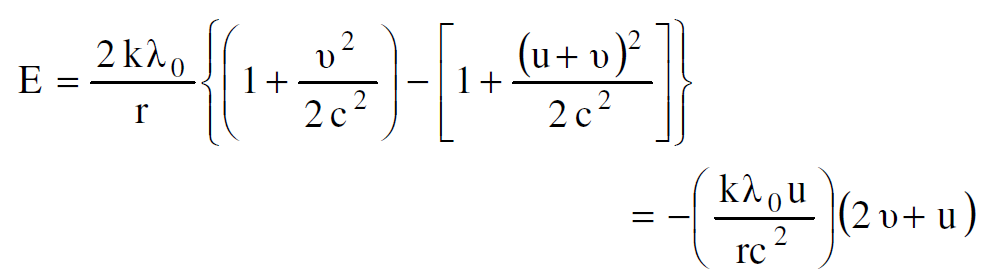
ولأن >> u vيكون :
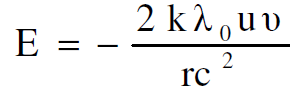 (1.8)
(1.8)
إذن القوة المؤثرة على الشحنة q تساوي :
 (1.9)
(1.9)
حيث ان uλ0 I = ويساوي التيار المار في السلك. اما الاشارة السالبة في المعادلة (1.9) فتشير الى ان القوة هي قوة تجاذب وتمثل القوة المغناطيسية بين شحنة متحركة وسلك يحمل تيارا كهربائيا. وبمقارنة المعادلة (1.9) مع المعادلة  نستنتج ان كثافة الفيض المغناطيسي B تساوي :
نستنتج ان كثافة الفيض المغناطيسي B تساوي :
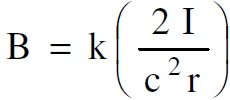 (1.10)
(1.10)
نستنتج مما تقدم انه بسبب عدم تساوي تقلص لورنس للشحنات الخطية الموجبة والسالبة فان السلك الذي يحمل تيارات كهربائيا يكون متعادل الشحنة في محور اسناد معين ولكنه يكون مشحونا في محور اسناد آخر. نستنتج ايضا ان الشحنة q تنجذب نحو السلك بقوة كهربائية خالصة في sʹ حيث يكون السلك مشحونا وتكون الشحنة q في حالة سكون إلا أن القوة تلك لم تعد قوة كهربائية في s حيث يكون السلك متعادل الشحنة. وإذا اخذنا بالاعتبار القوة الكهربائية الساكنة (الكهروستاتيكية) مع النسبية فإننا نضمن وجود قوة اخرى هي القوة المغناطيسية. ومن الممكن ان نكتب المعادلة (1.9) بصيغة اخرى لتكون مألوفة لدينا أكثر إذا عوضنا عن c2 وعن k بما يساويهما اي نكتب 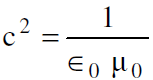 و
و 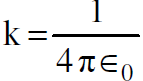 فتتحول العلاقة (1.9) إلى :
فتتحول العلاقة (1.9) إلى :
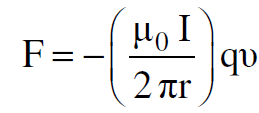 (1.11)
(1.11)
المقدار بين القوسين في المعادلة الأخيرة يمثل كثافة الفيض المغناطيسي لسلك موصل مستقيم وطويل وان القوة F هي تلك التي نحصل عليها من قوة لورنس في محور الاسناد s [لاحظ المعادلة (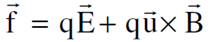 )].
)].
اصبح الان بإمكاننا ان نحسب القوة المغناطيسية بين سلكين طويلين متوازيين المسافة بينهما r ويحمل الاول تيارا مقداره I ويحمل الثاني تيارا مقداره ʹI كما في الشكل (1.3). بما ان كثافة الشحنات السالبة والموجبة متساوية لهذين السلكين فانهما لا يولدان مجالا كهربائيا ولكن كلا منهما يولد مجالا مغناطيسيا يؤثر على الاخر لوجود الكترونات حرة تتحرك داخل السلكين.
نبدأ بحساب القوة بالاستعانة بالعلاقة (1.11) التي تكتب بالصيغة :
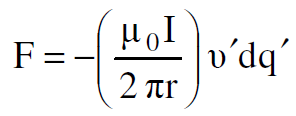 (1.12)
(1.12)
اذ ان dqʹ الشحنة الموجبة المتحركة بسرعة vʹ باتجاه الاحداثي x وعلى بعد r عن موقع السلك الاول الذي يمر فيه تيار يساوي I.
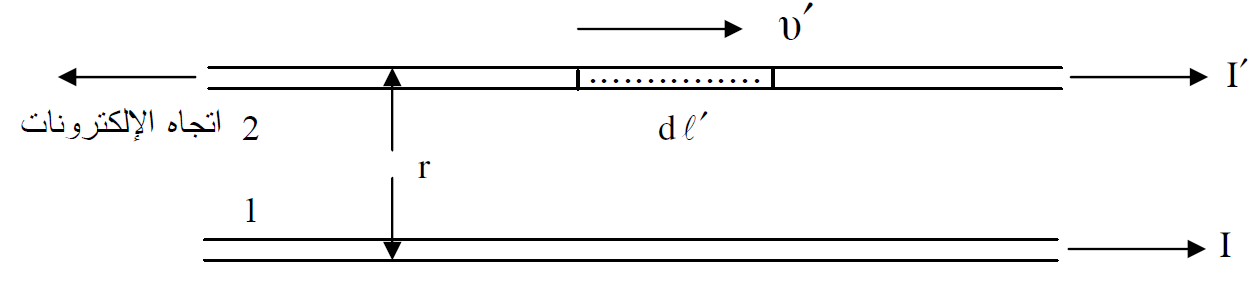
الشكل (1.3) : سلكان موصلان متوازيان احدهما يحمل تيارا لا يساوي التيار الذي يحمله الاخر، الا ان التيارين باتجاه واحد.
اذا اعتبرنا هذه الشحنة تتحرك داخل السلك الثاني مولدة تيارًا كهربائيًا مقداره Iʹ بالاتجاه الموضح في الشكل فان :
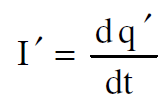
الان Iʹdℓʹ هو عنصر التيار مأخوذ من السلك الثاني ويساوي :
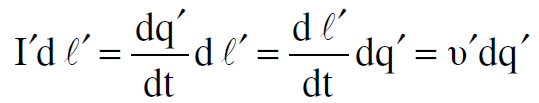
وبتعويض Iʹdℓʹ بدلاً من vʹ dqʹ تتحول العلاقة (1.12) الى الصيغة :
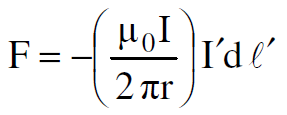 (1.13)
(1.13)
إذن القوة المؤثرة على السلك الثاني لوحدة الطول بسبب المجال المغناطيسي المتولد من السلك الاول تساوي :
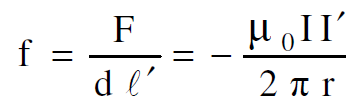 (1.14)
(1.14)
وهذه القوة تؤثر في مستوى السلكين وانها قوة تجاذب وذلك لان التيارين I و Iʹ هما باتجاه واحد. وتتحول هذه القوة الى قوة تنافر اذا انعكس احد التيارين في اي من السلكين. وبصورة عامة اذا مر تيار I في سلك قصير طوله ℓ يقع بالقرب من السلك طويل يحمل تيارا حوله مجالاً مغناطيسياً كثافة فيضه 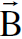 عند موقع السلك القصير في قوة التجاذب او التنافر
عند موقع السلك القصير في قوة التجاذب او التنافر 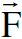 بين السلكين يمكن كتابتها بالصيغة المتجهية الاتية :
بين السلكين يمكن كتابتها بالصيغة المتجهية الاتية :
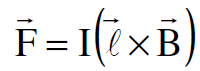 (1.15)
(1.15)
وتجدر الاشارة الى ان التيار I ليس متجها رغم اننا حددنا له اتجاها ليدل على حركة الشحنات الموجبة وهو مصطلح يستخدم لاتجاه التيار وقد طبق في كثير من الكتب الحديثة. اما 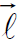 فهو متجه باتجاه حركة الشحنات الموجبة. يتم تحديد اتجاه القوة
فهو متجه باتجاه حركة الشحنات الموجبة. يتم تحديد اتجاه القوة 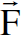 بواسطة قاعدة اليد اليمنى اذ ان الابهام يشير الى اتجاه القوة
بواسطة قاعدة اليد اليمنى اذ ان الابهام يشير الى اتجاه القوة 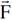 عندما تلف بقية اصابع اليد من المتجه
عندما تلف بقية اصابع اليد من المتجه 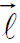 الى المتجه
الى المتجه 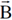 وتقع
وتقع 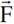 في مستوى السلكين المتوازيين.
في مستوى السلكين المتوازيين.



|
|
|
|
لصحة القلب والأمعاء.. 8 أطعمة لا غنى عنها
|
|
|
|
|
|
|
حل سحري لخلايا البيروفسكايت الشمسية.. يرفع كفاءتها إلى 26%
|
|
|
|
|
|
|
جامعة الكفيل تحتفي بذكرى ولادة الإمام محمد الجواد (عليه السلام)
|
|
|