


 الفيزياء الكلاسيكية
الفيزياء الكلاسيكية
 الكهربائية والمغناطيسية
الكهربائية والمغناطيسية
 علم البصريات
علم البصريات
 الفيزياء الحديثة
الفيزياء الحديثة
 النظرية النسبية
النظرية النسبية
 الفيزياء النووية
الفيزياء النووية
 فيزياء الحالة الصلبة
فيزياء الحالة الصلبة
 الليزر
الليزر
 علم الفلك
علم الفلك
 المجموعة الشمسية
المجموعة الشمسية
 الطاقة البديلة
الطاقة البديلة
 الفيزياء والعلوم الأخرى
الفيزياء والعلوم الأخرى
 مواضيع عامة في الفيزياء
مواضيع عامة في الفيزياء|
أقرأ أيضاً
التاريخ: 24-4-2016
التاريخ: 19-11-2020
التاريخ: 27-4-2016
التاريخ: 24-7-2016
|
انحلال الجسيمات
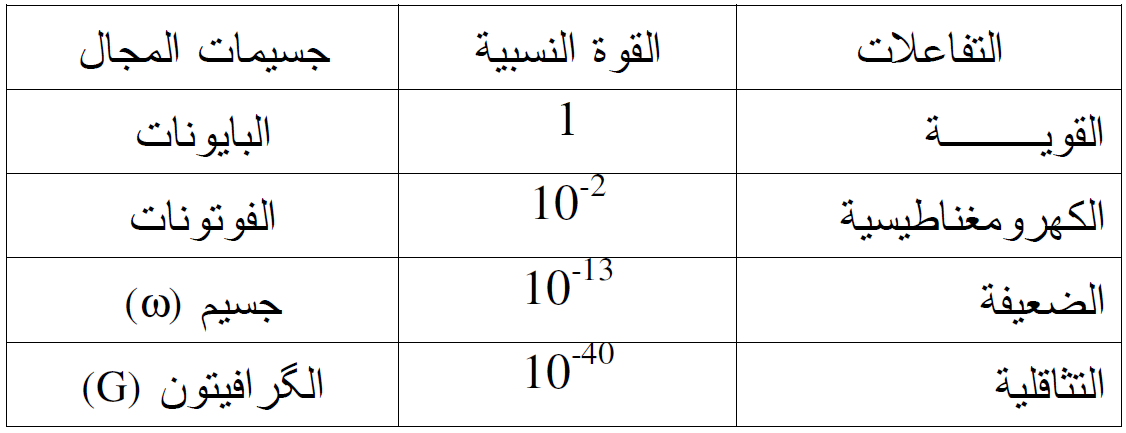
من المعروف ان الجسيمات الاولية تخضع لقوانين فيزياء الطاقة العالية. ولكي نفهم خواص هذه الجسيمات ينبغي علينا ان نكون قادرين على وصف قوى التفاعلات التي تحصل فيما بينها. اذن لابد من التقاء الضوء على هذه التفاعلات وهي : التفاعلات الكهرومغناطيسية التي يتم خلالها تبادل الفوتونات (كمات المجال الكهرومغناطيسية) والتفاعلات النووية حيث يتم تبادل البايونات (π) والكايونات K)) والتفاعلات التثاقلية التي هي اضعف التفاعلات يتم خلالها تبادل الكرافيتونات (G) (كمات المجال التثاقلي) وقد تم افتراضها لهذا النوع من التفاعلات. هذه التفاعلات تحدث بين الاجسام ذات الكتل الكبيرة (كالنجوم مثلا) عند تعرضها لتعجيلات كبيرة جدا.
اما التفاعلات الضعيفة والتي تحدث بين بعض انواع الجسيمات الاولية فيتم تبادل الجسيمات (W) خلالها. وان هذه الجسيمات هي كمات تم افتراضها لهذا النوع من التفاعلات والجدول (1.1) يوضح ذلك.
الجدول (1.1) التفاعلات الاساسية.
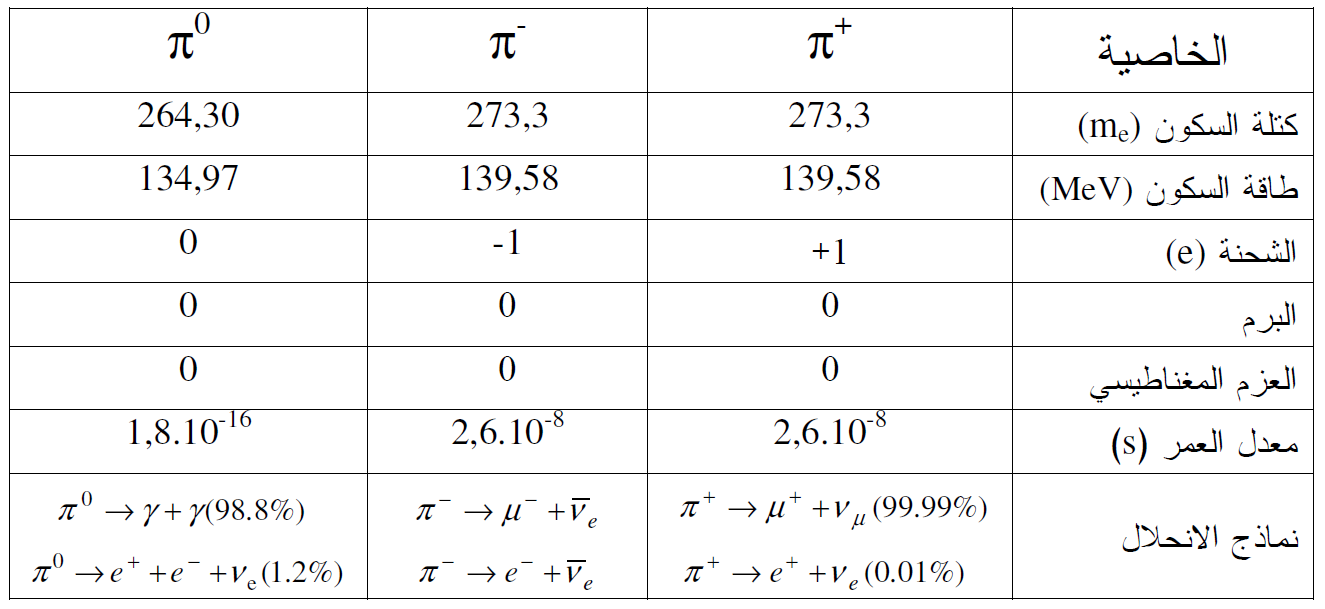
ان جسيمات الاولية، الالكترون e-)) والبروتون (p) والفوتون (γ) والجسيمات الضد، والبوزيترون e+)) وبروتون الضد )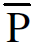 ( لها خصائص جوهرية كالشحنة الكهربائية المحددة وكتلة السكون (أو طاقة السكون) و الزخم الزاوي والبرم ومعدل العمر قبل الانحلال حيث ان هذه الجسيمات الخمسة هي جسيمات مستقرة ضد الانحلال التلقائي ولها معدل عمر لانهائي كما موضح في الجدول (1.2).
( لها خصائص جوهرية كالشحنة الكهربائية المحددة وكتلة السكون (أو طاقة السكون) و الزخم الزاوي والبرم ومعدل العمر قبل الانحلال حيث ان هذه الجسيمات الخمسة هي جسيمات مستقرة ضد الانحلال التلقائي ولها معدل عمر لانهائي كما موضح في الجدول (1.2).
الجدول (1.2) : بعض الخصائص لبعض الجسيمات الاولية.
سنكتفي بتوضيح كيفية تبادل الفوتونات خلال التفاعلات الكهرومغناطيسية، والبايونات خلال التفاعلات القوية (النووية) حيث سنأخذ التفاعل بين الكترونين كمثال على التفاعلات الكهرومغناطيسية لتوضيح كيفية تبادل الفوتونات بينهما. ففي الشكل (1.1) نلاحظ ان الالكترون في النقطة A يبعث فوتونا وهمية بطاقة تساوي γε وبزخم خطي pγ فيرتد الالكترون الى اليسار بسرعة تساوي (u << c) u وبعد فترة معينة من الزمن يتم امتصاص هذا الفوتون من قبل الالكترون الموجود في النقطة B الذي يرتد بعدها الى اليمين بالسرعة نفسها u، بافتراض ان الزخم الخطي محفوظ دائما قبل وخلال وبعد تبادل الفوتونات. ولتوضيح ذلك لابد من حساب الطاقة (Δεγ) المتبادلة بين الالكترونين خلال فترة زمنية Δt)).
قبل انبعاث الفوتون الوهمي من الالكترون الموجود في النقطة A تكون طاقة النظام هي عبارة عن طاقة السكون الكلية )0ε) للإلكترون. وبافتراض ان الزخم الخطي الكلي يساوي صفرا فان انبعاث الفوتون سوف يمنح زخما الي الالكترون مقداره Pe)) اي أن :
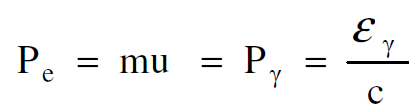 (1.1)
(1.1)
حيث أن m كتلة الالكترون و u سرعته.
وبتطبيق قانون حفظ الطاقة من الممكن حساب الطاقة الكلية ε بعد الانبعاث وقبل حدوث عملية الامتصاص وهي :
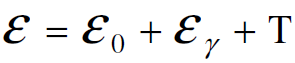 (1.2)
(1.2)
حيث ان T الطاقة الحركية للإلكترون وتساوي 1/2mu2في حال اهمال التأثيرات النسبية.
اذن الطاقة المتبادلة بين الالكترونين تساوي :
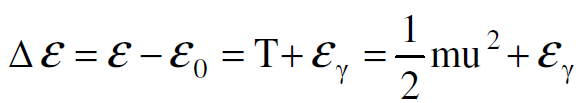 (1.3)
(1.3)
ومن العلاقة (1.1) نجد أن :
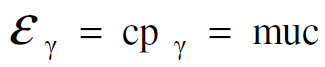 (1.4)
(1.4)
وبتعويض المعادلة (1.4) في المعادلة (1.3) نحصل على :
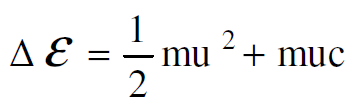 (1.5)
(1.5)
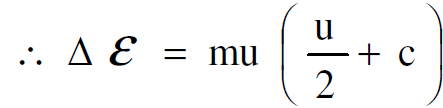 (1.6)
(1.6)
وبما ان u<<c تختزل المعادلة الاخيرة الى :
 (1.7)
(1.7)
نستنتج من المعادلة (1.7) ان الطاقة المتبادلة هي طاقة الفوتون الوهمي خلال فترو زمنية مساوية الى (Δt) و بواسطة مبدأ اللايقين لهايزنبرك بصيغته الثانية من الممكن حساب هذه الفترة الزمنية التي تم بواسطتها تبادل الطاقة εΔ.
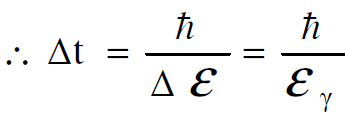 (1.8)
(1.8)
و إذا اعتبرنا ان =1eVεγ فان :
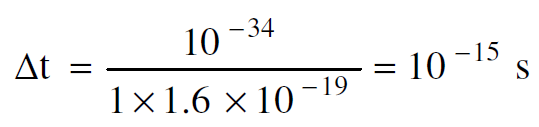 (1.9)
(1.9)
نلاحظ من المعادلة (1.9) ان زمن تبادل الفوتون هو بحدود .10-15s وهكذا فان الفوتونات التي هي بطاقة اقل تحتاج الى زمن اطول للتبادل. ومن الممكن حساب اكبر مسافة تفصل بين الالكترونين Δx كالاتي :
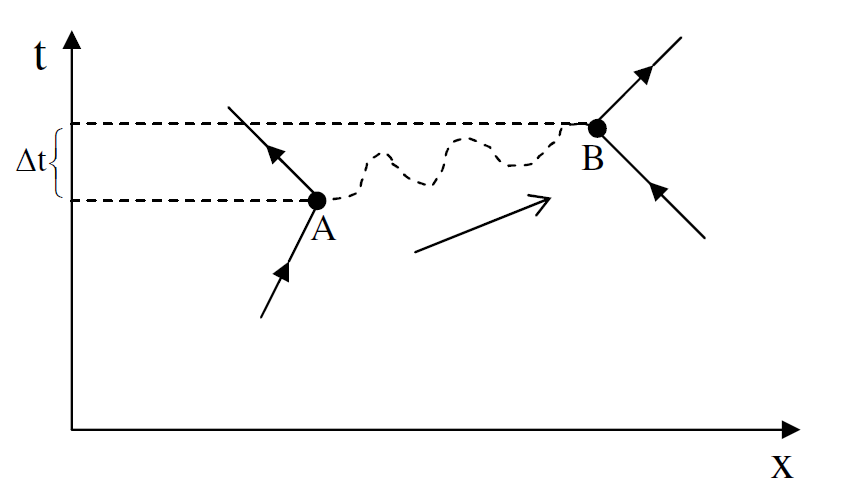
الشكل(1.1) : تبادل الفوتونات خلال التفاعلات الكهرومغناطيسية بين الكترونين.
والجدير بالملاحظة هنا هو أن فوتونات التبادل الوهمية سميت هكذا ذلك لان الفوتونات لا يمكن تحسسها بصورة مباشرة، فالفوتون يتم امتصاصه بواسطة الالكترون B بعد فترة زمنية قصيرة جدًا من لحظة انبعاثه من قبل الالكترونA. وينبغي ان نذكر ان الفوتونات الوهمية لا تخضع لقوانين حفظ الطاقة، لكن وبسبب مبدأ اللايقين وصغر الفترة الزمنية Δt فان الطاقة الزائدة التي يمتلكها الفوتون هي أقل من اللايقين في حساب طاقته الممثلة بالعلاقة Δε ≈ h/Δt.
اما بالنسبة للتفاعلات النووية القوية فسنأخذ بروتون – بروتون او بروتون- نيوترون لكي نوضح كيفية تبادل البايونات خلالها، والشكل (1.2) يوضح ذلك.
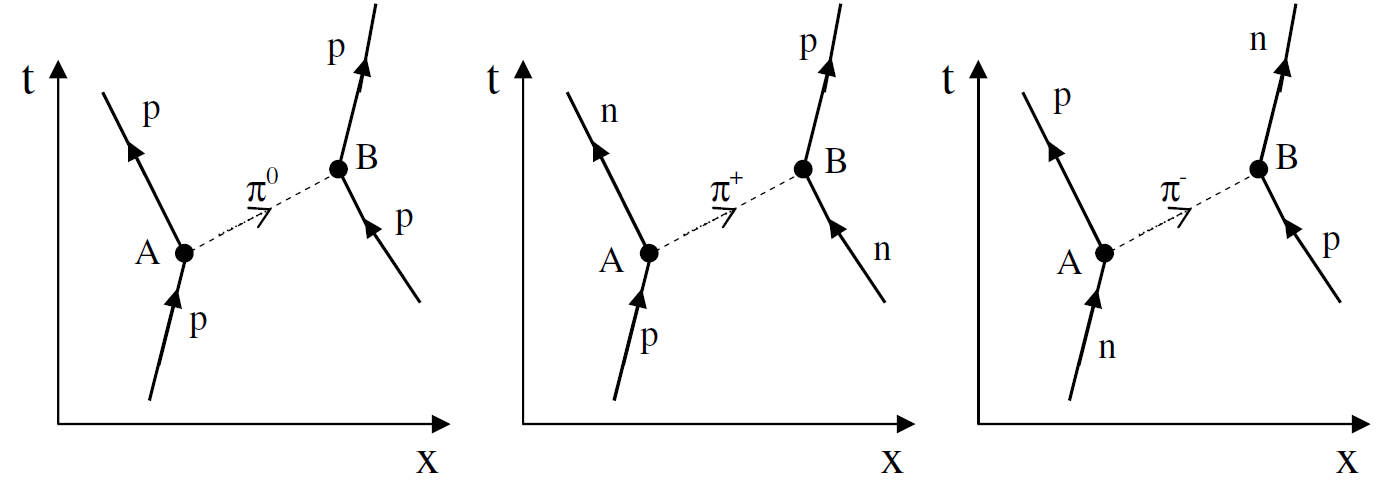
الشكل (1.2) : تبادل البايونات خلال التفاعلات القوية (بروتون – بروتون) و (نيوترون – بروتون) و(بروتون - نيوترون).
من المعروف ان القوة النووية قصيرة المدى لذا فأنها تختلف عن القوة المغناطيسية طويلة المدى. ان القوة النووية تصبح مساوية صفرا في المسافات التي هي اكبر من حوالي (1.4f) لذا فان زمن تبادل البايونات يكون اقصر من زمن تبادل الفوتونات. لو فرضنا ان البايون ينتقل بسرعة الضوء (c) تكون الفترة الزمنية لتبادل البايون بين الجسيمين المتفاعلين مساوية إلى :
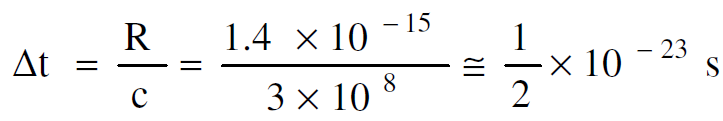
وباستخدام مبدأ اللايقين من الممكن ايجاد الطاقة المتبادلة (Δε):
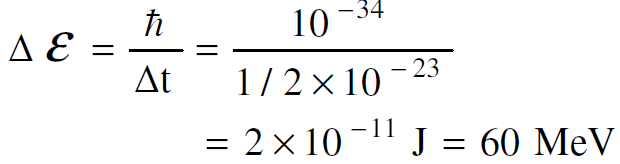
اذن يمكن ايجاد كتلة البايون من العلاقة :
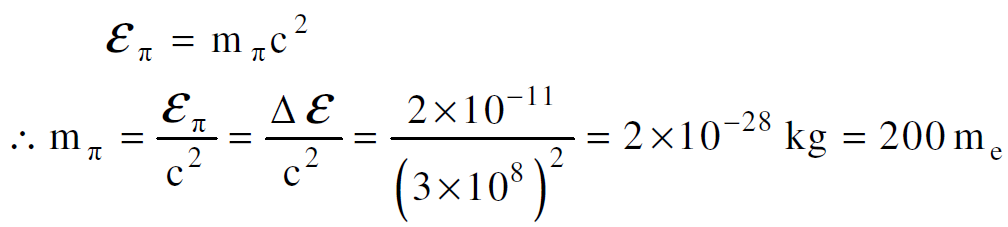
نلاحظ من هذه الحسابات ان للبايون كتلة محددة تساوي 200 مرة بقدر كتلة الالكترون، والجدول (1.4) يبين خصائص البايونات بالتفصيل.
الجدول (1.4) : خصائص البايونات.
ان معظم الجسيمات الاولية غير المستقرة تنحل بواسطة التفاعل الضعيف بأعمار طويلة مقارنة بالتفاعل النووي (23s-10) و البعض الاخر ينحل بواسطة التفاعل الكهرومغناطيسي بأعمار حوالي (10-16s) ومن هذه الجسميات الميونات والبايونات المشحونة والكايونات المشحونة وغير المشحونة وكذلك النيوترون وضديدة والهايبرونات المشحونة وغير المشحونة. والمثال التالي يوضح انحلال K+)) الى بايونين :
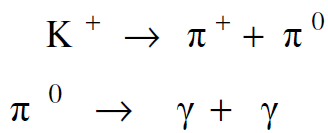
وللسهولة نأخذ الانحلال في محور اسناد يكون فيه الجسيم K+)) في حالة سكون وان المسافة التي يتحرك خلالها الجسيم π0 بسرعة (0.1c) هي :
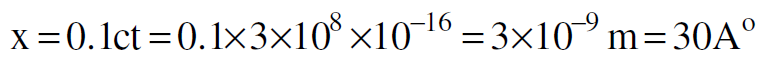
وهذه المسافة صغيرة لا يمكن رؤيتها حتى في حجرة الفقاعة، لذا يظهر الجسيم K+)) الذي ينحل مباشرة الى π+ وفوتونين :
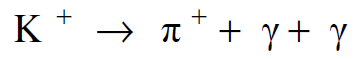
اما البايونات المشحونة فأنها تنحل بواسطة التفاعل الضعيف كما يلي :

وان عمر النصف لكل من π+ و -π هي بحدود 8s)-(2.6×10، اما فانه يتحول الى فوتونين بواسطة التفاعل الكهرومغناطيسي وله عمر نصف بحدود (10-16s).
عندما تنحل الجسيمات الاولية غير المستقرة وهي في حالة سكون أو في حالة حركة، فعملية الانحلال كما لاحظنا يمكن تفسيرها ضمن قوانين حفظ الزخم الخطي وحفظ الكتلة مع الطاقة. ولنعتبر على سبيل المثال جسيما مشحونا هو البايون ( (π+وهو في حالة حركة بسرعة منتظمة v باتجاه الاحداثي x في محور الاسناد s (المحاور المختبرية) كما موضح في الشكل (1.3a). فعندما ينحل هذا الجسيم يتحول الى جسيم مشحون آخر هو الميون ( (π+الذي يصنع الزاوية θ مع الاحداثي x وإلى النيوترينو الميوني (vμ) الذي يصنع الزاوية φ مع الاحداثي x كما في الشكل (1.3b).
ولمعالجة عملية الانحلال هذه ننقل الجسيم المنحل الى محور الاسناد sʹ (محاور مركز الكتلة) الذي يتحرك بسرعة منتظمة v باتجاه الاحداثي x. فقوانين حفظ الزخم في هذا المحور تدل على ان الميون ينبعث باتجاه معاكس لاتجاه النيوترينو ويصنع كل منهما الزاوية α مع الاحداثي x وكما موضح في الشكل (1.4b) بعد الانحلال. اما البايون فهو ساكن في محور الاسناد sʹ قبل الانحلال كما موضح في الشكل (1.4a).
لندرس الان عملية الانحلال في محور الاسناد sʹ وبأعتبار ان (mv, mμ, mπ) هي الكتل الساكنة لكل من البايون والميون والنيوترينو على التوالي وأن εʹv, εʹμ, εʹπ الطاقة الكلية للبايون والميون والنيوترينو على التوالي.
ولنفرض ان زخم الميون يساوي pʹμ وزخم النيوترينو يساوي 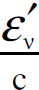 . من قوانين حفظ الزخم نكتب :
. من قوانين حفظ الزخم نكتب :
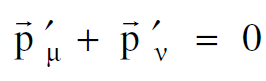 (1.10)
(1.10)
ومن قوانين حفظ الطاقة :
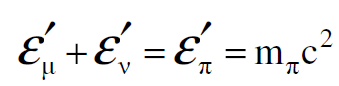 (1.11)
(1.11)
حيث ان :
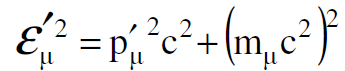 (1.12)
(1.12)
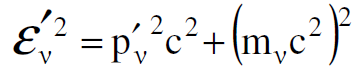 (1.13)
(1.13)
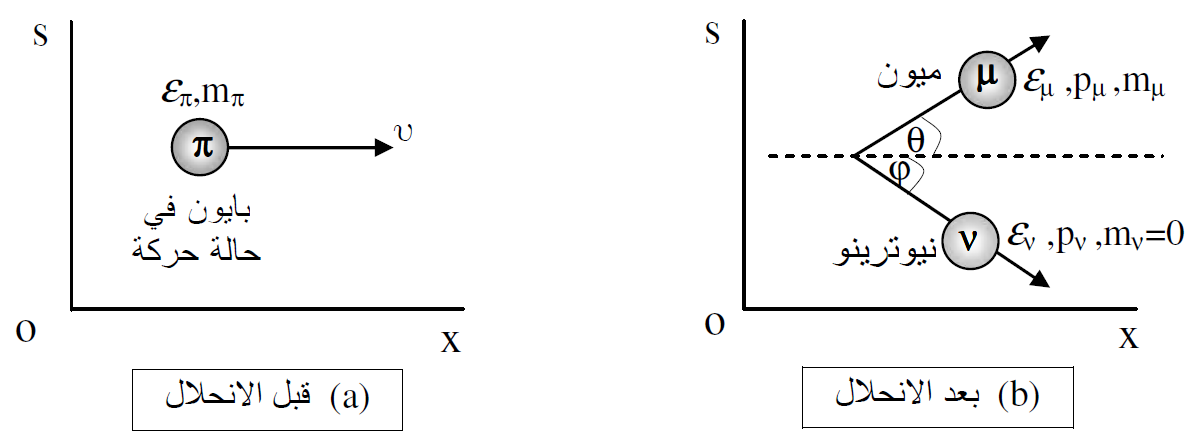
الشكل (1.3) : (a) بايون في حالة حركة بسرعة v قبل الانحلال. (b) يتولد الميون والنيوترينو بعد انحلال البايون.
من المعادلة (1.10) نحصل على :

وبالاستعانة بالعلاقتين (1.12)، (1.13) ينتج أن :
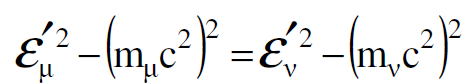
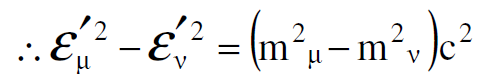 (1.14)
(1.14)
وبحل المعادلتين (1.11)، (1.14) آنياً نحصل على :
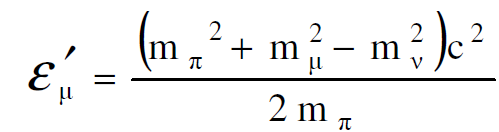 (1.15)
(1.15)
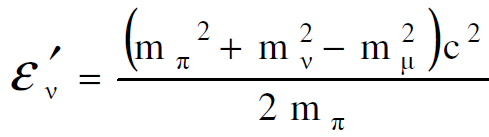 (1.16)
(1.16)
نلاحظ ان المعادلتين الاخيرتين تمثلان الطاقة الكلية لجسيم الميون والنيوترينو على التوالي في محور الاسناد sʹ الذي حدث فيه انحلال جسيم البايون وهو في حالة سكون.
من الممكن الان حساب زخم كل من الميون pʹμ والنيوترينو pʹv في محور الاسناد sʹ فنجد أن :
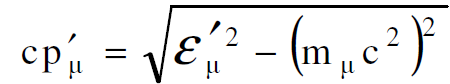 (1.17)
(1.17)
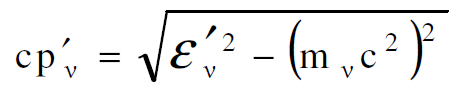 (1.18)
(1.18)
وبما ان:
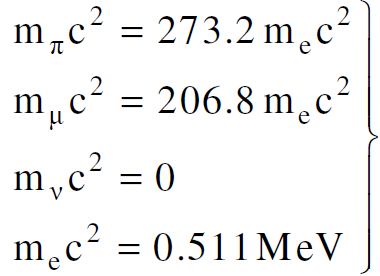
يمكننا حساب الطاقة الحركية Tʹμ للميون والطاقة الحركية Tʹv للنيوترينو وذلك بالاستعانة بالمعادلتين (1.15)، (1.16) فيكون :
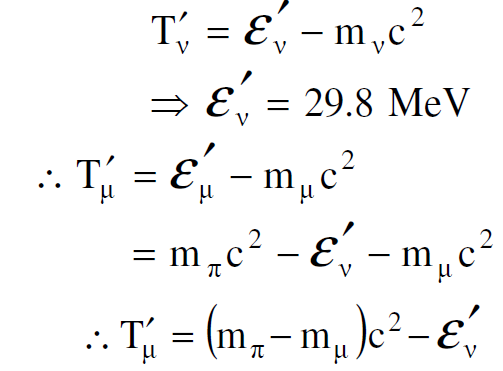
وبتعويض قيم كل من mμc2 ,mπc2 ,εʹv في المعادلة الاخيرة نحصل على :
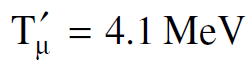
اما زخم كل من المتحررين بعد الانحلال فيمكن حسابه باستخدام المعادلتين (1.17)، (1.18) فيكون :
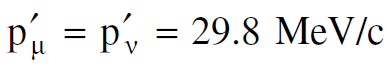
ان الجسيم ( (π+ينحل خلال حركته كما هو موضح في الشكل (1.3)
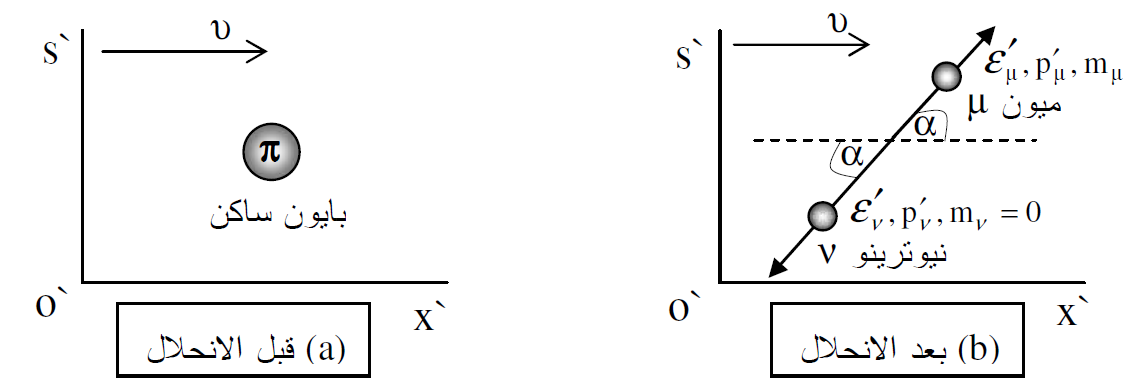
الشكل (1.3) : (a) البايون في حالة سكون قبل الانحلال . (b) بعد انحلال البايون يتولد الميون والنيوترينو باتجاهين متعاكسين وبزخمين متساويين بالمقدار.
اذن يمكن حساب الطاقة الكلية والزخم لكل من الجسيمين المتحررين في محور الاسناد s ( المحاور المختبرية) بعد الاستعانة بمعادلات التحويل للزخم والطاقة من محور الاسناد sʹ الى s وكما يلي :
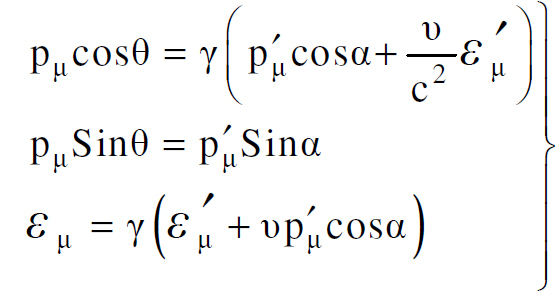 (1.19)
(1.19)
ان الزاوية α التي يصنعها الجسيم ( (μ+ مع الإحداثي xʹ او الجسيم النيوترينو في محور الاسناد sʹ تعتبر عاملا متغيرًا يعود الى نوع الانحلال. ومن الجدير بالذكر ان هذا التحليل يصح بالنسبة لأنحلال اي جسيم غير مستقر الى جسيمين آخرين.
فاذا فرضنا ان m0 الكتلة الساكنة للجسيم المنحل وان m01 و m02 الكتلتان الساكنتان للجسيمين الوليدين من الانحلال، فان المعادلتين (1.15)، (1.16) على سبيل المثال تكتبان بالصيغتين التاليتين :
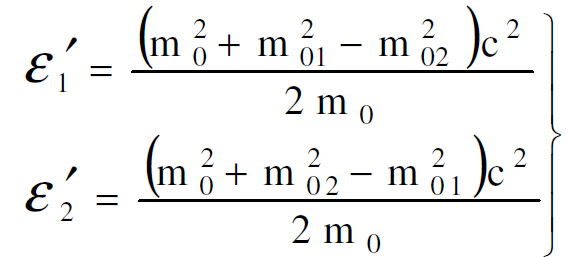 (1.20)
(1.20)



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|