


 الفيزياء الكلاسيكية
الفيزياء الكلاسيكية
 الكهربائية والمغناطيسية
الكهربائية والمغناطيسية
 علم البصريات
علم البصريات
 الفيزياء الحديثة
الفيزياء الحديثة
 النظرية النسبية
النظرية النسبية
 الفيزياء النووية
الفيزياء النووية
 فيزياء الحالة الصلبة
فيزياء الحالة الصلبة
 الليزر
الليزر
 علم الفلك
علم الفلك
 المجموعة الشمسية
المجموعة الشمسية
 الطاقة البديلة
الطاقة البديلة
 الفيزياء والعلوم الأخرى
الفيزياء والعلوم الأخرى
 مواضيع عامة في الفيزياء
مواضيع عامة في الفيزياء| تحويلات المجالات الكهرومغناطيسية الناتجة من الشحنات الكهربائية المتحركة بسرعة ثابتة |
|
|
|
أقرأ أيضاً
التاريخ: 26-4-2016
التاريخ: 21-4-2016
التاريخ: 25-4-2016
التاريخ: 2023-07-02
|
تحويلات المجالات الكهرومغناطيسية الناتجة من الشحنات الكهربائية المتحركة بسرعة ثابتة
من الحقائق المعروفة ان هناك قوة تعتمد على سرعة الشحنات المتحركة. هذه القوة تقترن بمجال مغناطيسي مصدره التيارات الكهربائية او حركة الشحنات. وقد بينت تجربة اورستد ان التيارات الكهربائية تؤثر على المغانط اذا ما قربت منها. بعد ذلك بزمن قليل كشف العالم امبير وآخرون النقاب عن التفاعل بيت التيارات الكهربائية ويتضح ذلك من تجاذب سلكين متوازيين يحمل كل منهما تيارا كهربائية بنفس الاتجاه الذي يحمله الآخر.
نستطيع ان نفهم ما يخص التأثير المغناطيسي للتيارات الكهربائية على أنه نتيجة طبيعية لقانون كولوم او فرضيات النظرية النسبية الخاصة التي اوضحت ان الشحنة تبقى دون تغيير في جميع محاور الاسناد لذا فان التأثيرات المغناطيسية هذه تظهر الى حيز الوجود عندما يحصل تقارن كهربائي بين شحنة متحركة مع شحنات اخرى بالقرب منها.
عندما تتحرك شحنة كهربائية q بالقرب من سلك يحمل تيارا كهربائيا في محور اسناد معين فأنها تتعرض الى مجالين كهربائي ومغناطيسي فتظهر قوة تؤثر عليها تسمى بقوة لورنس كما أوضحت التجارب وتكتب بالصيغة :
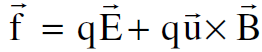 (1.1)
(1.1)
اذ ان  سرعة الشحنة في لحظة معينة وفي موقع ميعن وأن
سرعة الشحنة في لحظة معينة وفي موقع ميعن وأن 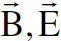 شدة المجال الكهربائي و كثافة الفيض المغناطيسي المتولد عند ذلك الموقع على التوالي.
شدة المجال الكهربائي و كثافة الفيض المغناطيسي المتولد عند ذلك الموقع على التوالي.
لقد تبين ان المغناطيسية تنشأ عن تغيرات نسبية في المجالات الكهربائية للشحنات المتحركة. ويتضح من ذلك ان مركبتي المجالين الكهربائي والمغناطيسي هما مركبتان لكيان واحد. وعليه فان المجال الكهرومغناطيسي يشمل Bx ,By ,Bz ,Ex ,Ey ,Ez وهي ستة مركبات، ويمكن التحسس بوجود المجال في محاور اسناد مختلفة.
نفرض الان جسيما مشحونا يتحرك في محور الاسناد s تحت تأثير مجال كهبائي شدته 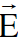 ومجال مغناطيسي كثافة فيضه
ومجال مغناطيسي كثافة فيضه 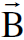 . فاذا كان مقدار الشحنة التي يحملها الجسيم تساوي q فان القوة المؤثرة عليه في هذا المحور تساوي تلك الممثلة بالعلاقة (1) حيث أن
. فاذا كان مقدار الشحنة التي يحملها الجسيم تساوي q فان القوة المؤثرة عليه في هذا المحور تساوي تلك الممثلة بالعلاقة (1) حيث أن 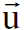 سرعة الجسيم.
سرعة الجسيم.
ولحساب 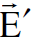 و
و 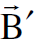 في محور الاسناد sʹ الذي يتحرك بسرعة ثابتة
في محور الاسناد sʹ الذي يتحرك بسرعة ثابتة 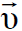 بالاتجاه الموجب للإحداثي xʹ علينا ان نحول القوة
بالاتجاه الموجب للإحداثي xʹ علينا ان نحول القوة 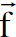 الى ʹ
الى ʹ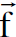 التي تساوي :
التي تساوي :
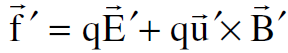 (1.2)
(1.2)
وهذه العلاقة تعطينا التعبير عن  و
و 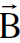 بدلالة ʹ
بدلالة ʹ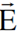 و ʹ
و ʹ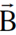 وكذلك
وكذلك 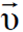 .
.
بعد اجراء عملية فك حاصل الضرب المتجهي 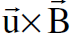 في المعادلة (1.1) من الممكن كتابة مركبات القوة
في المعادلة (1.1) من الممكن كتابة مركبات القوة  باتجاه الإحداثيات المتعامدة x, y, z وكالآتي :
باتجاه الإحداثيات المتعامدة x, y, z وكالآتي :
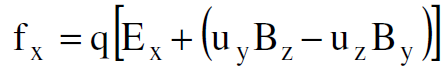 (1.3)
(1.3)
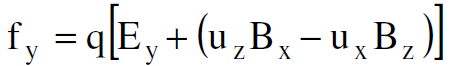 (1.4)
(1.4)
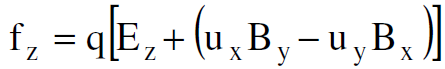 (1.5)
(1.5)
ومن معادلات تحويل القوة من s الى sʹ نجد أن :
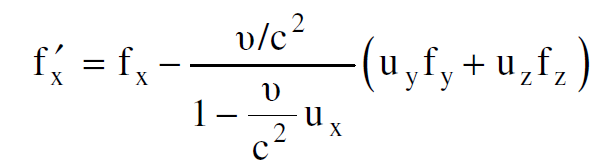 (1.6)
(1.6)
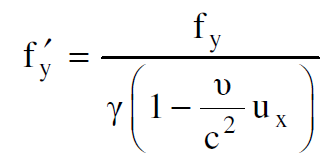 (1.7)
(1.7)
 (1.8)
(1.8)
وتحويلات لورنس المتعلقة بالسرعة تعطي المعادلات الاتية :
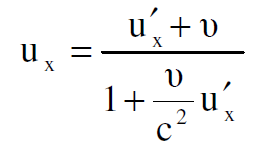 (1.9)
(1.9)
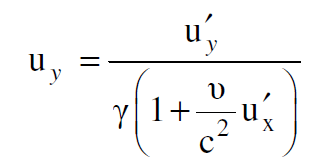 (1.10)
(1.10)
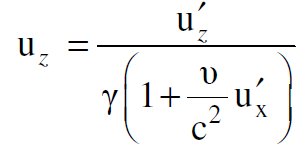 (1.11)
(1.11)
نبدأ الآن بالقوة fʹy كونها بسيطة لأجراء الحسابات والوصول إلى النتيجة المطلوبة. وبعد تعويض قيمة fy من المعادلة (1.4) في المعادلة (1.7) ومن ثم الاستعاضة عن ux و uz بما يساويها من المعادلتين (1.9) ، (1.11) نصل الى التعبير الآتي :
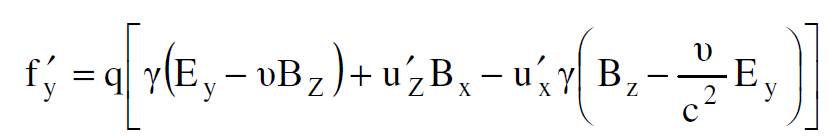 (1.12)
(1.12)
واذا أخذنا المعادلة (1.2) التي تمثل القوة المؤثرة على الجسيم المشحون في محور الاسناد sʹ فان مركبة هذه القوة باتجاه الاحداثي y لا تساوي :
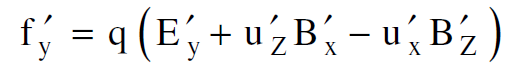 (1.13)
(1.13)
وبمقارنة المعادلتين (1.12) ، (1.13) نستنتج ان :
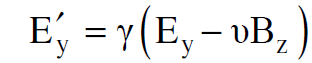 (1.14)
(1.14)
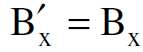 (1.15)
(1.15)
 (1.16)
(1.16)
اذن استطعنا الان ايجاد ثلاثة من ستة مركبات تعود الى المجالين الكهربائي 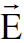 وكثافة الفيض المغناطيسي
وكثافة الفيض المغناطيسي 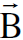 في محور الاسناد sʹ.
في محور الاسناد sʹ.
وباتباع الخطوات السابقة نفسها لمركبة القوة fʹz يعطينا مركبتين أخريين هما :
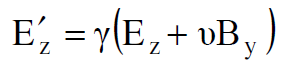 (1.17)
(1.17)
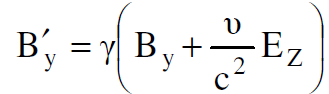 (1.18)
(1.18)
ولإيجاد Eʹx علينا ان نحسب fʹx بعد ان نعتبر الحالة الخاصة الاتية :

اي ان الجسيم المشحون في محور الاسناد s يتحرك باتجاه x. ان هذا الافتراض لا يؤثر على النتيجة التي نحاول الوصول اليها لأن معادلات التحويل الخاصة بالمجالات الكهرومغناطيسية لا تعتمد على سرعة الجسيم ولا على اتجاهه. هذا يعطينا مباشرة معادلة التحويل الأخيرة :
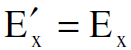 (1.19)
(1.19)
وبإعادة جمع معادلات التحويل هذه تكتب بصورة نهائية كالآتي أولاً من sʹ الى s ثم من s إلى sʹ :
 (1.20)
(1.20)
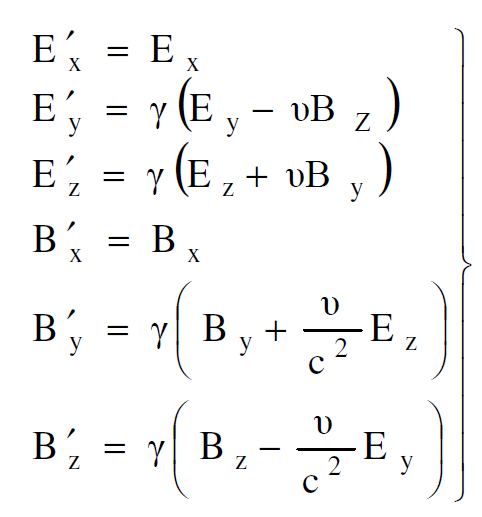 (1.21)
(1.21)
وهكذا نرى ان مركبات 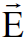 و
و 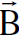 باتجاه الحركة لا تتأثر بالانتقال من محور اسناد الى اخر، الا ان المركبات العمودية على الحركة يحدث لها تغيير كما يظهر من معادلات التحويل التي يمكن اختزالها الى اربع معادلات متجهية.
باتجاه الحركة لا تتأثر بالانتقال من محور اسناد الى اخر، الا ان المركبات العمودية على الحركة يحدث لها تغيير كما يظهر من معادلات التحويل التي يمكن اختزالها الى اربع معادلات متجهية.
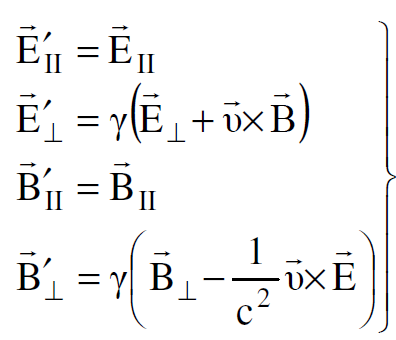 (1.22)
(1.22)
إذ أن ║ و ┴ تعني المركبات الموازية والعمودية على السرعة 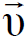 لتحويلات لورنس. اما التحويلات الاخرى من محور الاسناد sʹ الى محور الاسناد s فهي :
لتحويلات لورنس. اما التحويلات الاخرى من محور الاسناد sʹ الى محور الاسناد s فهي :
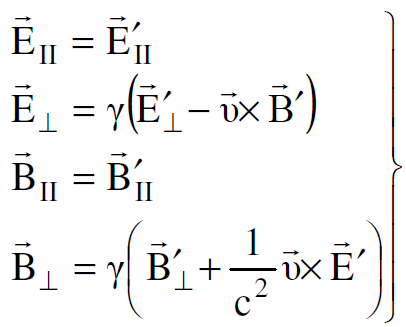 (1.23)
(1.23)
نلاحظ بالنسبة لمشاهد ساكن ان المجال الكهربائي  والمغناطيسي
والمغناطيسي 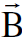 هما كميتان لا تعتمد أحداهما على الاخرى.
هما كميتان لا تعتمد أحداهما على الاخرى.
ولكن لمشاهد في حالة حركة نلاحظ ان المجال الكهربائي يتضمن اجزاء لكلا المجالين الكهربائي  والمغناطيسي
والمغناطيسي 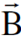 الذين تم تحديدهما من قبل المشاهد الساكن ومن الواضح ان ظهور مجال ما يعتمد على وجه نظر المشاهد في محور اسناد معين وانه لا يوجد تعبير بالمعنى الصحيح يسمى مجال كهربائي خالص او مجال مغناطيسي خالص يمكن اعتباره كيانا قائما بذاته لجميع المشاهدين في جميع محاور الاسناد. فالمجالان الكهربائي والمغناطيسي يوصفان بانهما توأمان متلازمان.
الذين تم تحديدهما من قبل المشاهد الساكن ومن الواضح ان ظهور مجال ما يعتمد على وجه نظر المشاهد في محور اسناد معين وانه لا يوجد تعبير بالمعنى الصحيح يسمى مجال كهربائي خالص او مجال مغناطيسي خالص يمكن اعتباره كيانا قائما بذاته لجميع المشاهدين في جميع محاور الاسناد. فالمجالان الكهربائي والمغناطيسي يوصفان بانهما توأمان متلازمان.
اذا فرضنا الآن ان السرع واطئة (أي v<< c) فان القيمة (/c2 v2) تقترب من الصفر اي ان 1≈γ. ولهذه الحالة الخاصة يتم اختزال معادلات تحويل المجالات الكهرومغناطيسية لتكتب بالصيغة الاتية :
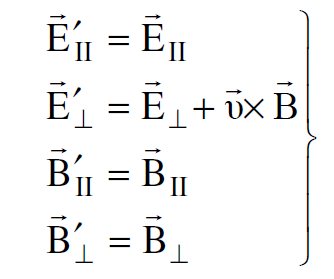 (1.24)
(1.24)
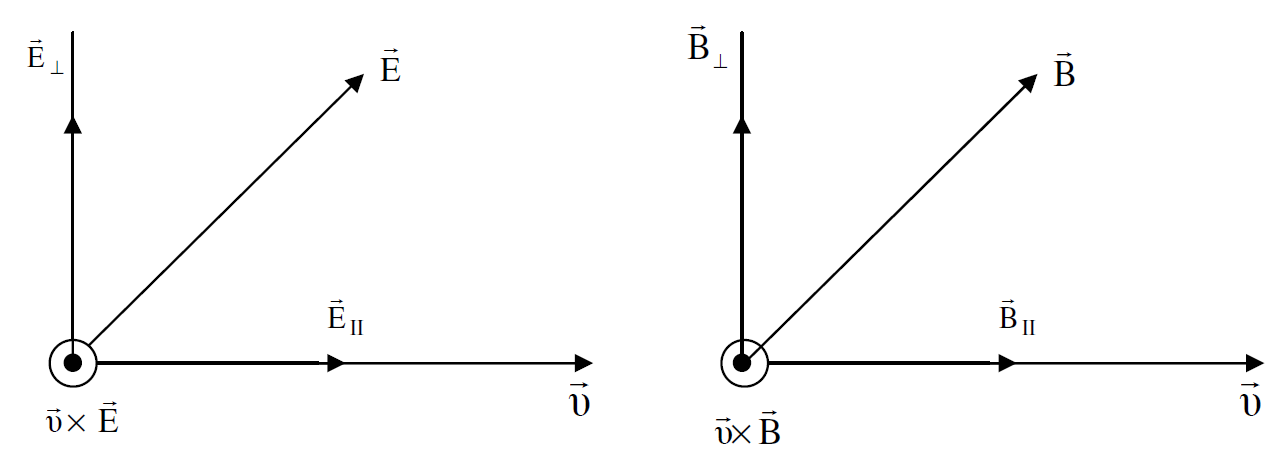
الشكل (1.1) : مركبات المجالين الكهربائي والمغناطيسي باتجاه مواز وعمودي على السرعة v، ويلاحظ اتجاه حاصل الضرب المتجهي بين كل من 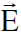 و
و  مع السرعة
مع السرعة 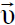 .
.
والشكل (1.1) يبين مركبات المجالين 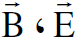 وحاصل ضربهما المتجهي مع
وحاصل ضربهما المتجهي مع  . ولقد وضعنا Ez =Bz=0. مما يجعل
. ولقد وضعنا Ez =Bz=0. مما يجعل  و
و  وكذلك
وكذلك 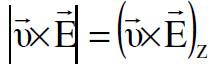 و
و 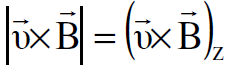 وكما موضح في الشكل، وان
وكما موضح في الشكل، وان 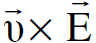 و
و  هما دائما عموديان على
هما دائما عموديان على  .
.



|
|
|
|
للعاملين في الليل.. حيلة صحية تجنبكم خطر هذا النوع من العمل
|
|
|
|
|
|
|
"ناسا" تحتفي برائد الفضاء السوفياتي يوري غاغارين
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|