


 المحاسبة
المحاسبة 
 ادارة الاعمال
ادارة الاعمال
 الادارة
الادارة
 وظيفة التخطيط
وظيفة التخطيط 
 وظيفة التنظيم
وظيفة التنظيم
 وظيفة التوجيه
وظيفة التوجيه 
 وظيفة الرقابة
وظيفة الرقابة 
 ادارة الانتاج
ادارة الانتاج
 ادارة الجودة
ادارة الجودة 
 الادارة الاستراتيجية
الادارة الاستراتيجية
 ادارة التسويق
ادارة التسويق
 ادارة الموارد البشرية
ادارة الموارد البشرية 
 علوم مالية و مصرفية
علوم مالية و مصرفية
 المالية العامة
المالية العامة 
 الاقتصاد
الاقتصاد
 الأحصاء
الأحصاء|
أقرأ أيضاً
التاريخ: 2023-12-10
التاريخ: 5-2-2021
التاريخ: 1-6-2016
التاريخ: 2023-06-08
|
الأساليب النوعية
1- تقديرات رجال البيع: يطالب كل واحد من رجالات البيع بأجراء تقدير عن حجم الطلب على المنتج في المنطقة التي يمارس فيها نشاطه.
مميزات هذه الطريقة:
يسهل عملية التقسيم على حسب المناطق , دقة تنبؤاتهم .
عيوبها:
التأثر بالتحيز الشخصي لرجال البيع.
عدم قدرتهم على التمييز بين رغبات وحاجات الزبائن.
2-أسلوب لجنة الخبراء: يجرى تلخيص آراء مجموعة من الخبراء ممن هم على درجة عالية من المعرفة بهدف الوصول إلى تنبؤ.
3- بحوث السوق: يتطلب القيام بالخطوات الاتية:
تصميم استبانة لجمع البيانات اللازمة عن المستهلكين.
تقرير الكيفية التي ستدار بموجبها الاستبانة.
اختيار عينة ممثلة لمجتمع البحث.
تحليل نتائج الاستبانة.
4- طريقة دلفي: هي عملية الحصول على اتفاق بين آراء مجموعة من الخبراء حول تنبؤ إحدى الحوادث في المستقبل مع المحافظة على سرية هوية كل عضو من أعضاء المجموعة.
الاساليب الكمية:
1-أسلوب تحليل السلاسل الزمنية:
يهدف تحليل السلاسل الزمنية إلى تحديد وعزل كل واحد من العناصر السابقة.
التنبؤ لمدة معينة يعبر عنه كدالة للعوامل السابقة وكالآتي:
حيث إن :
Y = التنبؤ لفترة زمنية ، T = الاتجاه
C = الأثر الدوري. S = الأثر الموسمي.
R = المتغيرات العشوائية.
اهتمامنا سوف يركز على حساب المتوسط والعوامل الموسمية والاتجاه.
2- أسلوب المتوسطات المتحركة البسيطة:
+ وهو من إحدى الطرائق المستخدمة في تحديد الاتجاه في السلسلة ، ويعد أيضاً من أبسط الأساليب الكمية المستخدمة في تنبؤ الطلب على المنتجات.
تنبؤ الطلب لفترة مقبلة = مجموع الطلب لعدد معين من الفترات الماضية / عدد تلك الفترات.
+ لحساب المتوسط المتحرك:

مثال (1-3) : البيانات الآتية تبين الطلب الذي تحقق على المصابيح الكهربائية لشركة النور للأشهر ك / 2 إلى ك / 1 لعام 2009 والمطلوب إجراء تنبؤ للأشهر12 – 5 باستخدام متوسط متحرك طوله 4 أشهر.
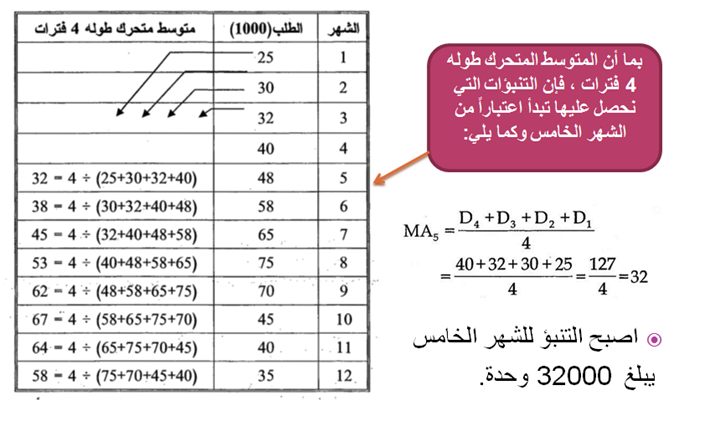
+ التنبؤ للشهر السادس يمكن أجراءه بنفس القاعدة السابقة وذلك بالاعتماد على إحداث أربعة بيانات متوفرة ، أي أن المتوسط المتحرك سيأخذ بالاعتبار الشهر الخامس والرابع والثالث والثاني ويستبعد الشهر الأول من الاعتبار وكما يلي:
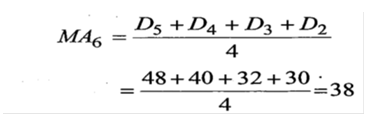
وهكذا، فكلما تتقدم فترة واحدة يجري إسقاط فترة واحدة من الماضي ولهذا السبب تطلق تسمية المتوسطات المتحركة على هذا الأسلوب.
وتفترض هذه الطريقة أن الطلب مستقر نوعاً ما وأنه لا ينطوي على عوامل موسمية .
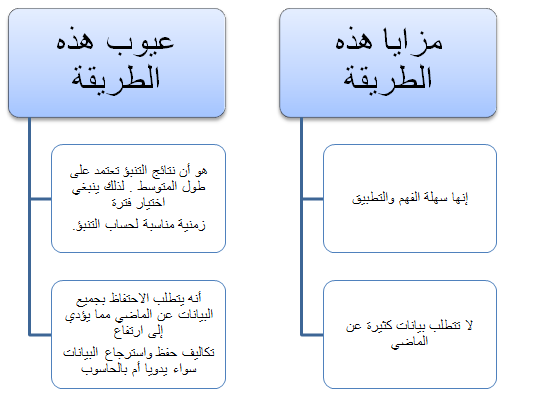
+ هذا الاسلوب يعطي نفس الوزن أو الأهمية لجميع البيانات التي تدخل في حساب التنبؤ
+ الوزن: هو واحد مقسوماً على طول الفترة الزمنية. ويحسب المتوسط المتحرك الموزون بالقاعدة الآتية:

مثال (2-3) : استخدم بيانات الطلب المبينة في مثال ( 1-3) لإجراء تنبؤ للطلب للأشهر12 -5 باستخدام الأوزان التالية:

+ يحسب المتوسط للشهر الخامس كالاتي:
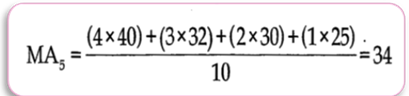
+ أما المتوسط المتحرك للشهر السادس فإنه يأخذ بالاعتبار، أيضاً الطلب الحقيقي للشهر الخامس والرابع والثالث والثاني ويستبعد الشهر الأول. وتطبق الأوزان بنفس الطريقة المتبعة في حساب المتوسط المتحرك للشهر السادس كما يلي:

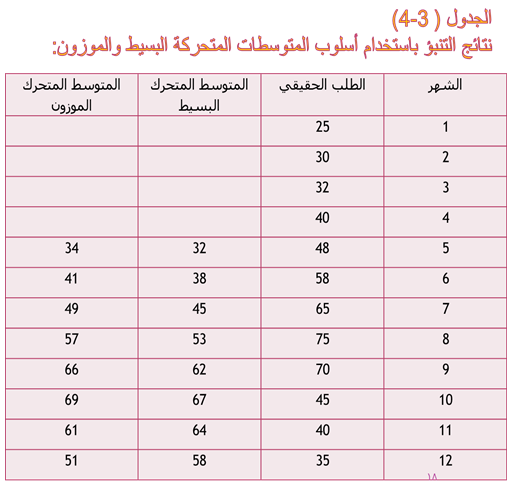
-أسلوب التسريح الاسي البسيط: يعتبر نوع من أنواع المتوسطات المتحركة ويستخدم بكثرة في تنبؤ الطلب على المنتجات والتخزين ويطبق بكفاءة عالية باستخدام الحاسوب وذلك لقلة البيانات الماضية التي يتطلبها هذا الأسلوب، و القاعدة العامة له كالتالي:

ويلاحظ في القاعدة السابقة أن تنبؤ الطلب لفترة معينة يتمثل في التنبؤ للفترة الماضية مضافاً إليه تصحيح الاختلاف بين الطلب والتنبؤ اللذين حدثاً في الفترة الماضية. ويستخدم ثابت التسريح الأسي ((a
في تحديد شدة التصحيح ،أي أن
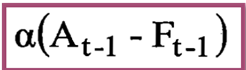
+ فلو كان الطلب الحقيقي أكبر من التنبؤ فإن تصحيح الاختلاف سيكون موجباً، ويكون تصحيح الاختلاف مساوياً إلى صفر عند تساوي الطلب مع التنبؤ، وسالباً إذا كان الطلب أقل من التنبؤ . وتتراوح قيمة (( a بين .50 -.05 في التطبيقات الإدارية للتنبؤ. وبالإمكان زيادة قيمة ((a لتعطي أهمية اكبر لبيانات الطلب الحديثة أو تخفيض قيمة (( a لتعطي أهمية أكبر للبيانات الماضية , ويمكن أيضاً تقدير ((a بالقاعدة التأليه:

وحيث إن N = عدد الفترات التي سنجري لها التنبؤ ويظهر من القاعدة ( ( 4-3 انه لإجراء تنبؤ في المستقبل لا يلزمنا سوى معرفة الطلب الحقيقي والتنبؤ , القاعدة (3-4) يمكن كتابتها بالطريقة الاتية

وبتطبيق هذه القاعدة رجوعا الى الماضي نحصل على الصيغة الاتية :
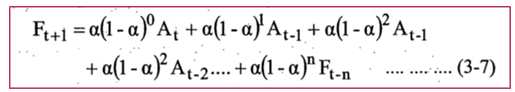
+ فلو فرضنا إن قيمة (a) في القاعدة (3-7) هي 10% فان الوزن الاسي لثلاث فترات ماضية للطلب الحقيقي يحسب كما يلي :

نستنتج مما سبق إن الفترة الحالية تحظى بوزن أسي اكبر من أي فترة أخرى وان أهمية بيانات الطلب تتناقص تدريجيا كلما عدنا الى الماضي .
مثال :
+ ولتطبيق أسلوب التسريح الأسى البسيط نفترض أن تنبؤ الطلب لأحد المنتجات في الشهر الثامن بلغ 150 وحدة وان الطلب الحقيقي لذلك الشهر قد بلغ 170 وحدة , فان تنبؤ الطلب للشهر التاسع باستخدام ثابت تسريح أسي مقداره 0.10 يحسب بقاعدة (4-3) كالاتي :

مثال (3-3) :
+ البيانات التالية تبين الطلب الشهري على احد أنواع الأسمدة الكيماوية , التي تنتجها شركة المشراق , حسب وقوعها في عام 2000 , علما ان تنبؤ الطلب للشهر الأول قد بلغ 135 طن .
+ فما هو تنبؤ الطلب للأشهر التالية باستخدام ثابت تسريح اسي (a) مقداره 0.20 ؟
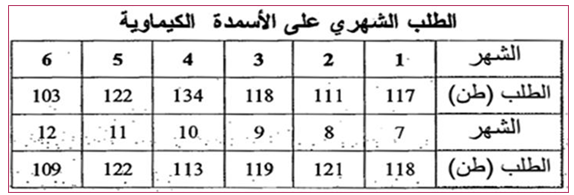
+ وبتطبيق قاعدة (3-4) يمكن الحصول على النتائج التي تظهر في الجدول (3-5).
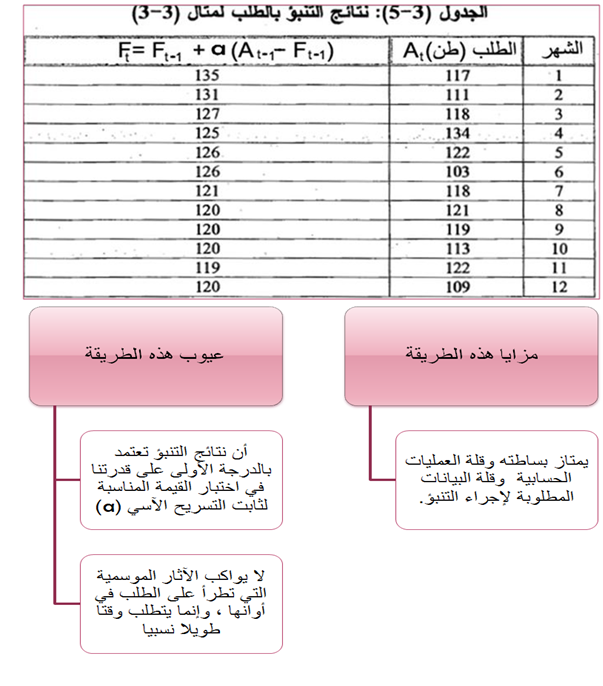

4-أسلوب التسريح الأسى المعدل بالاتجاه: وهو أحد أساليب تنبؤ الطلب الكمية التابع لتحليل السلاسل الزمنية ، ويمتاز عن أسلوب التسريح الأسى البسيط بأنه يأخذ بالاعتبار اتجاه الطلب صعودا أو نزولا.
ملاحظات:
1- يمتاز بالبساطة وقله العمليات الحسابية اللازمة لأجراء التنبؤ.
2- تعتمد نتائج التنبؤ على قدره المحلل في اختيار القيمة المناسبة لثابت التسريح الاسي(a) ولثبات تسريح الاتجاه (b)

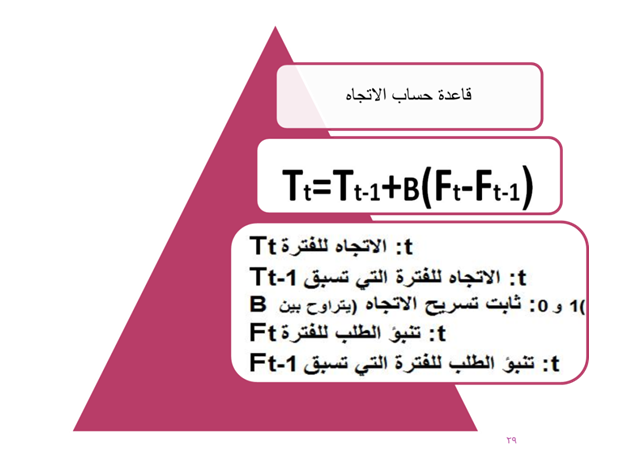
مثال 1: افترض أن الطلب على أحد المنتجات خلال الشهر السادس من عام 2010م بلغ 1000وحدة وأن تنبؤ الطلب لذلك الشهر بلغ 800وحدة ، فما هو تنبؤ الطلب المعدل للشهر السابع ، باستخدام ثابت تسريح أسى 20% وثابت تسريح اتجاه مقداره 30% مع العلم أن الاتجاه للشهر السادس كان 10؟
+ أولاً: نقوم بحساب التنبؤ بطريقة التسريح الأسى البسيط للشهر السابع (Ft=Ft-1+a(At-1-Ft-1 (F7=F6+a(A6-F6 (F7=800+.20(1000-800 وحدة F7= 840
+ ثانياً: نقوم بحساب الاتجاه للشهر السابع (T7=T6+B(F7-F6 T7(T7=10+.30(840-800 = 22
+ ثالثاً: نقوم بحساب التنبؤ المعدل بالاتجاه للشهر السابع FIT7=F7+T7 FIT7=840+22 وحدةFIT7= 862
مثال 2: افترض أن تنبؤ الطلب البسيط للشهر الأول والثاني من عام 2011 م ، بلغ 135 و 131 وحدة على التوالي ، وأن ثبات تسريح الاتجاه مقداره .50 ، قم بإجراء التنبؤ بطريقة التسريح الأسى المعدل للشهر الثاني ، مع افتراض أن الاتجاه للشهر الأول يساوي صفر
+ بما أن المطلوب هو حساب FIT2 وحيث أن F1 و F2 معلومات ، لذا نقوم بحساب T2 ثم ، FIT2
(T2=T1+B(F2-F1 (T2=0+.50(131-135
T2= -2
+ التنبؤ المعدل بالاتجاه هو: FIT2=F2+ T2
( FIT2=131+ (-2 وحدةFIT2= 129
أسلوب خط الاتجاه: وهو أحد أساليب تنبؤ الطلب الكمية التابع لتحليل السلاسل الزمنية ، وتفترض هذه الطريقة أن الطلب على المنتجات يتغير بالزيادة أو النقصان بمرور الزمن ، وأن ما حدث للطلب في الماضي يمكن أن يتكرر في المستقبل.
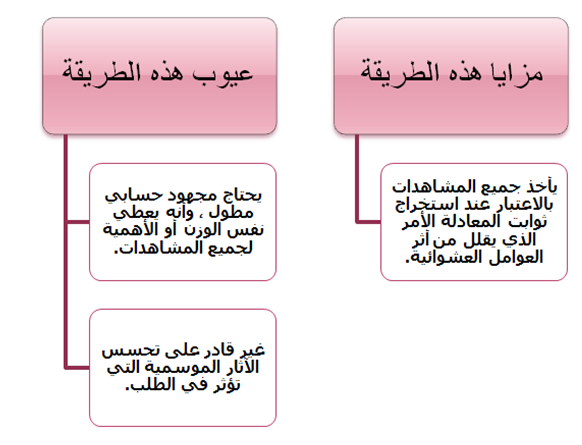
معادلة خط الاتجاه العام لتقدير الطلب في المستقبل:
Y=a + bX +
Y: تنبؤ الطلب
a: ثابت
b: منحنى المعادلة أو درجة ميل المعادلة
(أو الزيادة التي تطرأ على Y بزيادة وحدة واحدة من X)
X: الفترة الزمنية
لتقدير الطلب من خلال معادلة خط الاتجاه نقوم بالخطوات التالية:
1- ترقيم سلسلة السنوات بداية من رقم (1) ثم نقوم بحساب مركز أو الوسط الفرضي للسلسلة. من خلال هذه المعادلة
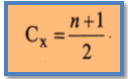
- طرح الوسط الفرضي من رقم كل سنة فنحصل على قيم X
3- وبافتراض أن الطلب يمثل (Y) نقوم بإيجاد قيم (XY)وقيمة وذلك من أجل إيجاد قيمة كل من: و

- ومن خلال معادلة خط الاتجاه: Y=a + bX ، نقوم بالتعويض للحصول على الطلب في فترة زمنية مستقبلية.
مثال:
الجدول التالي يبين الطلب على إطارات السيارات من قياس 175×13 لدى شركة الديوانية لإنتاج الإطارات للأعوام 1989 – 1999 والمطلوب إعداد معادلة خط الاتجاه وتنبؤ الطلب لعام 2000 و2001
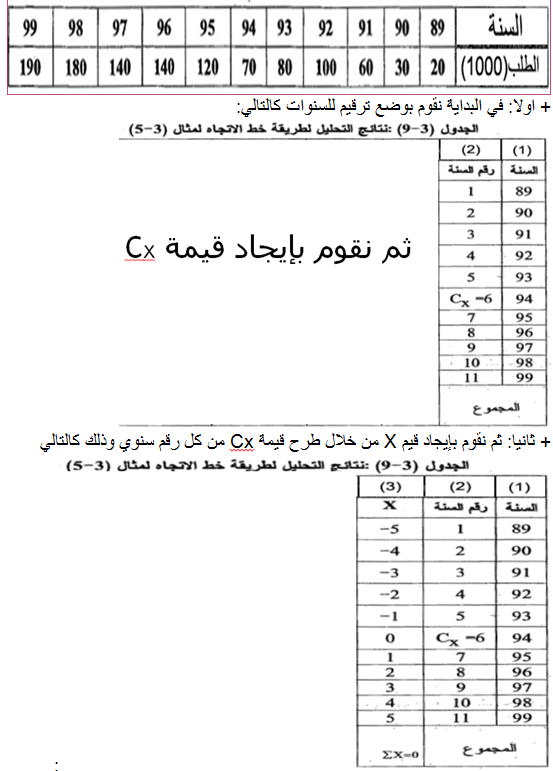
ثالثا: ومن أجل الحصول على قيم (a) و (b) نقوم بإيجاد قيم XY و مع العلم أن Y تمثل الطلب الخاص بالسنوات الماضية وهي معطاة ، وذلك كالتالي:
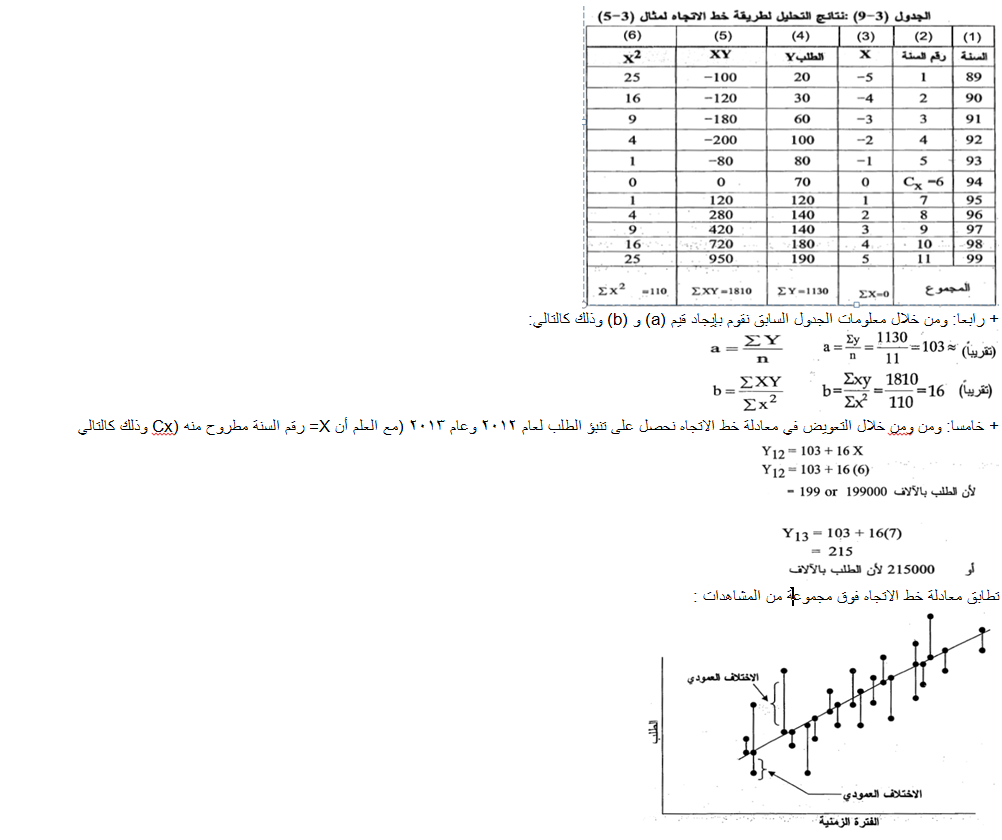



|
|
|
|
مقاومة الأنسولين.. أعراض خفية ومضاعفات خطيرة
|
|
|
|
|
|
|
أمل جديد في علاج ألزهايمر.. اكتشاف إنزيم جديد يساهم في التدهور المعرفي ؟
|
|
|
|
|
|
|
العتبة العباسية المقدسة تقيم ندوة علمية عن روايات كتاب نهج البلاغة
|
|
|