


 الفيزياء الكلاسيكية
الفيزياء الكلاسيكية
 الكهربائية والمغناطيسية
الكهربائية والمغناطيسية
 علم البصريات
علم البصريات
 الفيزياء الحديثة
الفيزياء الحديثة
 النظرية النسبية
النظرية النسبية
 الفيزياء النووية
الفيزياء النووية
 فيزياء الحالة الصلبة
فيزياء الحالة الصلبة
 الليزر
الليزر
 علم الفلك
علم الفلك
 المجموعة الشمسية
المجموعة الشمسية
 الطاقة البديلة
الطاقة البديلة
 الفيزياء والعلوم الأخرى
الفيزياء والعلوم الأخرى
 مواضيع عامة في الفيزياء
مواضيع عامة في الفيزياء|
أقرأ أيضاً
التاريخ: 2023-04-30
التاريخ: 14-2-2017
التاريخ: 2023-05-07
التاريخ: 2023-04-18
|
الشغل المبذول أثناء تغير الحالة الديناميكية الحرارية
لنعتبر أن نظامنا يتكون من كمية من غاز محبوس في أسطوانة مغلقة بكباس قابل للحرجة، كما هو مبين بالشكل 1)). ولنفرض أن الغاز يحمل بالكاد وزن هذا الكباس بحيث يظل ضغط الغاز ثابتاً عند القيمة المعطاة بالعلاقة:

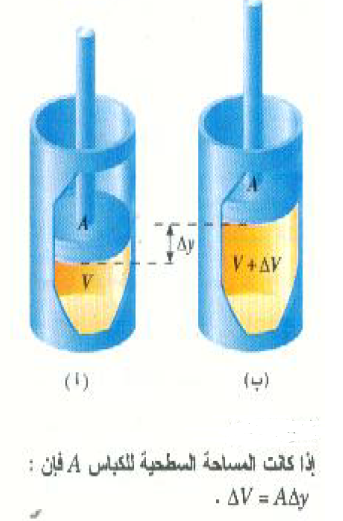
الشكل 1))
لنفرض أن الغاز يتمدد عند تسخينه بمقدار ΔV كما هو مبين بالجزء (ب). أثناء هذا التمدد سوف يرتفع الكباس مسافة Δy، ويكون الشغل المبذول بواسطة الغاز أثناء التمدد (F Δy cos θ) وحيث أن = 0oθ في هذه الحالة إذن:
W = F Δy = PA Δy
وحيث ان A Δyهي الزيادة في حجم الغاز ΔVاذن:
W = P ΔV
وإذا فقدت الحرارة من النظام فإن الغاز ينكمش، وعندئذ تكون ΔV سالبة، وبالتالي يكون الشغل المبذول بواسطة الغاز سالباً أيضاً. وفي تلك الحالة يقال أن الوسط المحيط قد بذل شغلاً على النظام.
ومن الطبيعي أن التمدد عند ثبوت الضغط ما هو إحدى الطرق العديدة التي يمكن أن يتغير بها حجم النظام، وفي حالة ثبوت الضغط يكون حساب الشغل أمراً في غاية البساطة: W = P ΔV. ولكن الشغل يبذل دائماً ( بواسطة النظام أو على النظام) طالما كان هناك تغير في حجم النظام ، وبصرف النظر عن العملية التي يتغير بها الحجم. هذا يوضح بجلاء حاجتنا إلى طريقة عامة لحساب الشغل في كل من العمليات الديناميكية الحرارية، وليس فقط في العمليات ثابتة الضغط. ويمكن تحقيق ذلك بالاستعانة بمنحني الضغط مقابل الحجم، والذي يسمى بالرسم البياني PV (شكل 2))). وتتضح أهمية مثل هذا المنحني في أن أي نقطة على الرسم البياني PV للغاز يمكن حساب درجة الحرارة معينة للغاز. ذلك أنه إذا علمنا قيمتي P و V للغاز
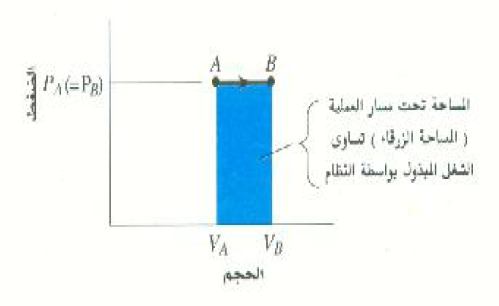
الشكل 2)): الشغل المبذول بواسطة النظام أثناء التمدد عند ثبوت الضغط يساوي المساحة تحت المنحني PV.
حساب درجة الحرارة باستخدام قانون الغاز المثالي.
النقطتان A و B في الشكل 2)) تمثلان حالتين مختلفتين لعينة من غاز عند نفس الضغط PA = PB = P. اما الخط الواصل من A إلى B فيمثل العملية التي تؤدي إلى تغير حلة الغاز ، ويلاحظ أن اتجاه السهم على هذا الخط يوضح الطريقة التي يحدث بها التغير في الحالة. ويوضح الخط الأفقي المستقيم أن التغير يحدث عند ثبوت الضغط. وتجدر الإشارة في هذه النقطة إلى أنه يمكن توصيل النقطة A بالنقطة B بعدد لا نهائي من المسارات التي يمثل كل منها عملية ديناميكية حرارية مختلفة، وبالتالي كمية مختلفة من الشغل.
نحن نعلم الآن حساب الشغل أثناء العملية ثابتة الضغط الموضحة بالشكل 2)):
= P(VB – VA) W = P ΔV
لاحظ أن P(VB – VA) هي المساحة تحت الخط AB، أي مساحة المستطيل الأزرق بالشكل 2)). لنفترض الآن أن الغاز يمر بعملية انضغاط من الحالة B إلى الحالةA . عندئذ سيكون VΔ، ومن ثم W، سالباً، مما يشير إلى أن الشغل يبذل على النظام في هذه الحالة. وحيث أن المساحة تحت الخط لم تتغير ، من الضروري إذن استخدام الإشارة الجبرية الصحيحة وذلك بملاحظة ما إذا كان الحجم يزداد (+) أو يقل (-).
لنعمم الآن هذه النتيجة. اعتبر العملية الاختيارية ( الاعتباطية ) الممثلة بالمنحني AB في الشكل (3). في مثل هذه الحالة تتغير الكميات T ، V ، P كلها أثناء العملية، ولكن المنطقة ذات اللون الأزرق الغامق في الشكل تمثل جزءاً صغيراً جداً من العملية، صغيرة إلى درجة تكفي لاعتبار الضغط ثابتاً اثناءها. وهكذا فإن الشغل المبذول في هذا الجزء من العملية يساوي P ΔV. ولإيجاد الشغل الكلي المبذول خلال العملية من A إلى B كلها، يمكننا النظر إلى هذه العملية كما لو كانت مكونة من عدد كبير جداً من مثل هذه التغيرات الحجمية الصغيرة، والتي يبذل خلالها كل منها كمية من الشغل تساوي المساحة المحصورة تحت المنحني PV الخاص بها. وليه فإن الشغل الكلي المبذول يساوي مجموع هذه المساحات الغيرة؛ أي المساحة المحصورة تحت المنحني من A إلى B ( المساحة الملونة باللون الأزرق الفاتح). وهكذا يستنتج أن:
الشغل المبذول أثناء تغير الحالة الديناميكية الحرارية يساوي المساحة المحصورة تحت منحني العملية في الرسم البياني PV.
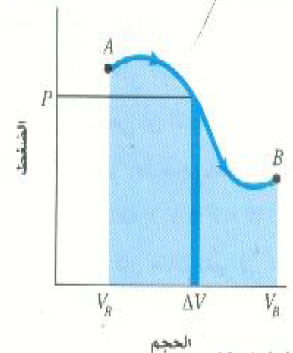
الشكل 3)): الشغل المبذول بواسطة النظام عند انتقاله من الحالة A إلى الحالة B بأي عملية ديناميكية حرارية يساوي المساحة المحصورة تحت المنحني PV الذي يمثل العملية.
ويكون الشغل موجباً عند زيادة الحجم نتيجة للعملية الديناميكية الحرارية، ويكون سالباً عند نقصه.



|
|
|
|
لصحة القلب والأمعاء.. 8 أطعمة لا غنى عنها
|
|
|
|
|
|
|
حل سحري لخلايا البيروفسكايت الشمسية.. يرفع كفاءتها إلى 26%
|
|
|
|
|
|
|
جامعة الكفيل تحتفي بذكرى ولادة الإمام محمد الجواد (عليه السلام)
|
|
|