


 الفيزياء الكلاسيكية
الفيزياء الكلاسيكية
 الكهربائية والمغناطيسية
الكهربائية والمغناطيسية
 علم البصريات
علم البصريات
 الفيزياء الحديثة
الفيزياء الحديثة
 النظرية النسبية
النظرية النسبية
 الفيزياء النووية
الفيزياء النووية
 فيزياء الحالة الصلبة
فيزياء الحالة الصلبة
 الليزر
الليزر
 علم الفلك
علم الفلك
 المجموعة الشمسية
المجموعة الشمسية
 الطاقة البديلة
الطاقة البديلة
 الفيزياء والعلوم الأخرى
الفيزياء والعلوم الأخرى
 مواضيع عامة في الفيزياء
مواضيع عامة في الفيزياء|
أقرأ أيضاً
التاريخ: 27-6-2016
التاريخ: 20-9-2020
التاريخ: 20-9-2020
التاريخ: 23-7-2016
|
الانسياب الطبقي مقابل الانسياب المضطرب
لنتفحص الآن كيفية انسياب السوائل في المواسير. عندما يتحرك سائل في ماسورة تحاول قوى الاحتكاك التي تؤثر بها جدران الماسورة على السائل أن تكبح انسياب السائل، مثلها في ذلك مثل قوى اللزوجة داخل السائل. ونتيجة لذلك سوف ينساب السائل الملاصق للجدران بسرعة حركة السائل القريب من منتصف الماسورة. ويوضح الشكل (1 أ) هذه الظاهرة، حيث تمثل أطوال الأسهم مقدار السرعة في المواضع المختلفة في الأنبوبة.
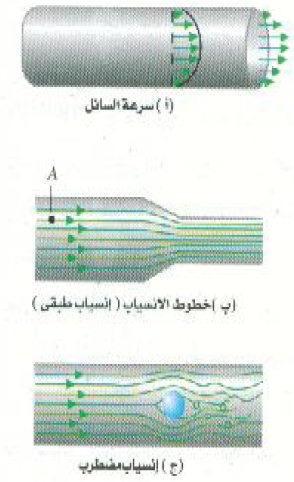
الشكل 1)): أمثلة للملامح المختلفة للانسياب في ماسورة: (أ) جانبية السرعة، (ب) الانسياب الطبقي، (جـ) الانسياب المضطرب.
ويمثل الشكل (1 ب) سمة أخرى لانساب سائل في ماسورة . لنفرض أن ذرة دقيقة من التراب ، لتلك الذرة الموجودة عند النقطة A ، تنساب مع السائل إذا كان معدل الانسياب منخفضاً سوف تتبع هذه الذرة الخط الموضح أثناء حركتها داخل الماسورة. كذلك فإن الذرات الترابية الأخرى، والسائل أيضا، سوف تتبع خطوطاً ملساء مشابهة. ويطلق على هذه الخطوط اسم خطوط الانسياب، ويسمى هذا النوع من انسياب السوائل بالانسياب الطبقي. إذن ، في الانسياب الطبقي بتبع كل عنصر من السائل خط انسياب تكراري معين.
أما إذا كان مقدار سرعة الانسياب كبيراً سوف يحدث تغير حاد في نسق الانسياب. فبدلاً من أن تكون خطوط الانسياب ملساء ناعمة فإنها ستصبح خطوطاً ملتوية مضطربة كما هو مبين بالشكل 1)جـ)، ويعرف هذا النوع من الانسياب باسم الانسياب المضطرب. وفي هذه الحالة تكون فواقد الطاقة الاحتكاكية ( او اللزوجة) أكبر مما في حالة الانسياب الطبقي، وهذا بدوره يسبب زيادة المقاومة الاحتكاكية على الأسطح المتلامسة مع السائل المنساب. وتجدر الإشارة في هذا المقام أن قانون بوازيل لا ينطبق في حالة الانسياب المضطرب.
ليس من الضروري ان يكون السائل (او المائع عموماً) محصوراً في ماسورة لكي يحدث هذان النوعان من الانسياب ، إذ يشاهد هذا السلوك عند انسياب المائع على أي سطح مثل جناح الطائرة أو الأسطح الخارجية لهيكل السيارة. ونظراً لزيادة الاحتكاك المرتبطة ببداية الاضطراب يحاول مصممو السيارات والطائرات تصميم أسطح الطائرات والسيارات بحيث تقل التأثيرات الاضطرابية إلى الحد الادنى، ولهذا يكون ابتكار طريقة للتنبؤ ببداية الاضطراب على قدر كبير من الأهمية من الناحية العملية.
عندما يكون انسياب السائل حول الجسم طبقياً، تتناسب القوة المثبطة او قوة المقاومة، FD تناسباً خطياً مع مقدار سرعة الانسياب v. ومع ذلك فإن حساب قوة المقاومة رياضياً عملية صعبة عموماً، ولذلك فإنها تقاس عادة بالطرق العملية. فمثلاً، تستخدم أنفاق الرياح لقياس قوى المقاومة الناتجة عند انسياب الهواء على أسطح السيارات والطائرات. وفي عام 1843 استطاع الفيزيائي الإنجليزي ج. ستوكس استنتاج علاقة بين FD و v في حالة كرة نصف قطرها r تتحرك بسرعة صغيرة في مائع لزوجته η، و تعرف هذه العلاقة بقانون ستوكس:
FD = 6πηrv
أما في حالة السرعات العالية بدرجة كافية لحدوث الانسياب المضطرب فإن قوة المقاومة لا تتناسب ببساطة مع مقدار السرعة، بل انها تمثل بمتسلسلة معقدة بدلالة السرعة مرفوعة إلى أسس أعلى. وقد وجد في معظم الحالات المتعلقة بالسيارات والطائرات أن FD تتناسب طردياً مع 2v:
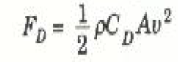
حيث A المساحة الأمامية للسيارة أو الطائرة ؛ ويعرف الثابت اللابعدي CD بمعامل مقاومة الهواء. ويمثل الجدول 1)) بعض قيم معامل مقاومة الهواء لبعض الاجسام. وبالرغم من أن معالجة الأنسياب المضطرب رياضياً مسألة في غاية الصعوبة، فإن هناك مفهوماً موحداً يبسط الموقف بدرجة كبيرة. ذلك أن التجربة قد أثبتت أن الانسياب الطبقي يتول إلى انسياب مضطرب عندما تصل قيمة ثابت لا بعدي يسمى عدد رينولدز NR إلى قيمة حرجة معينة، ويعطي عدد رينولدز بالعلاقة:
NR = ρvd/η
حيث ρ، v، η كثافة المائع ومقدار سرعة انسيابه ولزوجته على الترتيب؛ d بعد مميز لنظام الانسياب وهو يتوقف على التطبيق المعني في كل حالة على وحدة. فمثلاً، عندما يحدث انسياب وهو يتوقف على التطبيق المعنى في كل حالة على حدة. فمثلاً، عندما يحدث انسياب المائع في ماسورة يكون d هو نصف قطر الماسورة؛ وفي حالة حركة كرة في مائع يكون d هو قطر الكرة؛ وإذا كان الجسم غير منتظم الشكل كالطائرة مثلاً ، يكون d هو متوسط أبعاد الطائرة. ويمثل الجدول 2)). بعض الأمثلة لأعداد رينولدز الحرجة.
الجدول 1)): القيم النمطية لمعامل مقاومة الهواء المقاسة باستخدام نفق الرياح.
|
الجسم |
معامل مقاومة الهواء |
|
لوح مسطح |
1.2 |
|
السابح في الهواء ( ممتد أفقياً) |
1.0 |
|
دراجة نارية وراكبها |
0.9 |
|
سيارة ( سيدان) |
0.5 |
|
سيارة رياضية ( ذات خطوط انسيابية) |
0.25 |
|
قطار ذو خطوط انسيابية |
0.15 |
|
ظاهرة الانتقال |
NR |
|
ــ القيمة العظمى لعدد رينولدز NR للانسياب الطبقي حول كرة ( قانون ستوكس). |
10 |
|
ــ بداية الاضطراب في ماسورة أسطوانية ذات مدخل غير منتظم. |
1000-1200 |
|
ــ بداية الاضطراب في ماسورة أسطوانية طويلة ( حد صلاحية قانون بوازيل). |
2000-3000 |
|
ــ بداية الاضطراب في المواسير ذات مدخل مزود بمنفث ملائم. |
20,000 – 40,000 |
|
ــ الحد العلوي عندما يتبع سلوك الانسياب العلاقة FD α v2 |
3×105 |
وبالرغم من ان القيم الحرجة لعدد ربنولدز تفتقر إلى الدقة فإنها نافعة جداً في تعيين ما يسمى قوانين المقياس النسبي . فمثلاً ، إذا كان لدينا نظامان أحدهما نموذج مطابق للآخر بمقياس رسم معين فإن نمطي انسيابهما سيكونان متطابقين إذا كانت قيمتي NR لهما متساويتان . ويقال لثل هذين النظامين أنهما متشابهان ديناميكياً . هذا المفهوم هو الأساس الفيزيائي لاختبارات أنفاق الرياح التي تجري على نماذج مطابقة مصغرة للسيارات والطائرات . ويكون نمطا الانسياب متشابهين عند تساوي حاصل الضرب vd (ومن ثم NR). وعليه فإن الانسياب البطيء (v صغيرة) لمائع حول جسم كبير ( d كبير) سيطابق انسياب نفس المائع بضعف السرعة حول جسم أصغر مرتين .



|
|
|
|
دراسة: حفنة من الجوز يوميا تحميك من سرطان القولون
|
|
|
|
|
|
|
تنشيط أول مفاعل ملح منصهر يستعمل الثوريوم في العالم.. سباق "الأرنب والسلحفاة"
|
|
|
|
|
|
|
الطلبة المشاركون: مسابقة فنِّ الخطابة تمثل فرصة للتنافس الإبداعي وتنمية المهارات
|
|
|