


 الفيزياء الكلاسيكية
الفيزياء الكلاسيكية
 الكهربائية والمغناطيسية
الكهربائية والمغناطيسية
 علم البصريات
علم البصريات
 الفيزياء الحديثة
الفيزياء الحديثة
 النظرية النسبية
النظرية النسبية
 الفيزياء النووية
الفيزياء النووية
 فيزياء الحالة الصلبة
فيزياء الحالة الصلبة
 الليزر
الليزر
 علم الفلك
علم الفلك
 المجموعة الشمسية
المجموعة الشمسية
 الطاقة البديلة
الطاقة البديلة
 الفيزياء والعلوم الأخرى
الفيزياء والعلوم الأخرى
 مواضيع عامة في الفيزياء
مواضيع عامة في الفيزياء|
أقرأ أيضاً
التاريخ: 13-11-2020
التاريخ: 11-7-2016
التاريخ: 2024-02-04
التاريخ: 15-11-2020
|
الانكماش النسبوي للطول
تقتضي ظاهرة تمديد الزمن وجود ظاهري غريبة تتعلق بالأطوال المقاسة. نعتبر أن سيدة مستقرة على الأرض بينما يسافر الرجل بسرعة مقدارها v على طول خط مستقيم يمتد من الأرض إلى النجم ألفاً سنتورى. ويفيدنا رجال الفلك الموجودون على الأرض أن النجم يبعد عن الأرض مسافة مقدارها d = 4.1×1016m.
وحيث أنه من السهل قياس السرعات النسبية، فإن كلاً من الرجل والسيدة متفقان على أن سرعة كل منهما بالنسبة للآخر هي v عندما أخذ الرجل في الانطلاق داخل سفينة الفضاء من الأرض نحو النجم. أما السيدة فهي ساكنة في مناط إسناد تكون فيه الأرض والنجم أيضاً في سكون أنها ترى أن الرجل يمرق أمامها بسرعة مقدارها v.
الرجل ساكن بالنسبة لسفينته الفضائية ويعتبر السفينة نفسها هي مناط إسناده. وكل من الأرض والنجم يعتبران في حركة بسرعة مقدارها v بالنسبة للسفينة.
دعنا الآن نفحص رحلة الرجل من الأرض إلى النجم من واقع أفضلية السيدة.
إنها تعلم أن المسافة من الأرض إلى النجم، وكلاهما في سكون بالنسبة لمناط إسنادها هي de = 4.1×1016m ، حيث يرمز الحرف e إلى الأرض. وباستعمال العلاقة x = vt فإنها ستحسب الزمن الذي تسجله الساعة الأرضية لرحلة الرجل نحو النجم على أنه :

وبالفعل، حين تستدير السفينة عائدة إلى الأرض بعد أن بلغت النجم، فإن الزمن استغرقته الرحلة كلها سيكون 2te = 2de/v.
إلا أن حسابات الرجل ستكون مختلفة فحسب الساعات الموجودة بسفينة الفضاء سيكون زمن الرحلة من الأرض إلى النجم هو ts. ومن ثم يستطيع أن يحسب المسافة إلى النجم على أنها x = vt ويصل إلى:
ds = vts
حيث يشير الحرف s إلى القياسات التي تمت في مناط إسناد ساكن بالنسبة لسفينة الفضاء وبإجراء حسابات مماثلة لرحلة العودة فإنه يجد أن الرحلة بأكملها قد قطعت مسافة 2ds في زمن مقداره 2ts.
وعلى ذلك يصبح لدينا المعادلتان التاليتان وهما صحيحتان دون أدنى شك بالنسبة للراصدين اللذين صاغهما :

ولكننا نعرف أن التمديد الزمني يؤثر على ساعة سفينة الفضاء، بحيث أننا لو قارناها بالساعة الأرضية عند عودة السفينة إلى الأرض فسنجد أن:
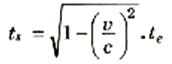
أي أن ساعة سفينة الفضاء قد طقطقت الزمن بشكل أبطأ من الساعة الأرضية. وبالتعويض من هذه القيمة للزمن ts في معادلة ds نجد أن:
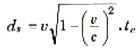
على أن de = vte ولذلك فإن te = de/v وإذا استخدمنا هذه القيمة للزمن te فإن:
وحيث أنه من السهل قياس السرعات النسبية، فإن كلاً من الرجل والسيدة متفقان على أن سرعة كل منهما بالنسبة للآخر هي v عندما أخذ الرجل في الانطلاق داخل سفينة الفضاء من الأرض نحو النجم. أما السيدة فهي ساكنة في مناط إسناد تكون فيه الأرض والنجم أيضاً في سكون أنها ترى أن الرجل يمرق أمامها بسرعة مقدارها v.
الرجل ساكن بالنسبة لسفينته الفضائية ويعتبر السفينة نفسها هي مناط إسناده. وكل من الأرض والنجم يعتبران في حركة بسبب مقدارها v بالنسبة للسفينة.
دعنا الآن نفحص رحلة الرجل من الأرض إلى النجم من واقع أفضلية السيدة.
إنها تعلم أن المسافة من الأرض إلى النجم، وكلاهما في سكون بالنسبة لمناط إسنادها هي de = 4.1×1016m، حيث يرمز الحرف e إلى الأرض. وباستعمال العلاقة x = vt فإنها ستحسب الزمن الذي تسجله الساعة الأرضية لرحلة الرجل نحو النجم على أنه:

وبالفعل، حيث تستدير السفينة عائدة إلى الأرض بعد أن بلغت النجم، فإن الزمن الذي استغرقته الرحلة كلها سيكون 2te = 2de/v.
إلا أن حسابات الرجل ستكون مختلفة فحسب الساعات الموجودة بسفينة سيكون زمن الرحلة من الأرض إلى النجم هو ts ومن ثم يستطيع ان يحسب المسافة إلى النجم على أنها x = vt ويصل إلى:
ds = vts
حيث يشير الحرف s إلى القياسات التي تمت في مناط إسناد ساكن بالنسبة لسفينة الفضاء وبإجراء حسابات مماثلة لرحلة العودة فإنه يجد أن الرحلة بأكملها قد قطعت مسافة 2ds في زمن مقداره 2ts.
وعلى ذلك يصبح لدينا المعادلتان التاليتان وهما صحيحتان دون أدنى شك بالنسبة للراصدين اللذين صاغهما:

ولكننا نعرف أن تمديد الزمن يؤثر على ساعة سفينة الفضاء، بحيث أننا لو قارناها بالساعة الأرضية عند عودة السفينة إلى الأرض فسنجد أن:
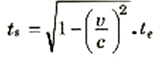
أي أن ساعة سفينة الفضاء قد طقطقت الزمن بشكل أبطأ من الساعة الأرضية. وبالتعويض من هذه القيمة للزمن ts في معادلة ds نجد أن:
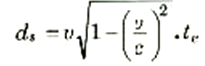
على أن de = vte ولذلك فإن te = de/v. وإذا استخدمنا هذه القيمة للزمن te فإن:
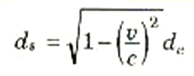
وبعبارة أخرى فإن المسافة بين الأرض والنجم. . إذا قيست بساعة الرجل في سفينته الفضائية ستكون أقصر من المسافة التي يقيسها الفلكيون وهم على سطح الأرض. فمن الظاهر إنه كنت تتحرك بالنسبة لنقطتين بينهما مسافة ثابتة، فإن المسافة بين النقطتين ستبدو أقصر مما لو كانت ساكناً بالنسبة لهما. والنسبة بين المسافتين هي معامل النسبية، 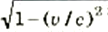 .
.
لقد وجد أينشتين أن هذه نتيجة عامة، ويمكننا تلخيصها كما يلي:
لو أن جسماً وراصداً كانا في حركة نسبية بسرعة مقدارها v، فإن الراصد سيقيس طول الجسم المتحرك كما لو كان قد انكمش على طول خط الحركة بعامل مقداره 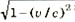 .
.
يلاحظ أن الانكماش لا يحدث سوى باتجاه خط الحركة، ولا يلاحظ أي انكماش عمودياً على خط الحركة. ويسمى طول جسم ما إذا قيس بواسطة راصد ساكن بالنسبة للجسم الطول الصحيح.



|
|
|
|
هل تعرف كيف يؤثر الطقس على ضغط إطارات سيارتك؟ إليك الإجابة
|
|
|
|
|
|
|
جهد إعلامي متألق وثّق مراسم الزيارة الرجبية
|
|
|