


 الفيزياء الكلاسيكية
الفيزياء الكلاسيكية
 الكهربائية والمغناطيسية
الكهربائية والمغناطيسية
 علم البصريات
علم البصريات
 الفيزياء الحديثة
الفيزياء الحديثة
 النظرية النسبية
النظرية النسبية
 الفيزياء النووية
الفيزياء النووية
 فيزياء الحالة الصلبة
فيزياء الحالة الصلبة
 الليزر
الليزر
 علم الفلك
علم الفلك
 المجموعة الشمسية
المجموعة الشمسية
 الطاقة البديلة
الطاقة البديلة
 الفيزياء والعلوم الأخرى
الفيزياء والعلوم الأخرى
 مواضيع عامة في الفيزياء
مواضيع عامة في الفيزياء|
أقرأ أيضاً
التاريخ: 19-9-2020
التاريخ: 27-6-2016
التاريخ: 27-6-2016
التاريخ: 3-7-2016
|
قانون هوك وطاقة الجهد المرن
أن كثيرا من الانظمة المرنة (الشبيهة بالزنبركات) تتبع قانون هوك الذي ينص على أن القوة الشوهة تتناسب مع التشوه الذي تسببه ، وفي حالة زنبرك يستطيل تحت تأثير قوة مسلطة Fapp كما بالشكل 1)) فإن الإزاحة x التي يستطيل بها الزنبرك ترتبط بالقوة Fapp تبعا للعلاقة :
(1) Fapp= kx
حيث k مقدار ثابت يسمى ثابت الزنبرك , ووحداته في النظام si هي النيوتن لكل متر. وثابت الزنبرك مقياس "لكزازة" الزنبرك , فكلما زادت قيمة ثابت الزنبرك، كلما زادت القوة اللازمة لإطالة الزنبرك بمقدار محدد.
ويوضح الشكل ( 1ب) كيف تتغير القوة مع تشوه الزنبرك الموضح بالشكل (1 أ). هذا المنحني عبارة عن خط مستقيم ميله يساوي k طبقا للمعادلة ((1 (قانون هوك). لنحاول الآن حساب الطاقة المختزنة في زنبرك ممتد أو منضغط يتبع قانون هوك.
يمكننا إثبات أن الشغل المبذول لإطالة الزنبرك من x = 0 الى x = x0 يساوي المساحة تحت الخط المستقيم المبين بالشكل (1 ب). ولتحقيق ذلك يمكننا ملاحظة أن مساحة المستطيل المظلل بالشكل تساوي Fi Δxi حيث Fi هي قوة المطيلة أثناء الزيادة الصغيرة في التشوه xiΔ وحيث W = Fs Δs , إذن هذه المساحة أيضا الشغل المبذول بواسطة قوة المطيلة أثناء هذه الزيادة الصغيرة في الإزاحة. فإذا تخطينا أن المنطقة الموجودة تحت الخط المستقيم من x = 0 الى x = x0 مملوءة بعدد كبير جدا من مثل هذه المستطيلات. فإن مجموع مساحات هذه المستطيلات يعطينا الشغل المبذول أثناء إطالة الزنبرك من x = 0 الى x = x0 إذن:
الشغل المبذول في إطالة أو ضغط عنصر من يساوي المساحة المحصورة تحت الخط البياني الذي يمثل F مقابل x.
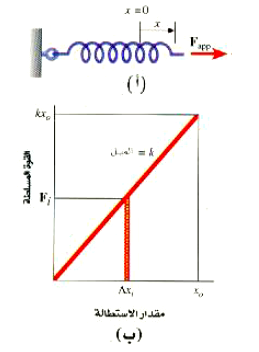
الشكل 1)): لكي يستطيل الزنبرك بمقدار معين يجب ان تسلط عليه قوة خارجية مساوية ومضادة لقوة الاستعادة المؤثرة بواسطة الزنبرك. ونظراً لأن قوة الاستعادة تتناسب مع مقدار الاستطالة x ، فإن Fapp - x، وهذا مبين بالجزء (ب)، والشغل المبذول بواسطة Fapp يساوي المساحة الواقعة تحت منحني Fapp مقابل x .
عند استخدام الرسم البياني PV لتعيين الشغل المبذول بواسطة غاز عندما يتغير حجمه ، وعليك إثبات ان ذلك صحيح أيضا في حالة انضغاط الزنبرك .
وحيث أن مساحة المثلث تساوي نصف حاصل ضرب طول قاعدته في ارتفاعه، إذن يمكننا أن نرى من الشكل 1)) أن المساحة الواقعة تحت الخط البياني تساوي (½x0)(kx0). ولكن هذه المساحة تساوى الشغل المبذول في إطالة الزنبرك ؛ ولذلك فهي تساوي طاقة الجهد المختزنة في الزنبرك , بناء على ذلك يستنتج أن طاقة الجهد المختزنة في زنبرك ثابتة k عند استطالته ا, انضغاطه مسافة قدرها ء تساوي :
2)) 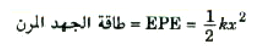
والآن وقد تمكنا من إيجاد الطاقة المرنة المختزنة في زنبرك (او أي نظام يتبع قانون هوك) ، يمكننا استخدام قانون بقاء الطاقة لكي نعلم الكثير عن اهتزاز النظام. لقد فرضنا في تلك الحالة أن فواقد الاحتكاك مهملة . وهذا يعني طبقا لقانون بقاء الطاقة أن مجموع طاقة الجهد المختزنة في الزنبرك وطاقة حركة الكتلة يجب أن يظل ثابتا. وللتعبير عن هذا المعنى في صورة معادلة رياضية لنعد مرة أخرى الى النظام لحظة إعتاق الكتلة من الموضع x = x0 . والآن ، حيث ان الطاقة الكلية الابتدائية للنظام في تلك الخطة تساوي kx20 ½، فإن طاقته الكلية في أي لحظة زمنية تالية تكن:
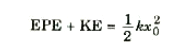
وبالتعويض نجد أن :
3)) 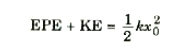
حيث m و v تعود على الكتلة المثبتة في الزنبرك فقط , لأننا نفترض أن كتلة الزنبرك نفسه مهملة. لاحظ أن x0 تمثل هنا سعة الحركة .
والمعادلة 3))، رغم بساطتها ، أداة فعالة جدا في مناقشة الحركة الاهتزازية , ويمكن استخدامها لإيجاد سرعة الكتلة عند أي نقطة x في مسار الحركة:
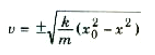
لا تحفظ هذه المعادلة لأنها هي نفس المعادلة 3)) بعد إعادة ترتيب حدودها. لاحظ أن v = 0 عند x = x0، أي عندما تكون الكتلة في نهاية الاهتزازية , وأن السرعة تصل الى أكبر قيمة لها ، 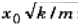 ، عند x = 0. ومع أننا نعمل هذه الحقائق من مناقشتنا الوصفية للتحول المتبادل للطاقة بين طاقتي الحركة والوضع، فغننا نستطيع الآن إيجاد سرعة الكتلة المهتزة عند أي موضع x .
، عند x = 0. ومع أننا نعمل هذه الحقائق من مناقشتنا الوصفية للتحول المتبادل للطاقة بين طاقتي الحركة والوضع، فغننا نستطيع الآن إيجاد سرعة الكتلة المهتزة عند أي موضع x .
يتبقى علينا الان إيجاد علجة الكتلة المهتزة. عندما يهتز النظام اهتزازا حرا يكون الموقف كما هو مبين بالشكل 2)) ، وكما نرى من الشكل فإن القوة الوحيدة غير المتزنة المؤثرة على الكتلة هي شد الزنبرك لها F ، وهذه القوة تسمى قوة الاستعادة لأنها تؤثر دائما في اتجاه يعمل على جذب او دفع النظام الى موضع اتزانه. ومع أن مقدار F يساوي kx ، أي نفس القوة اللازمة لإطالة الزنبرك بمقدار x , إلا أن اتجاهها مضاد لاتجاه الاستطالة , وبذلك تكون قيمتها F = -kx حيث تشير الإشارة السالبة الى أن هذه قوة استعادة ، أي قوة تؤثر في اتجاه مضاد للإزاحة x . وحيث أن F هي القوة غير المتزنة المؤثرة على الكتلة , يمكننا ان نجد من العلاقة F = ma. أن عجلة الكتلة تعطى بالمعادلة:
4)) 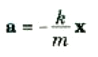
لا حظ أن مقدار العجلة يصل الى قيمته العظمى عند x = ±x0 لان قوة الاستعادة تكون أكبر ما يمكن في هذين الموضعين , أما عند x = 0 فإن الاستعادة تكون صفرا، وتكون العجلة بالتالي صفرا. وهكذا نرى أنه يمكننا استعمال المعادلتين (3) و((4، لإيجاد سرعة وعجلة الكتلة عند أي إزاحة x.
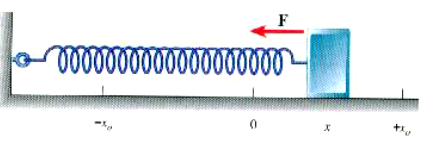
الشكل 2)): القوة التي بها الزنبرك على الكتلة هي قوة استعادة تعطى بالعلاقة F = -kx.



|
|
|
|
دراسة: حفنة من الجوز يوميا تحميك من سرطان القولون
|
|
|
|
|
|
|
تنشيط أول مفاعل ملح منصهر يستعمل الثوريوم في العالم.. سباق "الأرنب والسلحفاة"
|
|
|
|
|
|
|
الطلبة المشاركون: مسابقة فنِّ الخطابة تمثل فرصة للتنافس الإبداعي وتنمية المهارات
|
|
|