Cube’s Apparent Rotation
المؤلف:
Sidney B. Cahn And Boris E. Nadgorny
المصدر:
A GUIDE TO PHYSICS PROBLEMS
الجزء والصفحة:
part 1 , p 35
13-7-2016
1619
Cube’s Apparent Rotation
A cube with 1-meter edges in its rest frame moves along a straight line at velocity βc. An observer is located in the laboratory frame, and the distance of closest approach is much greater than 1 m. Two faces of the cube are perpendicular to the direction of motion and another two faces are parallel to the plane formed by the trajectory and the observer. The other two faces are approximately perpendicular to the line of sight of the observer (see Figure 1.1). In this problem, we need to take into account the different travel times for light from different parts of the cube to the observer. This effect causes distortions which make the cube appear to the observer to be rotated. Find the expression for the apparent rotation and indicate the sign of the rotation with respect to the direction of motion of the cube and the line from the cube to the observer.
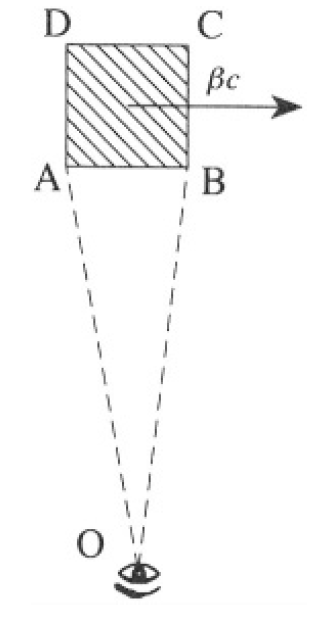
Figure 1.1
SOLUTION
At any given moment, the image of the cube is created by the photons reaching the observer at this time. The light received from points A and B of the near face of the cube is accompanied by light from point D emitted a time (1/c) earlier (see Figure 1.2a). The length of
is Lorentz contracted to
while the distance from A' to A is β (the distance the
Figure 1.2a Figure 1.2b
cube has moved while the light from D travelled to the front face). The apparent rotation is seen in Figure 1.2b. The angle of rotation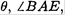 
should be equal to 
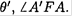From the figure, we see that 
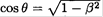and sin θ' = β. So θ = θ', and the cube does appear rotated by sin-1 β. A more detailed solution of this problem employs the Lorentz transformation from frame K' to K of the velocities which leads to the light aberration seen by the observer O.
الاكثر قراءة في مواضيع اخرى
اخر الاخبار
اخبار العتبة العباسية المقدسة
