


 الفيزياء الكلاسيكية
الفيزياء الكلاسيكية
 الكهربائية والمغناطيسية
الكهربائية والمغناطيسية
 علم البصريات
علم البصريات
 الفيزياء الحديثة
الفيزياء الحديثة
 النظرية النسبية
النظرية النسبية
 الفيزياء النووية
الفيزياء النووية
 فيزياء الحالة الصلبة
فيزياء الحالة الصلبة
 الليزر
الليزر
 علم الفلك
علم الفلك
 المجموعة الشمسية
المجموعة الشمسية
 الطاقة البديلة
الطاقة البديلة
 الفيزياء والعلوم الأخرى
الفيزياء والعلوم الأخرى
 مواضيع عامة في الفيزياء
مواضيع عامة في الفيزياء|
Read More
Date: 6-9-2016
Date: 13-7-2016
Date: 21-8-2016
|
Cube Bouncing off Wall
An elastic cube sliding without friction along a horizontal floor hits a vertical wall with one of its faces parallel to the wall. The coefficient of friction between the wall and the cube is μ. The angle between the direction of the velocity v of the cube and the wall is α. What will this angle be after the collision (see Figure 1.1 for a bird's-eye view of the collision)?
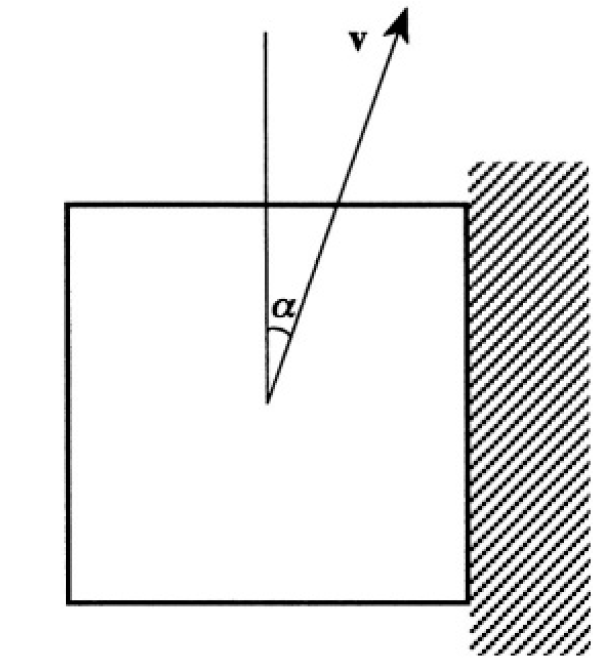
Figure 1.1
SOLUTION
There are two forces acting on the cube. One is the normal reaction N(t), perpendicular to the wall, and the other is the force of friction Ffr(t), parallel to the wall (see Figure 1.2). We expect that, as a result of the collision, the cube’s velocity v will change to v'. In the direction perpendicular to
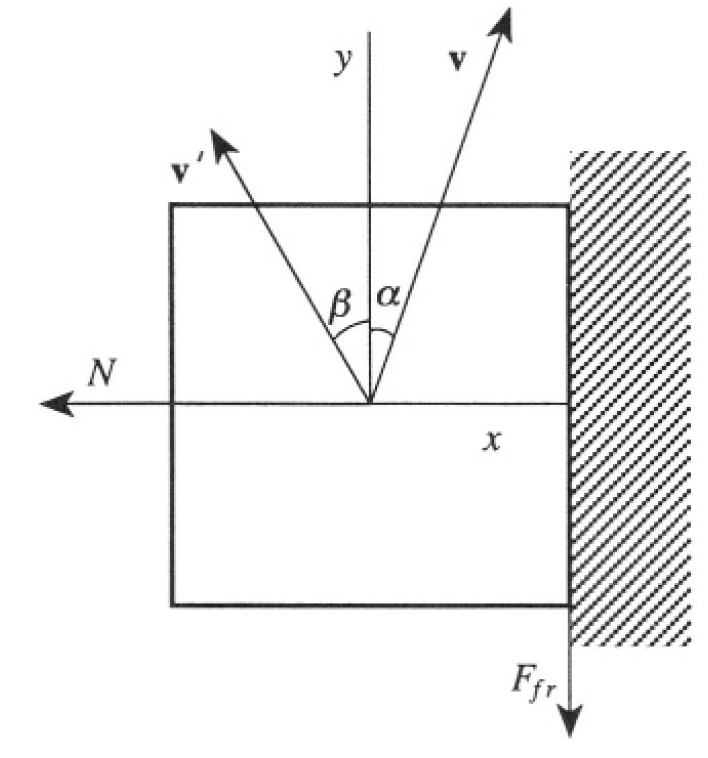
Figure 1.2
the wall, the collision is elastic, i.e., the velocity in the  direction merely changes sign: v'x = -vx = -v sin α. Therefore, the momentum changes by -2mv sinα in
direction merely changes sign: v'x = -vx = -v sin α. Therefore, the momentum changes by -2mv sinα in  the direction. This change is due to the normal reaction N(t). So, according to Newton’s second law:
the direction. This change is due to the normal reaction N(t). So, according to Newton’s second law:
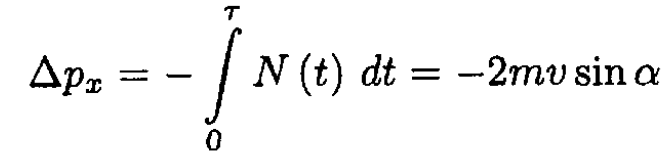 (1)
(1)
Where τ is the collision time. If there were no friction, the parallel velocity component would not change and the angle would remain the same. However, in the actual case, the ŷ component changes and
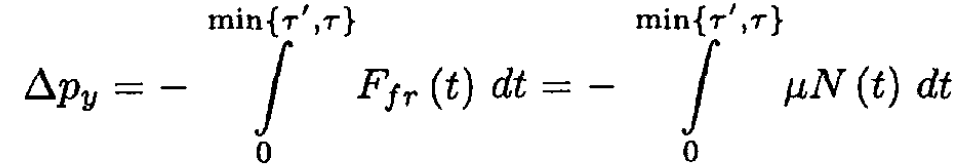 (2)
(2)
Here τ' is the time at which the velocity vy goes to zero. So, from (2)
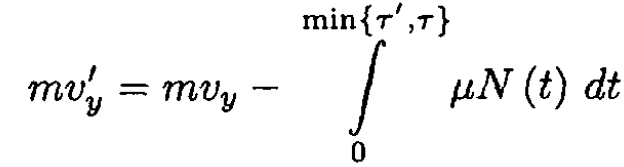 (3)
(3)
First assume that τ < τ', i.e., v'y is not zero. Then we have from (1)
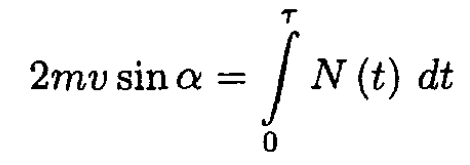
and
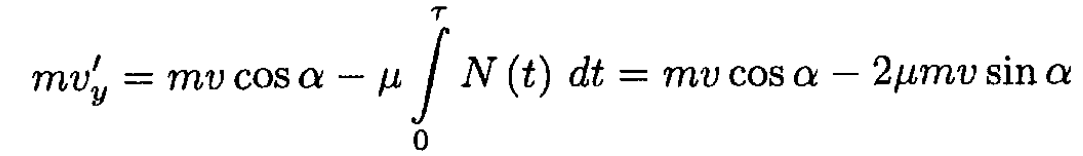
or

Therefore, the angle β between the velocity v' and the wall is given by
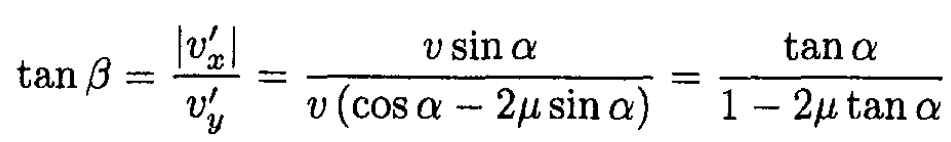
If 1-2μ tanα = 0, then tanα = (1/2μ) and tanβ goes to infinity, which corresponds to β = π/2. Now if 1-2μ tanα < 0 (vy goes to zero before the collision ends; v'y cannot become negative), then τ > τ', and the cube will leave perpendicular to the wall. Therefore,
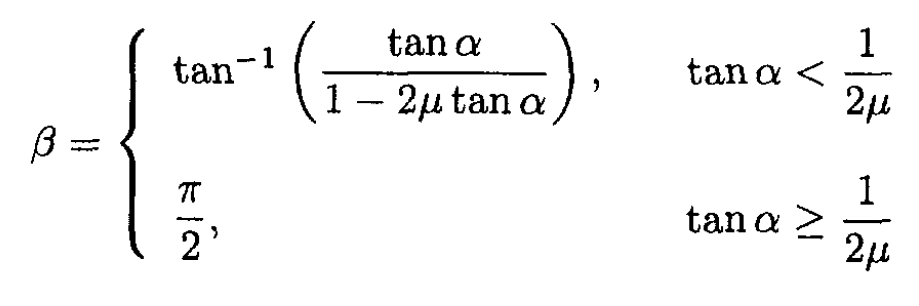



|
|
|
|
دراسة تحدد أفضل 4 وجبات صحية.. وأخطرها
|
|
|
|
|
|
|
جامعة الكفيل تحتفي بذكرى ولادة الإمام محمد الجواد (عليه السلام)
|
|
|