
تاريخ الفيزياء

علماء الفيزياء


الفيزياء الكلاسيكية

الميكانيك

الديناميكا الحرارية


الكهربائية والمغناطيسية

الكهربائية

المغناطيسية

الكهرومغناطيسية


علم البصريات

تاريخ علم البصريات

الضوء

مواضيع عامة في علم البصريات

الصوت


الفيزياء الحديثة


النظرية النسبية

النظرية النسبية الخاصة

النظرية النسبية العامة

مواضيع عامة في النظرية النسبية

ميكانيكا الكم

الفيزياء الذرية

الفيزياء الجزيئية


الفيزياء النووية

مواضيع عامة في الفيزياء النووية

النشاط الاشعاعي


فيزياء الحالة الصلبة

الموصلات

أشباه الموصلات

العوازل

مواضيع عامة في الفيزياء الصلبة

فيزياء الجوامد


الليزر

أنواع الليزر

بعض تطبيقات الليزر

مواضيع عامة في الليزر


علم الفلك

تاريخ وعلماء علم الفلك

الثقوب السوداء


المجموعة الشمسية

الشمس

كوكب عطارد

كوكب الزهرة

كوكب الأرض

كوكب المريخ

كوكب المشتري

كوكب زحل

كوكب أورانوس

كوكب نبتون

كوكب بلوتو

القمر

كواكب ومواضيع اخرى

مواضيع عامة في علم الفلك

النجوم

البلازما

الألكترونيات

خواص المادة


الطاقة البديلة

الطاقة الشمسية

مواضيع عامة في الطاقة البديلة

المد والجزر

فيزياء الجسيمات


الفيزياء والعلوم الأخرى

الفيزياء الكيميائية

الفيزياء الرياضية

الفيزياء الحيوية

الفيزياء العامة


مواضيع عامة في الفيزياء

تجارب فيزيائية

مصطلحات وتعاريف فيزيائية

وحدات القياس الفيزيائية

طرائف الفيزياء

مواضيع اخرى
Double Collision of Mass–Spring System
المؤلف:
Sidney B. Cahn And Boris E. Nadgorny
المصدر:
A GUIDE TO PHYSICS PROBLEMS
الجزء والصفحة:
part 1 , p 13
28-7-2016
3525
Double Collision of Mass–Spring System
A ball of mass M moving with velocity V0 on a frictionless plane strikes the first of two identical balls, each of mass m = 2kg connected by a massless spring with spring constant k = 1kg/s2 (see Figure 1.1). Consider the collision to be central and elastic and essentially instantaneous.
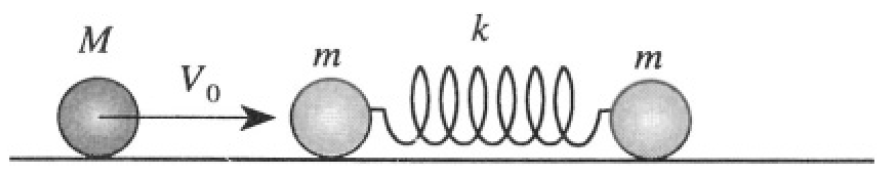
Figure 1.1
a) Find the minimum value of the mass M for the incident ball to strike the system of two balls again.
b) How much time will elapse between the two collisions?
SOLUTION
a) Let us call the ball of mass M ball 1, the first ball struck 2, and the third ball 3 (see Figure 1.2a). After the first collision, ball 1 will move with constant velocity V1 and balls 2 and 3 will oscillate. For another collision to take place, the coordinates of balls 1 and 2 must coincide at some later moment. First find V1 after the initial collision, considered to be instantaneous. Then, this problem is no different from the collision of just two balls of masses M and m. If the velocity of the first ball before the collision is V0 we can find V1 and V2 from energy and momentum
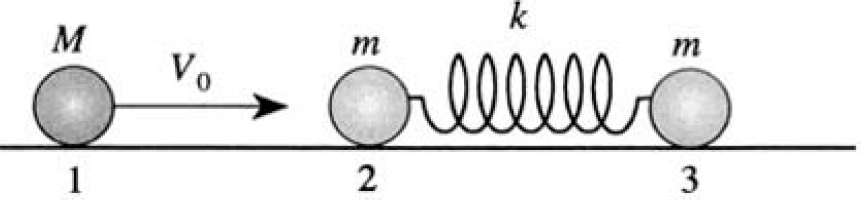
Figure 1.2a
conservation:
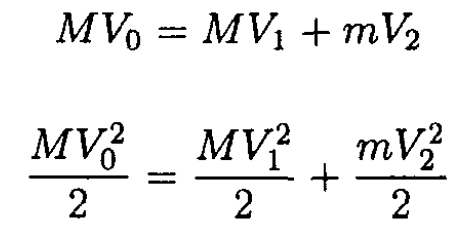
Again,
 (1)
(1)
 (2)
(2)

After the collision the first ball will move with constant velocity V1 and so its position coordinate x1 = V1t = V0t(1- γ)/(1+ γ). The center of mass of balls 2 and 3 will also move with constant velocity Vc = V2/2 (since m2 = m3 = m) Therefore from (2)
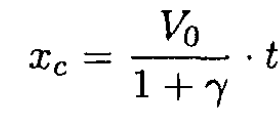
Now, in the center of mass frame of balls 2 and 3, the two balls are moving toward one another each with speed V2/2 and they will start to oscillate relative to the center of mass with the following time dependence:
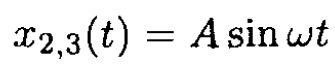
where  and k' is the spring constant of half of the spring, k' ≡ 2k. From energy conservation, the initial energy of mass 2 in the center of mass frame goes into the energy of spring deformation with an amplitude corresponding to the velocity change from V2/2 to zero:
and k' is the spring constant of half of the spring, k' ≡ 2k. From energy conservation, the initial energy of mass 2 in the center of mass frame goes into the energy of spring deformation with an amplitude corresponding to the velocity change from V2/2 to zero:
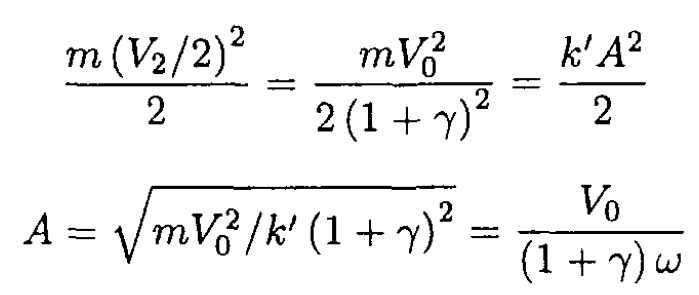
In the lab frame
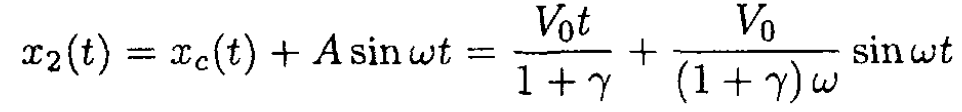
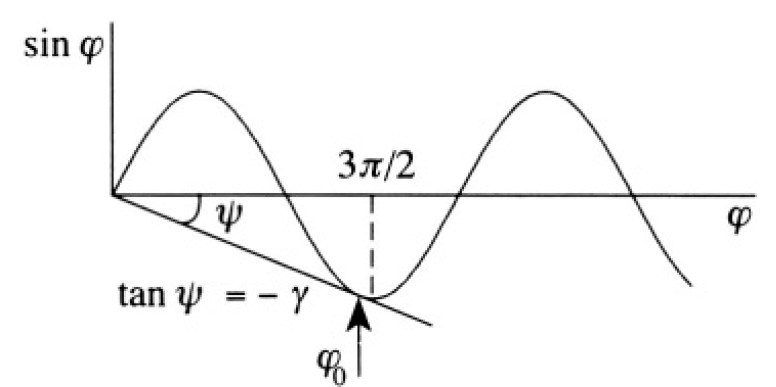
Figure 1.2b
For the second collision to occur, we need x1 = x2 or
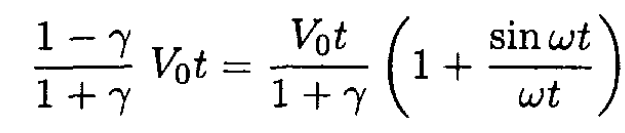 (3)
(3)
So we have
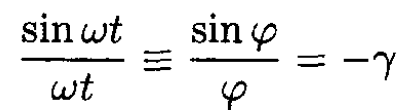 (4)
(4)
The easiest way is to solve (4) graphically (see Figure 1.2b). For the solution to exist, we have the condition γ ≤ γmax, where
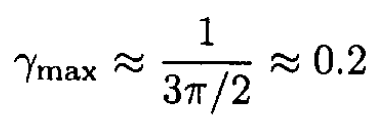
at φ0 ≈ 3π/2. The minimum value of the mass M = m/γmax ≈ 10 kg
b) The time between collisions is
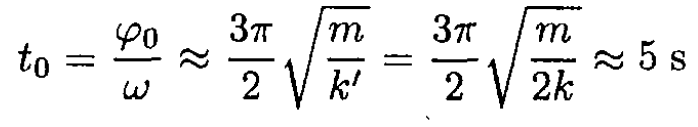
 الاكثر قراءة في مواضيع اخرى
الاكثر قراءة في مواضيع اخرى
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















