


 الفيزياء الكلاسيكية
الفيزياء الكلاسيكية
 الكهربائية والمغناطيسية
الكهربائية والمغناطيسية
 علم البصريات
علم البصريات
 الفيزياء الحديثة
الفيزياء الحديثة
 النظرية النسبية
النظرية النسبية
 الفيزياء النووية
الفيزياء النووية
 فيزياء الحالة الصلبة
فيزياء الحالة الصلبة
 الليزر
الليزر
 علم الفلك
علم الفلك
 المجموعة الشمسية
المجموعة الشمسية
 الطاقة البديلة
الطاقة البديلة
 الفيزياء والعلوم الأخرى
الفيزياء والعلوم الأخرى
 مواضيع عامة في الفيزياء
مواضيع عامة في الفيزياء|
Read More
Date: 22-8-2016
Date: 28-7-2016
Date: 9-8-2016
|
Rolling Coin
A coin idealized as a uniform disk of radius a with negligible thickness and mass m rolls in a circle. The center of mass of the coin C moves in a circle of radius b and the axis of the coin is tilted at an angle θ with respect to the vertical. Find the angular velocity Ω of the center of mass of the coin (see Figure 1.1).

Figure 1.1
SOLUTION
We can use the standard method of Euler equations to solve this problem. However, since the coin has a symmetry axis, it is easier to use a frame of reference rotating with angular velocity Ω, corresponding to the rotation of the center of mass of the coin. Rolling without slipping implies that the velocity of the point of contact with the table should be zero, and therefore
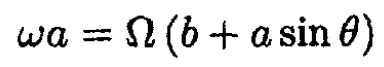 (1)
(1)
where ω is the angular velocity of rotation of the coin around its axis (see Figure 1.2). We have in this frame
 (2)
(2)
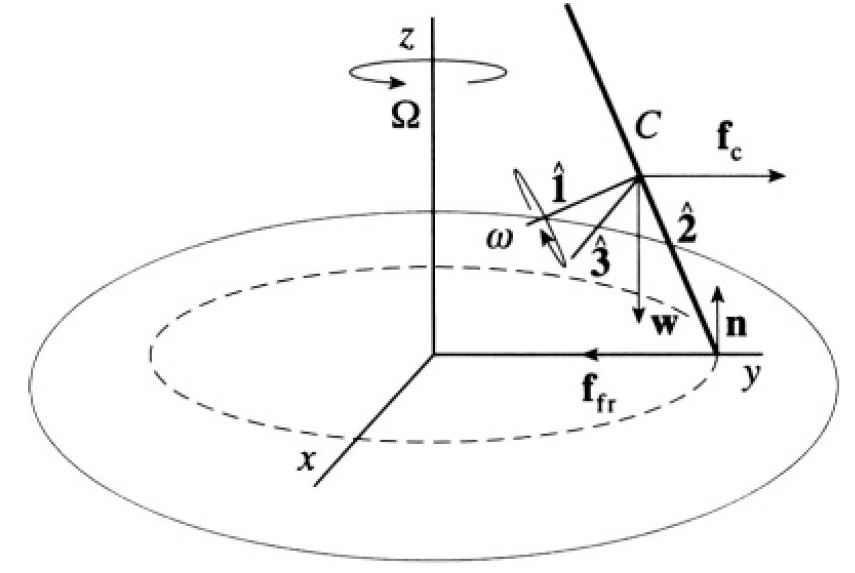
Figure 1.2
where n is the normal reaction, and w is the weight. From (2), we can find the torque N relative to the center of mass of the coin:
 (3)
(3)
In a non-inertial frame rotating with an angular velocity Ω, we can write
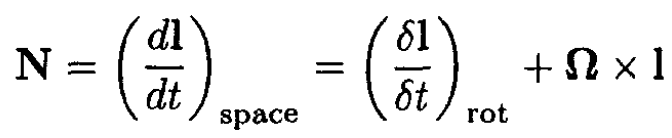 (4)
(4)
In the rotating frame
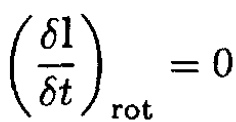
Choose the moment of time when one axis is horizontal and in the same direction as  (
(  in Figure 1.2). Since the axis of this frame coincides with the principal axis, the tensor of inertia is diagonal
in Figure 1.2). Since the axis of this frame coincides with the principal axis, the tensor of inertia is diagonal
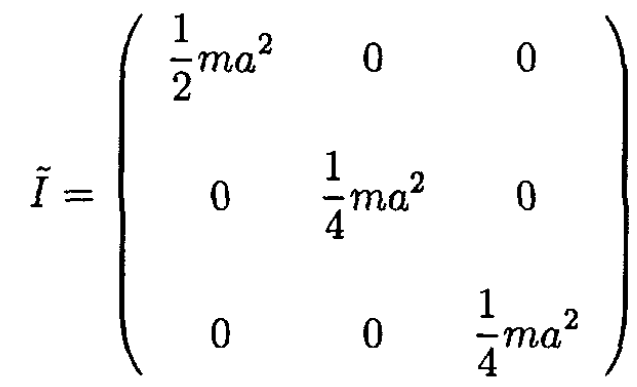
To calculate this tensor, we used I1 = (1/2)ma2 for the moment of inertia of the disk about its symmetry axis and also the fact that for a body of negligible thickness I1= I2 + I3. On the other hand  where
where
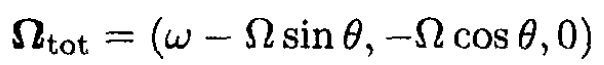
Taking N from (4) we have
 (5)
(5)
From (1)
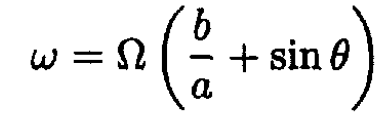 (6)
(6)
Comparing (5) with (3) and using (6) we obtain
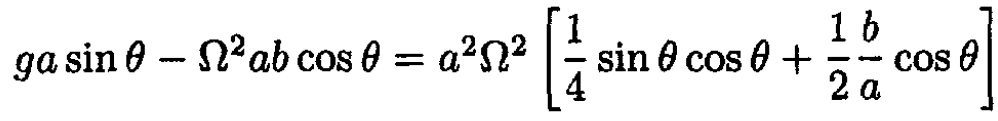 (7)
(7)
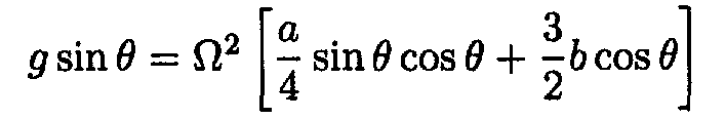 (8)
(8)
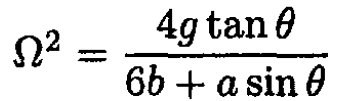 (9)
(9)



|
|
|
|
دراسة: حفنة من الجوز يوميا تحميك من سرطان القولون
|
|
|
|
|
|
|
تنشيط أول مفاعل ملح منصهر يستعمل الثوريوم في العالم.. سباق "الأرنب والسلحفاة"
|
|
|
|
|
|
|
لتعزيز التواصل مع الزائرات الأجنبيات : العتبة العلويّة المقدّسة تُطلق دورة لتعليم اللغة الإنجليزية لخادمات القسم النسويّ
|
|
|