


 الفيزياء الكلاسيكية
الفيزياء الكلاسيكية
 الكهربائية والمغناطيسية
الكهربائية والمغناطيسية
 علم البصريات
علم البصريات
 الفيزياء الحديثة
الفيزياء الحديثة
 النظرية النسبية
النظرية النسبية
 الفيزياء النووية
الفيزياء النووية
 فيزياء الحالة الصلبة
فيزياء الحالة الصلبة
 الليزر
الليزر
 علم الفلك
علم الفلك
 المجموعة الشمسية
المجموعة الشمسية
 الطاقة البديلة
الطاقة البديلة
 الفيزياء والعلوم الأخرى
الفيزياء والعلوم الأخرى
 مواضيع عامة في الفيزياء
مواضيع عامة في الفيزياء|
Read More
Date: 2-8-2016
Date: 26-8-2016
Date: 7-8-2016
|
Rotating Door
A uniform rectangular door of mass m with sides a and b (b > a) and negligible thickness rotates with constant angular velocity ω about a diagonal (see Figure 1.1). Ignore gravity. Show that the torque |N| = [m(b2 – a2)abω2]/[12(a2 + b2)] must be applied to keep the axis of rotation fixed.

Figure 1.1
SOLUTION
We will use the frame rotating with the door (body frame, axes 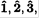 see Figure 1.2), so that we can use the Euler equations
see Figure 1.2), so that we can use the Euler equations
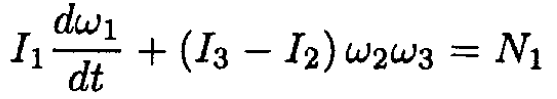 (1)
(1)
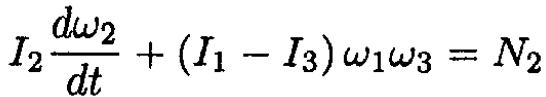 (2)
(2)
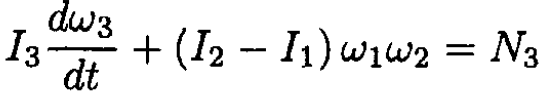 (3)
(3)
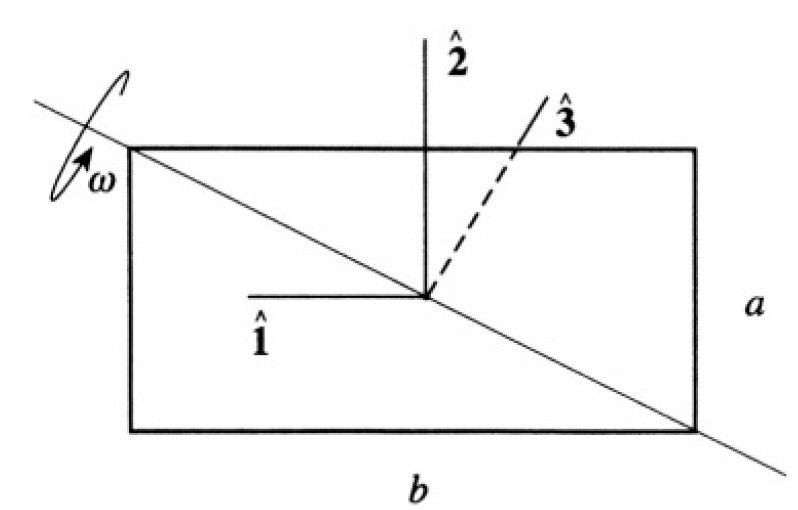
Figure 1.2
Where ω1, ω2, ω3 are the components of angular velocity in this frame and I1, I2, I3 are the principal moments of inertia. In this case I1 and I2 correspond to the moments of inertia of rods of length a and b respectively, which can be calculated easily:

Since the problem is two-dimensional (we can disregard the thickness of the door),
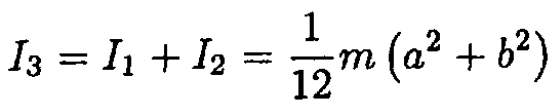
In our frame ω3 = 0 and ω1 and ω2 are constant.
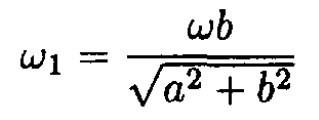 (4)
(4)
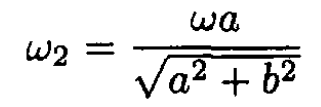 (5)
(5)
Substituting (4) and (5) into (1)–(3) we obtain
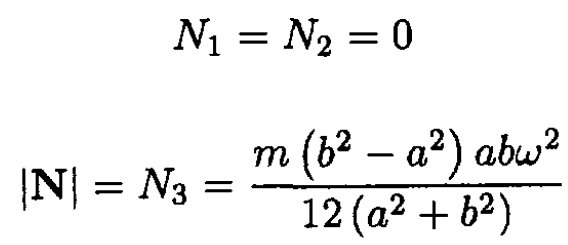



|
|
|
|
لصحة القلب والأمعاء.. 8 أطعمة لا غنى عنها
|
|
|
|
|
|
|
حل سحري لخلايا البيروفسكايت الشمسية.. يرفع كفاءتها إلى 26%
|
|
|
|
|
|
|
جامعة الكفيل تحتفي بذكرى ولادة الإمام محمد الجواد (عليه السلام)
|
|
|