
تاريخ الفيزياء

علماء الفيزياء


الفيزياء الكلاسيكية

الميكانيك

الديناميكا الحرارية


الكهربائية والمغناطيسية

الكهربائية

المغناطيسية

الكهرومغناطيسية


علم البصريات

تاريخ علم البصريات

الضوء

مواضيع عامة في علم البصريات

الصوت


الفيزياء الحديثة


النظرية النسبية

النظرية النسبية الخاصة

النظرية النسبية العامة

مواضيع عامة في النظرية النسبية

ميكانيكا الكم

الفيزياء الذرية

الفيزياء الجزيئية


الفيزياء النووية

مواضيع عامة في الفيزياء النووية

النشاط الاشعاعي


فيزياء الحالة الصلبة

الموصلات

أشباه الموصلات

العوازل

مواضيع عامة في الفيزياء الصلبة

فيزياء الجوامد


الليزر

أنواع الليزر

بعض تطبيقات الليزر

مواضيع عامة في الليزر


علم الفلك

تاريخ وعلماء علم الفلك

الثقوب السوداء


المجموعة الشمسية

الشمس

كوكب عطارد

كوكب الزهرة

كوكب الأرض

كوكب المريخ

كوكب المشتري

كوكب زحل

كوكب أورانوس

كوكب نبتون

كوكب بلوتو

القمر

كواكب ومواضيع اخرى

مواضيع عامة في علم الفلك

النجوم

البلازما

الألكترونيات

خواص المادة


الطاقة البديلة

الطاقة الشمسية

مواضيع عامة في الطاقة البديلة

المد والجزر

فيزياء الجسيمات


الفيزياء والعلوم الأخرى

الفيزياء الكيميائية

الفيزياء الرياضية

الفيزياء الحيوية

الفيزياء العامة


مواضيع عامة في الفيزياء

تجارب فيزيائية

مصطلحات وتعاريف فيزيائية

وحدات القياس الفيزيائية

طرائف الفيزياء

مواضيع اخرى
Thru-Earth Train
المؤلف:
Sidney B. Cahn Boris E. Nadgorny
المصدر:
A GUIDE TO PHYSICS PROBLEMS
الجزء والصفحة:
part 1 , p 8
2-8-2016
2204
Thru-Earth Train
A straight tunnel is dug from New York to San Francisco, a distance of 5000 kilometers measured along the surface. A car rolling on steel rails is released from rest at New York, and rolls through the tunnel to San Francisco (see Figure 1.1).
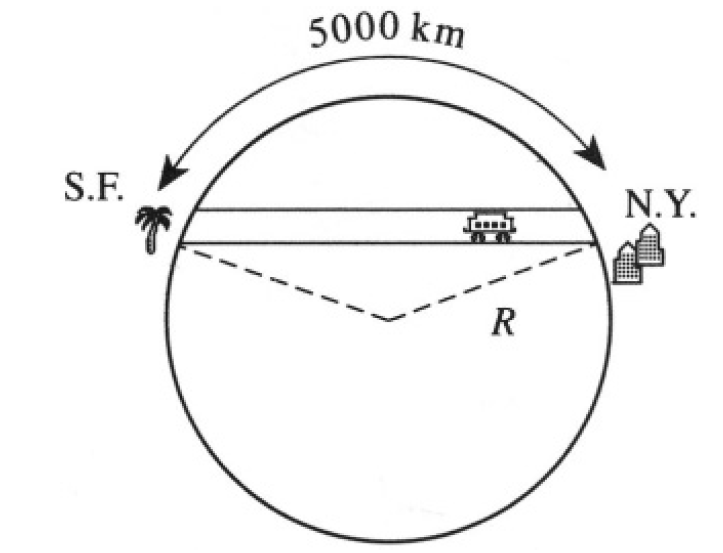
Figure 1.1
a) Neglecting friction and also the rotation of the Earth, how long does it take to get there? Take the gravitational acceleration g = 980 m/s2 and the radius of the Earth R = 6400 km.
b) Suppose there is now friction proportional to the square of the velocity (but still ignoring the rotation of the Earth). What is the equation for the phase space trajectory? Introduce suitable symbols for the constant of proportionality and for the mass of the car, and also draw a sketch.
c) We now consider the effects of rotation. Estimate the magnitude of the centrifugal and Coriolis forces relative to the gravitational force (ignore friction). Take New York and San Francisco to be of equal latitude (approximately 40° North).
SOLUTION
a) The radial force acting on a particle at any given point inside the Earth depends only on the mass of the sphere whose radius is at that point (see
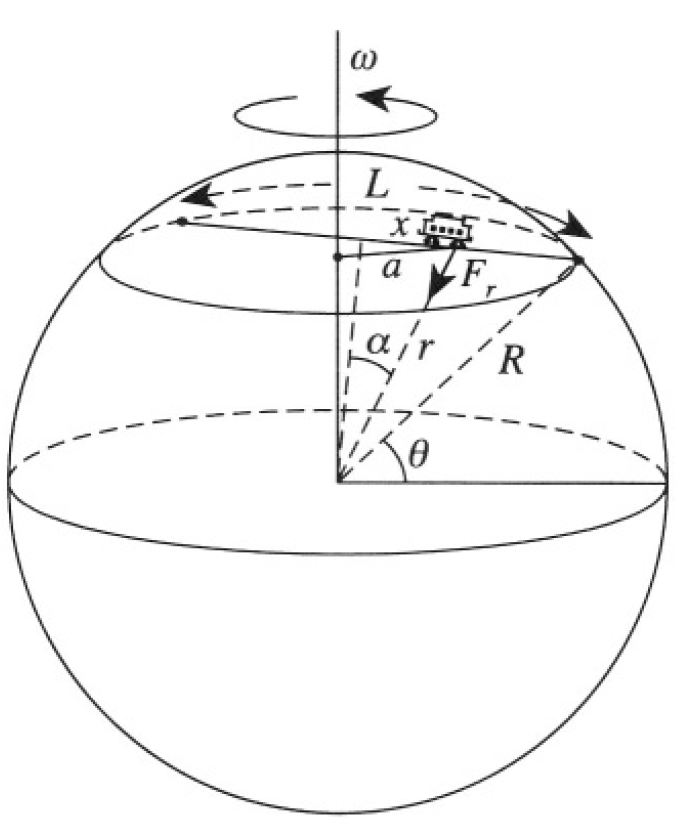
Figure 1.2a
Figure 1.2a):

where m is the mass of the car, so
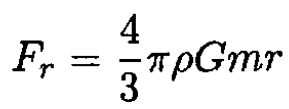
The accelerating force will be
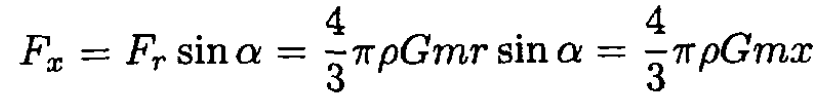
so we have
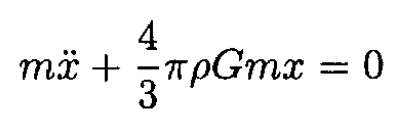
On the surface of the Earth
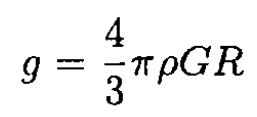
resulting in

which describes oscillatory motion of frequency  Half of the period of this oscillation is the time for the train to get to San Francisco
Half of the period of this oscillation is the time for the train to get to San Francisco
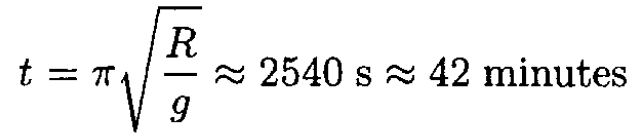
b) If there is friction proportional to the square of velocity we have an additional term

where α is the proportionality coefficient for the friction force. Using p = mẋ we obtain
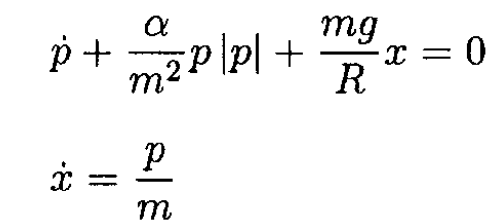
Or
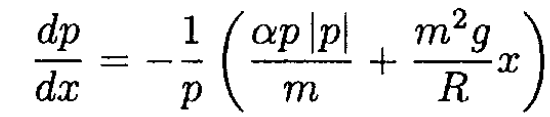
(see Figure 1.2b).
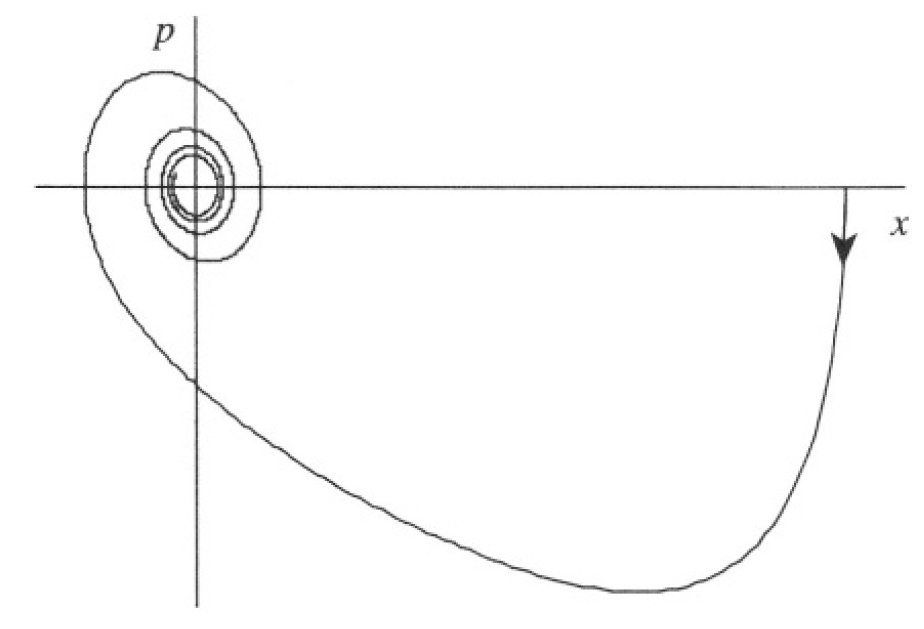
Figure 1.2b
c) The acceleration due to the centrifugal force is given by the formula
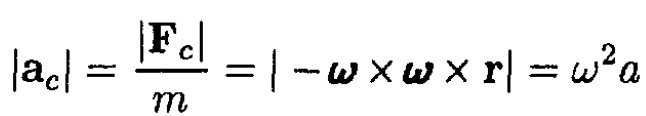
where is defined in Figure 1.2a, and ω = 2π/T is the angular frequency of the Earth’s rotation. So the maximum centrifugal acceleration |ac|max is on the surface of the Earth

For New York θ ≈ 40o yielding
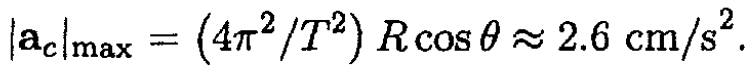
So the centrifugal force is only about 0.3% of the gravitational force. The acceleration due to the Coriolis force is
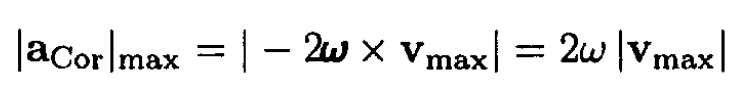
From (a):
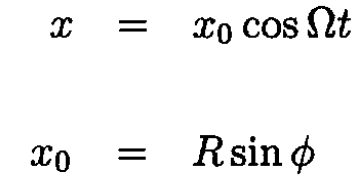
Where ϕ = L/2R = 2500/6400 ≈ 0.39 rad. So,
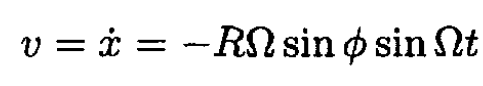
and |aCor|max = 2ωΩRsinϕ, where Ω is the frequency of oscillation found in (a): 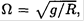 and so
and so 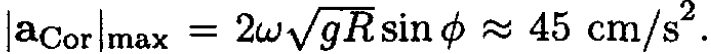 Hence, the Coriolis force is about 5% of the gravitational force.
Hence, the Coriolis force is about 5% of the gravitational force.
 الاكثر قراءة في مواضيع اخرى
الاكثر قراءة في مواضيع اخرى
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















