
تاريخ الفيزياء

علماء الفيزياء


الفيزياء الكلاسيكية

الميكانيك

الديناميكا الحرارية


الكهربائية والمغناطيسية

الكهربائية

المغناطيسية

الكهرومغناطيسية


علم البصريات

تاريخ علم البصريات

الضوء

مواضيع عامة في علم البصريات

الصوت


الفيزياء الحديثة


النظرية النسبية

النظرية النسبية الخاصة

النظرية النسبية العامة

مواضيع عامة في النظرية النسبية

ميكانيكا الكم

الفيزياء الذرية

الفيزياء الجزيئية


الفيزياء النووية

مواضيع عامة في الفيزياء النووية

النشاط الاشعاعي


فيزياء الحالة الصلبة

الموصلات

أشباه الموصلات

العوازل

مواضيع عامة في الفيزياء الصلبة

فيزياء الجوامد


الليزر

أنواع الليزر

بعض تطبيقات الليزر

مواضيع عامة في الليزر


علم الفلك

تاريخ وعلماء علم الفلك

الثقوب السوداء


المجموعة الشمسية

الشمس

كوكب عطارد

كوكب الزهرة

كوكب الأرض

كوكب المريخ

كوكب المشتري

كوكب زحل

كوكب أورانوس

كوكب نبتون

كوكب بلوتو

القمر

كواكب ومواضيع اخرى

مواضيع عامة في علم الفلك

النجوم

البلازما

الألكترونيات

خواص المادة


الطاقة البديلة

الطاقة الشمسية

مواضيع عامة في الطاقة البديلة

المد والجزر

فيزياء الجسيمات


الفيزياء والعلوم الأخرى

الفيزياء الكيميائية

الفيزياء الرياضية

الفيزياء الحيوية

الفيزياء العامة


مواضيع عامة في الفيزياء

تجارب فيزيائية

مصطلحات وتعاريف فيزيائية

وحدات القياس الفيزيائية

طرائف الفيزياء

مواضيع اخرى
Vibrating String with Mass
المؤلف:
Sidney B. Cahn Boris E. Nadgorny
المصدر:
A GUIDE TO PHYSICS PROBLEMS
الجزء والصفحة:
part 1 , p 27
2-8-2016
1462
Vibrating String with Mass
A thin uniform string of length L and linear density ρ is stretched between two firm supports. The tension in the string is T (see Figure 1.1).
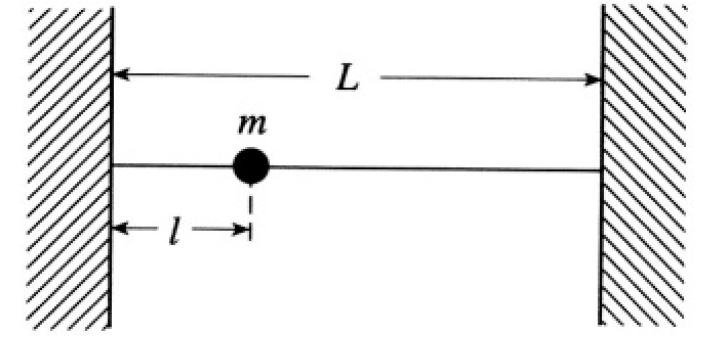
Figure 1.1
a) Derive from first principles the wave equation for small transverse disturbances in the string.
b) Determine the set of possible solutions for the given boundary conditions and state the allowed frequencies.
c) A small mass m is placed a distance l from one end of the string. Determine the first-order correction to the frequencies of the modes found in (b).
SOLUTION
a) To derive the equation of motion of the string we assume that the oscillations of the string are small, the tension T is a slowly varying function
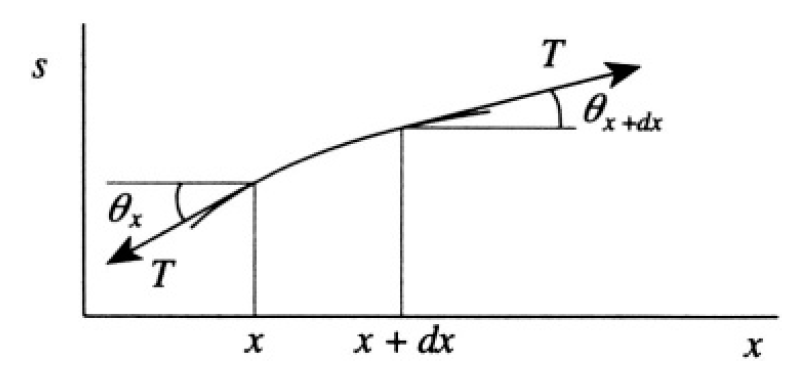
Figure 1.2
of x, and there is no damping of the motion. Consider a part of the string between x and x + dx, where s (x, t) is the transverse displacement of the string (see Figure 1.2). The transverse force acting on this piece of mass ρdx is
 (1)
(1)
Using the initial assumptions, we can substitute a constant T for the tension T(x) and write
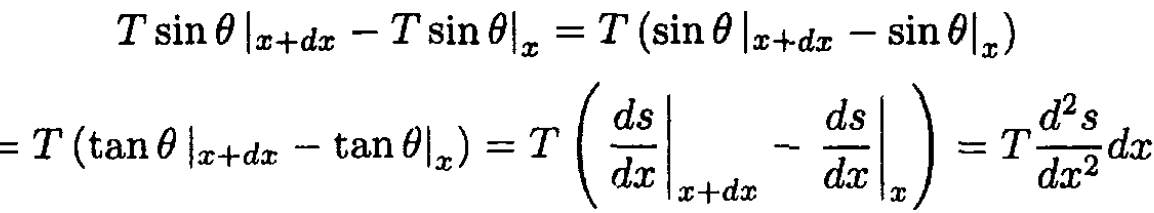 (2)
(2)
where the substitution of tan θ for sin θ again follows from assumptions. Using (2) in (1), we obtain
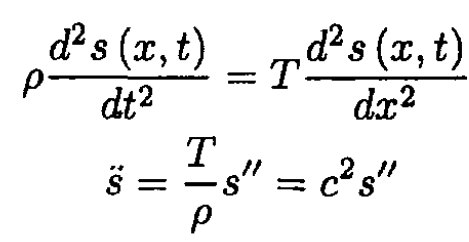 (3)
(3)
where  is the wave velocity.
is the wave velocity.
b) Now, we have boundary conditions. We choose a standing wave solution. Another possible solution is a traveling wave s (x, t) = f(x + ct) + g (x – ct), where f and g are some functions. In our case, we use the method of separation of variables: s (x, t) = g(x) f(t), which, substituted into (3), gives
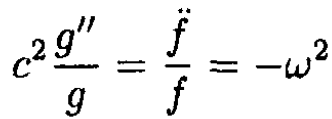
where ω2 is a constant independent of x and t. We arrive at two secondorder differential equations for f and g and their solutions:
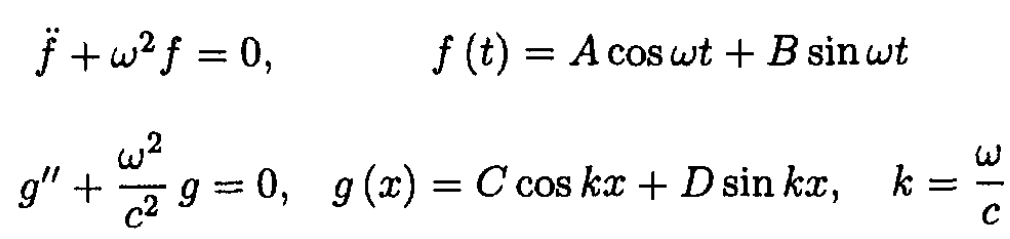
Applying the boundary condition to the solution:
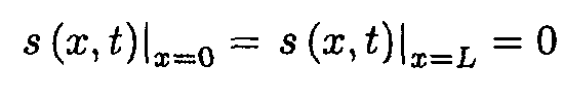
from which we get
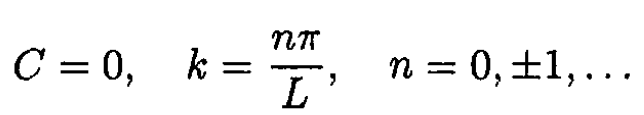
For each mode gn (x) = sin (ωn x/c) and fn (t) = An cos ωnt + Bn sin ωnt with ωn ≡ ncπ/L. For each complete mode
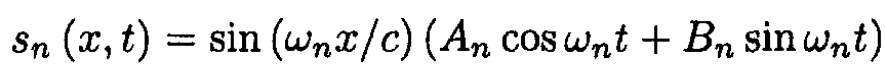
and the transverse displacement is
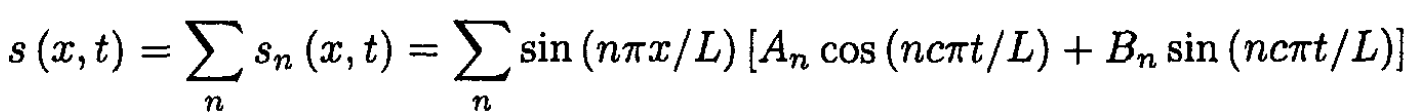
c) To find the frequency change, use a perturbation method. Consider for simplicity the nth mode of the form sn = sin(nπx/L) cos ωnt, corresponding to the initial conditions s (x, 0) = s0 (x) and  We know from the virial theorem that initially the average of potential energy of the string in the nth mode is equal to the kinetic energy:
We know from the virial theorem that initially the average of potential energy of the string in the nth mode is equal to the kinetic energy:
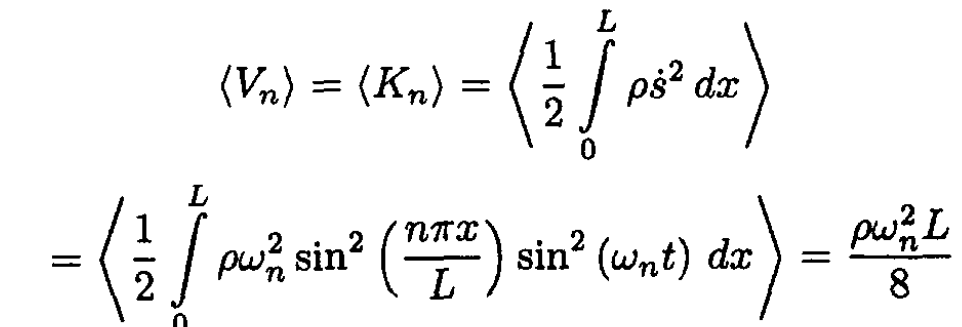 (4)
(4)
where we used  Now examine the mode of the string with mass to be of the same form as in (S.1.46.4): sn (x, t) = sin(nπx/L) cos Ωnt with a slightly different frequency Ωn. Find the kinetic energy
Now examine the mode of the string with mass to be of the same form as in (S.1.46.4): sn (x, t) = sin(nπx/L) cos Ωnt with a slightly different frequency Ωn. Find the kinetic energy 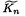 in this mode of the string and then add the kinetic energy of the additional mass:
in this mode of the string and then add the kinetic energy of the additional mass:
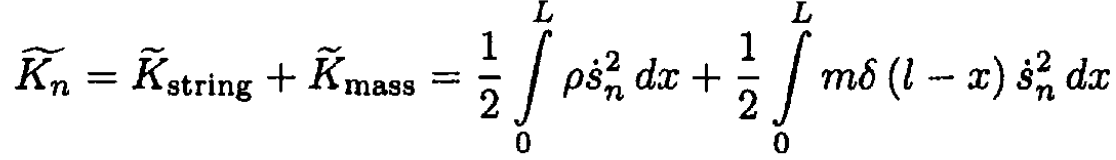
where δ (l – x) is the Dirac δ function. The average kinetic energy of the string with mass from (5)
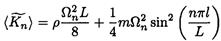 (6)
(6)
where again we used 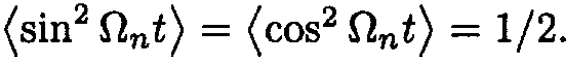 In this approximation, if we ignore the change in tension T, the average potential energy of the string with mass is the same as for the string alone, so
In this approximation, if we ignore the change in tension T, the average potential energy of the string with mass is the same as for the string alone, so 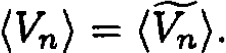 Utilizing this together with the virial theorem, which is also true for the modified string, we may write
Utilizing this together with the virial theorem, which is also true for the modified string, we may write
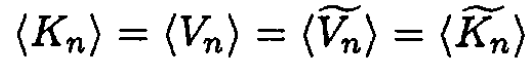 (7)
(7)
So from (5)–( 7)
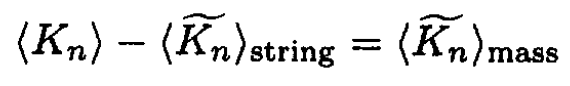
or
 (8)
(8)
Therefore the new frequency
 (9)
(9)
where we used m << ρL.
 الاكثر قراءة في مواضيع اخرى
الاكثر قراءة في مواضيع اخرى
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















