
تاريخ الفيزياء

علماء الفيزياء


الفيزياء الكلاسيكية

الميكانيك

الديناميكا الحرارية


الكهربائية والمغناطيسية

الكهربائية

المغناطيسية

الكهرومغناطيسية


علم البصريات

تاريخ علم البصريات

الضوء

مواضيع عامة في علم البصريات

الصوت


الفيزياء الحديثة


النظرية النسبية

النظرية النسبية الخاصة

النظرية النسبية العامة

مواضيع عامة في النظرية النسبية

ميكانيكا الكم

الفيزياء الذرية

الفيزياء الجزيئية


الفيزياء النووية

مواضيع عامة في الفيزياء النووية

النشاط الاشعاعي


فيزياء الحالة الصلبة

الموصلات

أشباه الموصلات

العوازل

مواضيع عامة في الفيزياء الصلبة

فيزياء الجوامد


الليزر

أنواع الليزر

بعض تطبيقات الليزر

مواضيع عامة في الليزر


علم الفلك

تاريخ وعلماء علم الفلك

الثقوب السوداء


المجموعة الشمسية

الشمس

كوكب عطارد

كوكب الزهرة

كوكب الأرض

كوكب المريخ

كوكب المشتري

كوكب زحل

كوكب أورانوس

كوكب نبتون

كوكب بلوتو

القمر

كواكب ومواضيع اخرى

مواضيع عامة في علم الفلك

النجوم

البلازما

الألكترونيات

خواص المادة


الطاقة البديلة

الطاقة الشمسية

مواضيع عامة في الطاقة البديلة

المد والجزر

فيزياء الجسيمات


الفيزياء والعلوم الأخرى

الفيزياء الكيميائية

الفيزياء الرياضية

الفيزياء الحيوية

الفيزياء العامة


مواضيع عامة في الفيزياء

تجارب فيزيائية

مصطلحات وتعاريف فيزيائية

وحدات القياس الفيزيائية

طرائف الفيزياء

مواضيع اخرى
Betatron
المؤلف:
Sidney B. Cahn Boris E. Nadgorny
المصدر:
A GUIDE TO PHYSICS PROBLEMS
الجزء والصفحة:
part 1 , p 75
7-8-2016
2174
Betatron
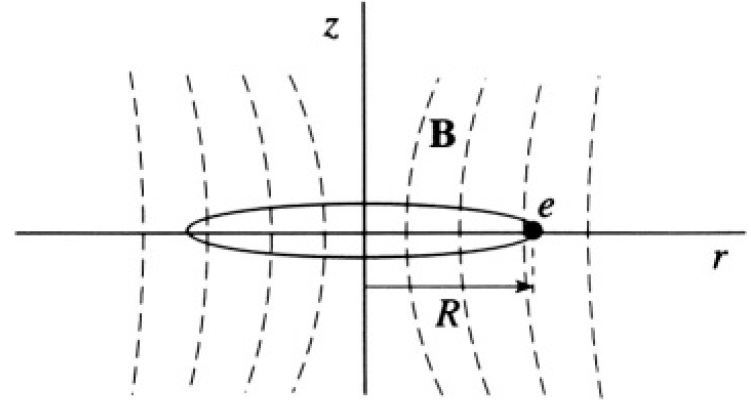
Consider the motion of electrons in an axially symmetric magnetic field. Suppose that at z = 0 (the “median plane”) the radial component of the
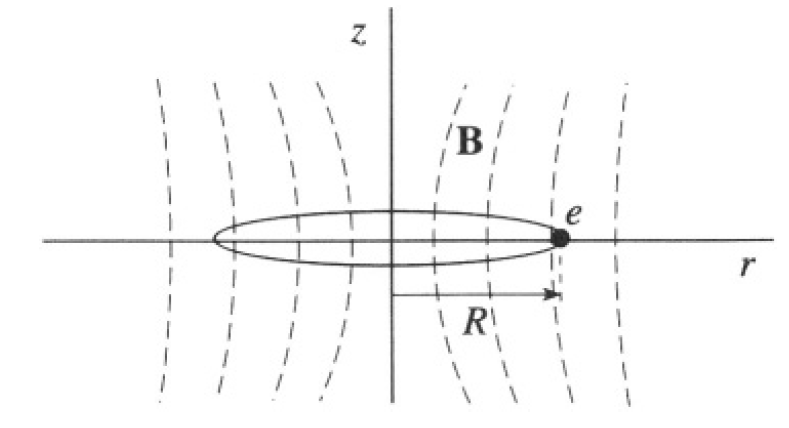
Figure 1.1
magnetic field is 0, so B(z = 0) = B (r)ẑ. Electrons at z = 0 then follow a circular path of radius R (see Figure 1.1).
a) What is the relationship between the electron momentum p and the orbit radius R?
In a betatron, electrons are accelerated by a magnetic field which changes with time. Let (B) equal the average value of the magnetic field over the plane of the orbit (within the orbit), i.e.,

where Φ is the magnetic flux through the orbit. Let B0 equal B(r = R, z = 0).
b) Suppose (B) is changed by an amount (ΔB) and B0 is changed by ΔB0. How must (ΔB) be related to ΔB0 if the electrons are to remain at radius R as their momentum is increased?
c) Suppose the z component of the magnetic field near r = R and z = 0 varies with r as Bz (r) = B0(R) (R/r)n. Find the equations of motion for small departures from the equilibrium orbit in the median plane. There are two equations, one for small vertical changes and one for small radial changes. Neglect any coupling between radial and vertical motion.
d) For what range of n is the orbit stable against both vertical and radial perturbations?
SOLUTION
a) Assume we have a magnetic field that is constant along and perpendicular to the plane of the orbit B (z = 0) = B(R) ẑ. The Lorentz force gives
 (1)
(1)
We can substitute the energy ε for the momentum by using

and since the energy does not change in the magnetic field we have
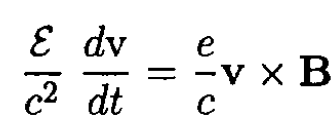 (2)
(2)
or, separating into components,
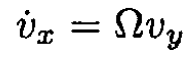 (3)
(3)
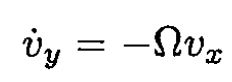 (4)
(4)
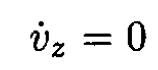
where
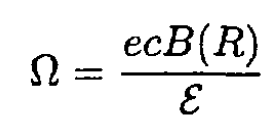 (5)
(5)
Following a standard procedure, we multiply (4) by  and add it to (3), which yields
and add it to (3), which yields
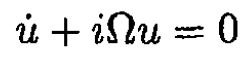 (6)
(6)
where u = vx + ivy or
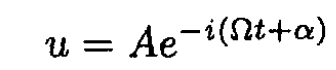 (7)
(7)
where A and α are real. Separating real and imaginary parts of (7), we obtain
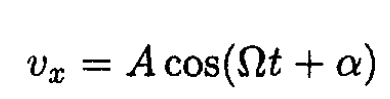 (8)
(8)
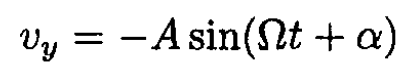 (9)
(9)
From (8) and (9), we can see that
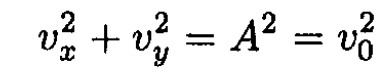
where v0 is the initial velocity of the particle, which as we assumed moves only in the x – y plane. Integrating again, we find
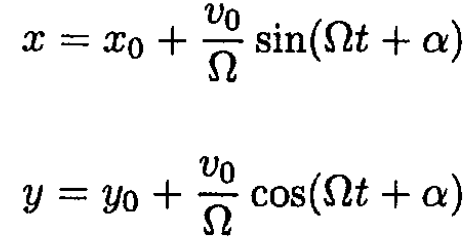 (10)
(10)
So the radius R is given by
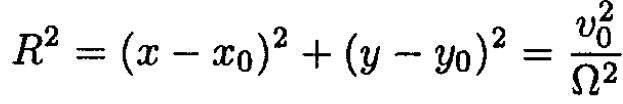 (11)
(11)
and
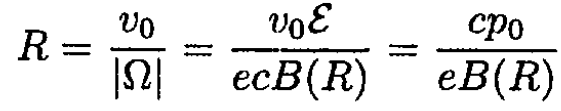 (12)
(12)
b) From (12), the momentum
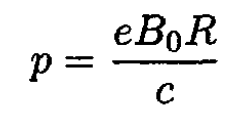 (13)
(13)
where B0 =B0 (R). Assuming that R does not change, we find from (13) that
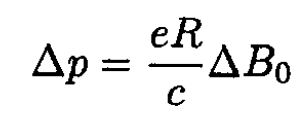 (14)
(14)
If the magnetic field through the orbit is increased, a tangential electric field will be produced at the position of the orbit:
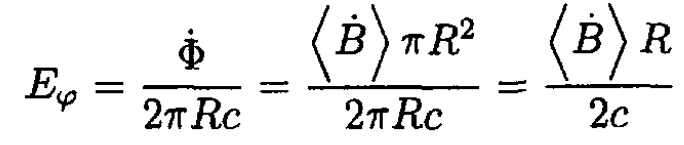 (15)
(15)
Therefore the rate of increase of the momentum is
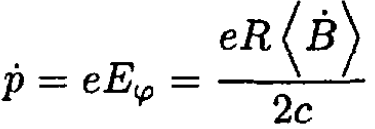 (16)
(16)
Integrating (16), we obtain
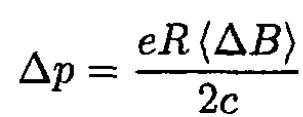 (17)
(17)
Equating (14) and (17), we have
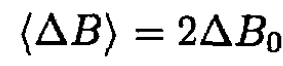 (18)
(18)
indicating that the change in flux through the orbit must be twice that which would have been obtained if the magnetic field were spatially uniform (Betatron rule 2:1).
c) Consider first the vertical displacement (we assume that the vertical and radial motions are decoupled)
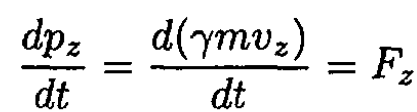 (19)
(19)
where 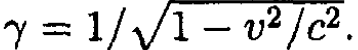 Since vz is much smaller than the velocity in the x–y plane, we disregard any change in γ due to changes in vz
Since vz is much smaller than the velocity in the x–y plane, we disregard any change in γ due to changes in vz
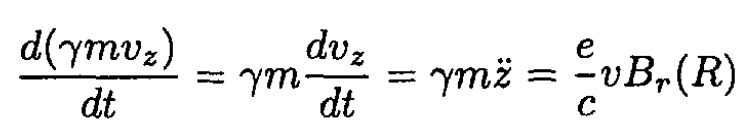 (20)
(20)
where Br (R) is the radial B field at a radius R. Neglecting the space charge current and displacement current and using cylindrical coordinates, we may write
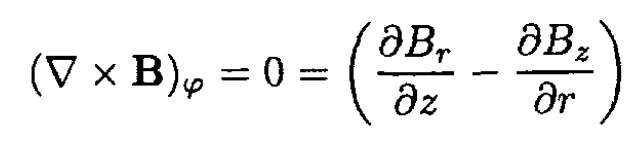
So
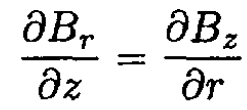
or, for small z,
 (21)
(21)
Using the expression for Bz given in the problem,
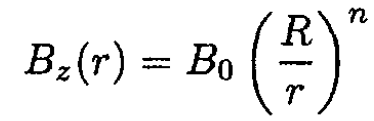
and substituting it into (21) and then (20), we obtain
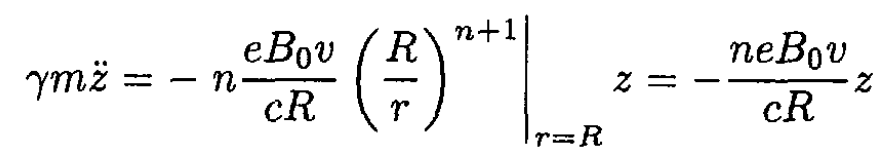 (22)
(22)
So
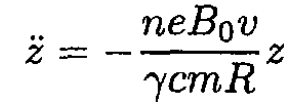 (23)
(23)
Taking v = ΩR from (12), (23) becomes
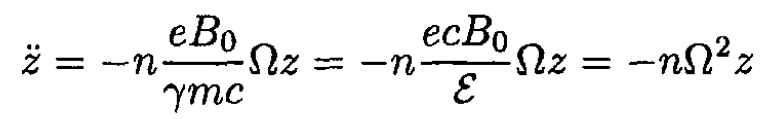 (24)
(24)
Therefore (24) exhibits oscillatory behavior along the z-axis which is stable if nΩ2 > 0 and so n > 0. The period of oscillation is then
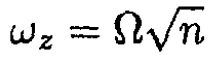 (25)
(25)
For the radial motion, the Lorentz force FL is
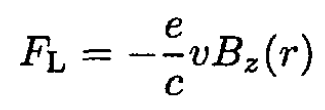 (26)
(26)
For small deviations from equilibrium ρ ≡ r – R, we can write (26) in the form
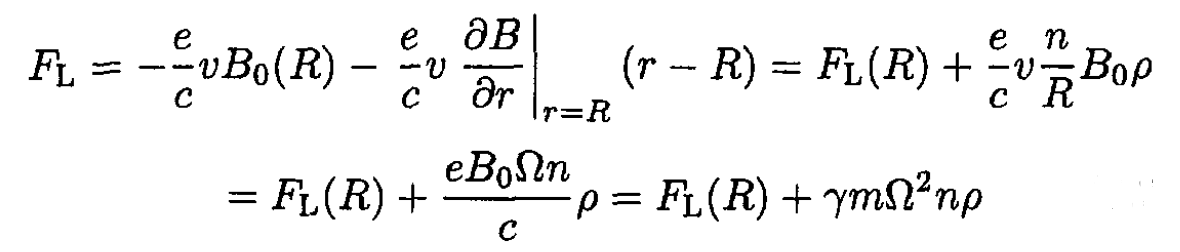 (27)
(27)
where we again used (12) for the cyclotron frequency. We must also consider the centrifugal force
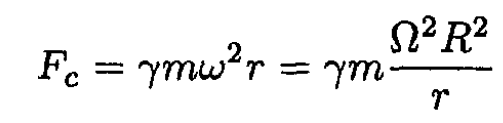 (28)
(28)
where we used the conservation of canonical angular momentum
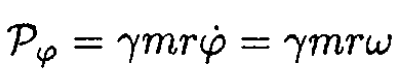
Now, for small ρ,
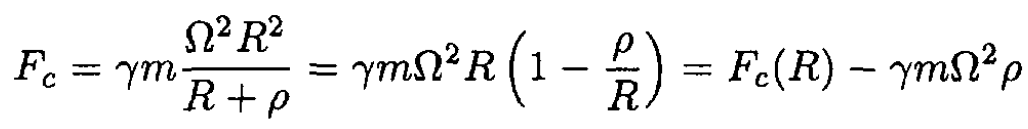 (29)
(29)
Combining (27) and (29), we obtain
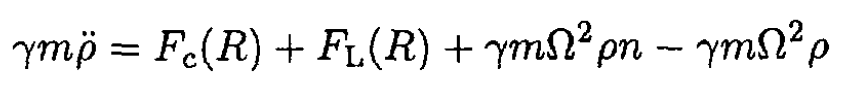 (30)
(30)
Since Fc (R) + FL (R) = 0 at equilibrium, we can write
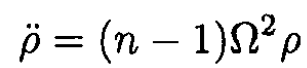 (31)
(31)
Again, as for the vertical motion, we have an oscillation of frequency
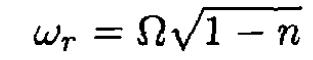
This oscillation is stable if 1 – n > 0, or n < 1.
d) The condition for both radial and vertical stability will be the intersection of the two conditions for n, so
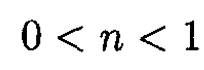
 الاكثر قراءة في مواضيع اخرى
الاكثر قراءة في مواضيع اخرى
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















