
Classical Atomic Spectral Line
 المؤلف:
Sidney B. Cahn Boris E. Nadgorny
المؤلف:
Sidney B. Cahn Boris E. Nadgorny
 المصدر:
A GUIDE TO PHYSICS PROBLEMS
المصدر:
A GUIDE TO PHYSICS PROBLEMS
 الجزء والصفحة:
part 1 , p 68
الجزء والصفحة:
part 1 , p 68
 8-8-2016
8-8-2016
 1833
1833
Classical Atomic Spectral Line
Consider the classical theory of the width of an atomic spectral line. The “atom” consists of an electron of mass m and charge in a harmonic oscillator potential. There is also a frictional damping force, so the equation of motion for the electron is
 (1)
(1)
a) Suppose at time t = 0, x = x0 and ẋ = 0. What is the subsequent motion of the electron? A classical electron executing this motion would emit electromagnetic radiation. Determine the intensity I(ω) of this radiation as a function of frequency. (You need not calculate the absolute normalization of I(ω), only the form of the ω dependence of I(ω). In other words, it is enough to calculate up to a constant of proportionality.) Assume γ/m << ω0.
b) Now suppose the damping force γẋ is absent from (1) and that the oscillation is damped only by the loss of energy to radiation (an effect which has been ignored above). The energy U of the oscillator decays as U0e-Γt. What, under the above assumptions, is Γ. (You may assume that in any one oscillation the electron loses only a very small fraction of its energy.)
c) For an atomic spectral line of 5000 Å, what is the width of the spectral line, in angstroms, as determined from the calculation of (b)? About how many oscillations does the electron make while losing half its energy? Rough estimates are enough.
SOLUTION
a) The equation

has a solution
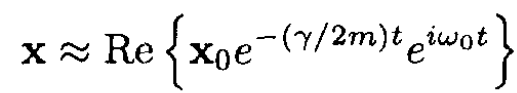 (1)
(1)
with initial conditions x = x0, and ẋ = 0, where we used
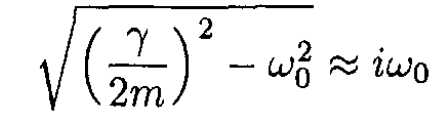
for ω0 >> γ/m. In the same approximation, the acceleration
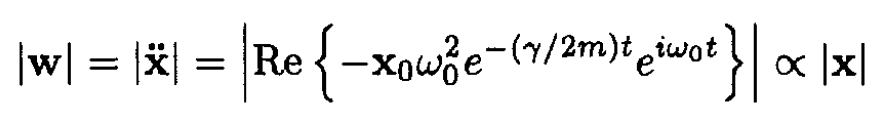 (2)
(2)
The total energy ε radiated by the atom
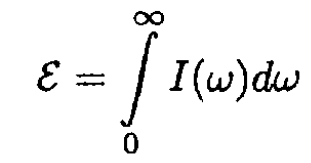 (3)
(3)
where I(ω) is the spectral density of the radiation. On the other hand
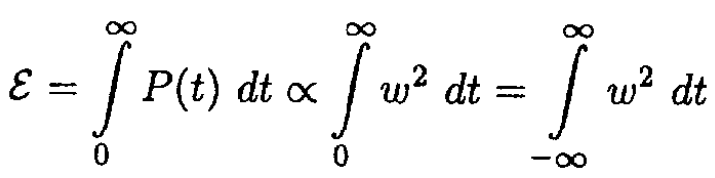 (4)
(4)
where we used the formula
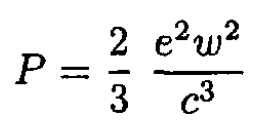 (5)
(5)
and the fact that w = 0 at t < 0. We may write the Fourier transform of the acceleration w:

Now, Parseval’s relation gives
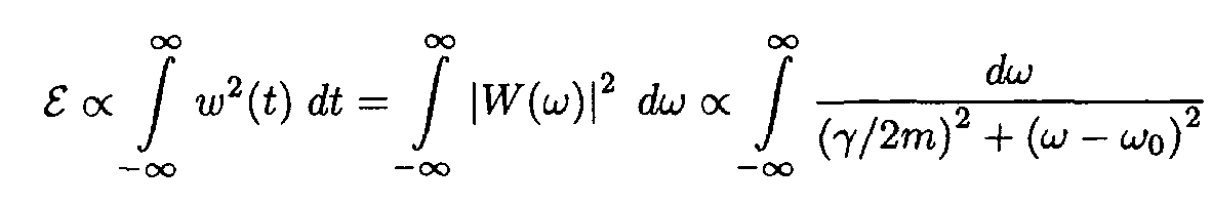 (6)
(6)
Comparing (3) and (6), we obtain for the spectral density
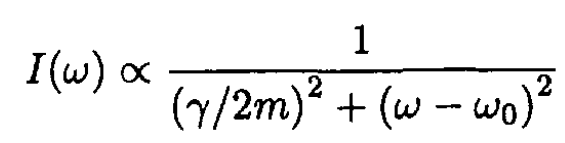
b) The energy U of the oscillator may be written
 (7)
(7)
The power loss is therefore
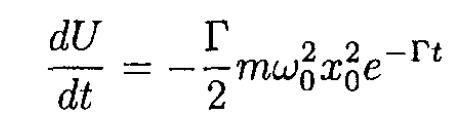 (8)
(8)
This may be equated to the power loss given by the average over one cycle of (5)
 (9)
(9)
c) We may rewrite (9) as
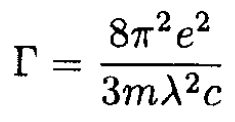
The linewidth in angstroms may be found from
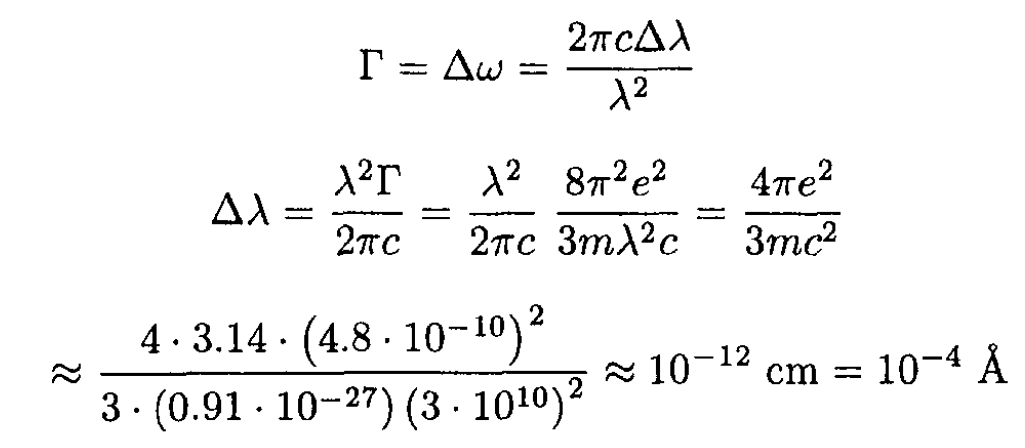
Now find the time T for the atom to lose half its energy:

The number of oscillations is then
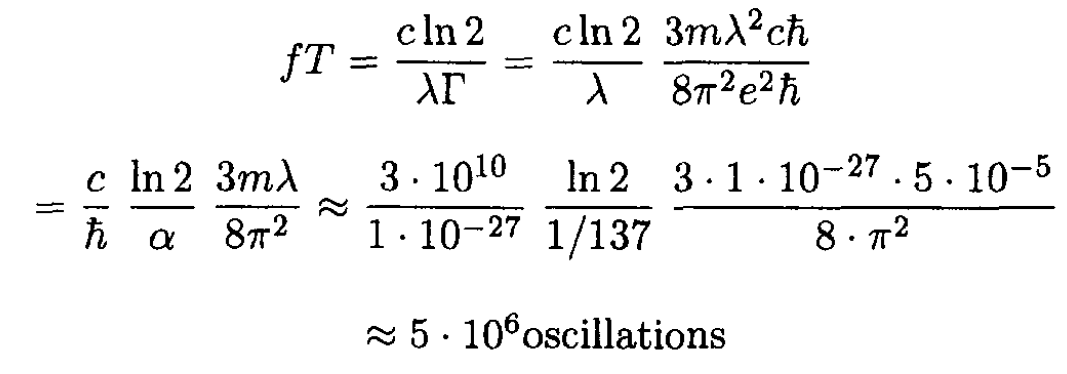
 الاكثر قراءة في مواضيع اخرى
الاكثر قراءة في مواضيع اخرى
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


