Electron and Radiation Reaction

The equation of motion for a particle of mass m and charge q in electric and magnetic fields E and B, including the radiation reaction force, is

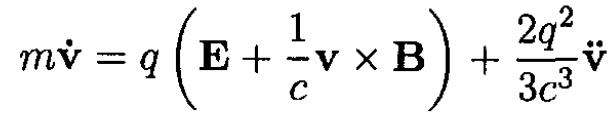
a) Assuming that the radiative reaction term is very small compared to the Lorentz force and that v << c, find an approximate expression for the radiative reaction force in terms of E and B.

b) A plane electromagnetic wave propagates in the z direction. A free electron is initially at rest in this wave. Under the assumptions of (a), calculate the time-averaged radiative reaction force on the electron (magnitude and direction). What result would you obtain for a positron?

c) Rederive the reaction force by considering the momentum acquired by the electron in the process of forced emission of radiation. Use the Thomson cross section σ

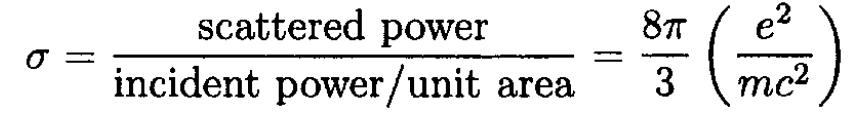
SOLUTION

a) By assuming that v << c, we may write

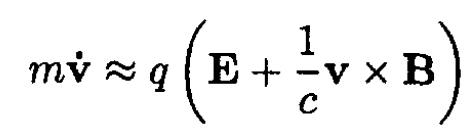(1)

Differentiating (1) with respect to time, we obtain

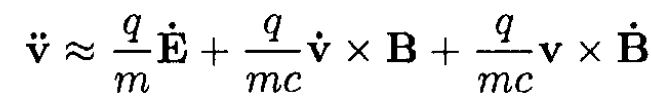(2)

Substituting for 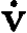 in (2) results in

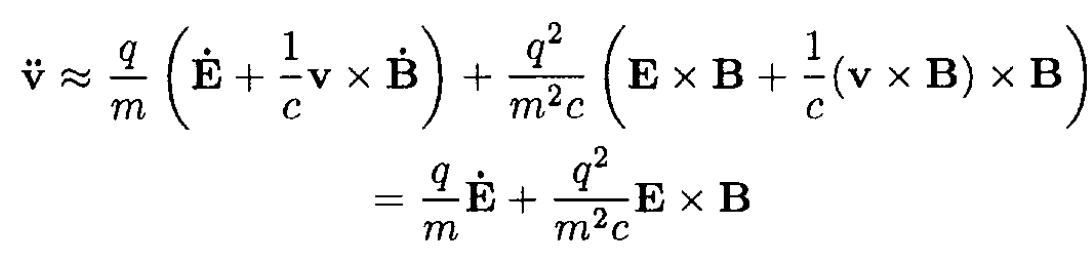
where we have disregarded terms first order in v/c. So

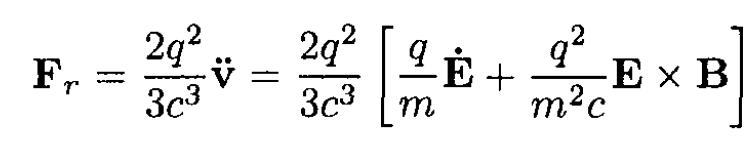(3)

b) Let the E field of the plane wave be polarized in the x direction, so that

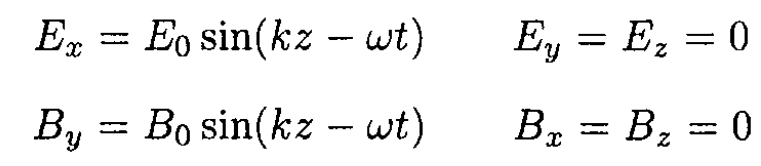
The time averages of (3) are

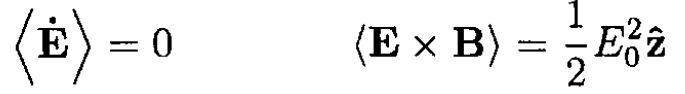
so that

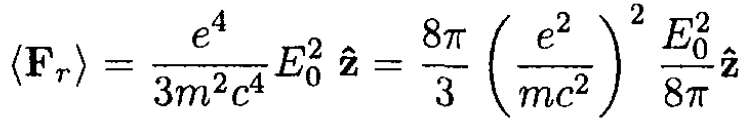(4)

The radiation reaction force varies with the fourth power of the charge, so a positron would yield the same result.

c) The average power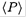 scattered by the charge is

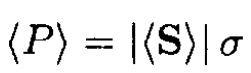(5)

where σ is the total cross section. The average power is then

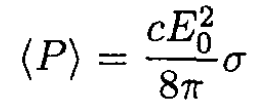(6)

The average incident momentum per unit time p_i is given by

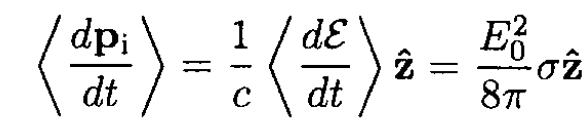(7)

where we used the relation ε = pc for radiation. Using the Thomson cross section for σ in (7) gives the reaction force

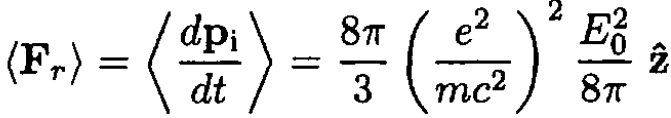
This is the same result as in (4).

اخر الاخبار

اخبار العتبة العباسية المقدسة

جولة تفقدية لمتابعة خطة تنظيم مداخل المعزّين المشاركين في عزاء ركضة طويريج

لتعزيز التعاون الأكاديمي والبحثي.. جامعة الكفيل توقع اتفاقيتي توأمة مع جامعتين عراقيتين

المجمَع العلميّ يواصل إقامة مجلسه العزائي بذكرى شهادة الإمام الحسين (عليه السلام) في النجف الأشرف

قسم حفظ النظام يواصل تنفيذ خطته لتنظيم سير المواكب والزائرين في شهر المحرم

المزيد

الآخبار الصحية

لهذا السبب.. إغلاق 25 مركزًا لعلاج الإدمان في مصر ؟

خلافا للاعتقاد الشائع.. علماء يكشفون أسرار بذور البطيخ ؟!

هذا ما يحدث لجسمك عند تناولك الطماطم بانتظام !

تعرف على أطعمة تسرّع "تعافي الجسم" من حروق الشمس

المزيد

الآخبار التكنلوجية

الثلوج تغطي الصحراء الأكثر جفافا في العالم!

بتلسكوب "ألما".. التقاط صورا غير مسبوقة لبدايات الكون !

هل هاتفك مراقب؟.. 5 علامات خطيرة تكشف التجسس عليك

دبي تطلق أول رحلة تجريبية للتاكسي الجوي

المزيد

مواضيع ذات صلة

جسيمات التماثل الفائق الفوتينوات ، سكواركات ..المادة الظل.. الأكسيونات ..إلخ .

ريادةالانسان للفضاء -قدرة الله في خلق الطيور(كيف الهمت الطيور الانسان )

التجريبية المنطقية وميكانيكا الكم: رؤية كاسيرر بين العلم والفلسفة

المفاهيم الفيزيائية بين الدقة العلمية والتأويل الفلسفي

"توحيد العلوم عبر استبعاد الميتافيزيقا

إرنست ماخ: توحيد الفيزياء عبر الإدراكات الحسية واستبعاد الميتافيزيقا

"الفيزياء بين الكلاسيكية والكم: من حتمية الأشياء إلى نسبية القوانين"

قوانين البقاء في الفيزياء The Conservation Laws of Physics

من كاسيرر إلى ميكانيكا الكم: تطور مفهوم السببية في الفيزياء والفلسفة

نظرة فلسفية لميكانيكا الكم: هل يمكن فهم الحياة بمفاهيم الفيزياء؟

الطول والزمن في النسبية: التحدي الفيزيائي للفلسفة التقليدية

نسبية الطول بين الفيزياء والفلسفة: أينشتاين في مواجهة فالين