
تاريخ الفيزياء

علماء الفيزياء


الفيزياء الكلاسيكية

الميكانيك

الديناميكا الحرارية


الكهربائية والمغناطيسية

الكهربائية

المغناطيسية

الكهرومغناطيسية


علم البصريات

تاريخ علم البصريات

الضوء

مواضيع عامة في علم البصريات

الصوت


الفيزياء الحديثة


النظرية النسبية

النظرية النسبية الخاصة

النظرية النسبية العامة

مواضيع عامة في النظرية النسبية

ميكانيكا الكم

الفيزياء الذرية

الفيزياء الجزيئية


الفيزياء النووية

مواضيع عامة في الفيزياء النووية

النشاط الاشعاعي


فيزياء الحالة الصلبة

الموصلات

أشباه الموصلات

العوازل

مواضيع عامة في الفيزياء الصلبة

فيزياء الجوامد


الليزر

أنواع الليزر

بعض تطبيقات الليزر

مواضيع عامة في الليزر


علم الفلك

تاريخ وعلماء علم الفلك

الثقوب السوداء


المجموعة الشمسية

الشمس

كوكب عطارد

كوكب الزهرة

كوكب الأرض

كوكب المريخ

كوكب المشتري

كوكب زحل

كوكب أورانوس

كوكب نبتون

كوكب بلوتو

القمر

كواكب ومواضيع اخرى

مواضيع عامة في علم الفلك

النجوم

البلازما

الألكترونيات

خواص المادة


الطاقة البديلة

الطاقة الشمسية

مواضيع عامة في الطاقة البديلة

المد والجزر

فيزياء الجسيمات


الفيزياء والعلوم الأخرى

الفيزياء الكيميائية

الفيزياء الرياضية

الفيزياء الحيوية

الفيزياء العامة


مواضيع عامة في الفيزياء

تجارب فيزيائية

مصطلحات وتعاريف فيزيائية

وحدات القياس الفيزيائية

طرائف الفيزياء

مواضيع اخرى
Orbiting Charges and Multipole Radiation
المؤلف:
Sidney B. Cahn Boris E. Nadgorny
المصدر:
A GUIDE TO PHYSICS PROBLEMS
الجزء والصفحة:
part 1 , p 71
11-8-2016
2038
Orbiting Charges and Multipole Radiation
Charges +q and -q a distance d apart orbit around each other in the x-y plane (z = 0) at frequency ω(d << c/ω) (see Figure 1.1).
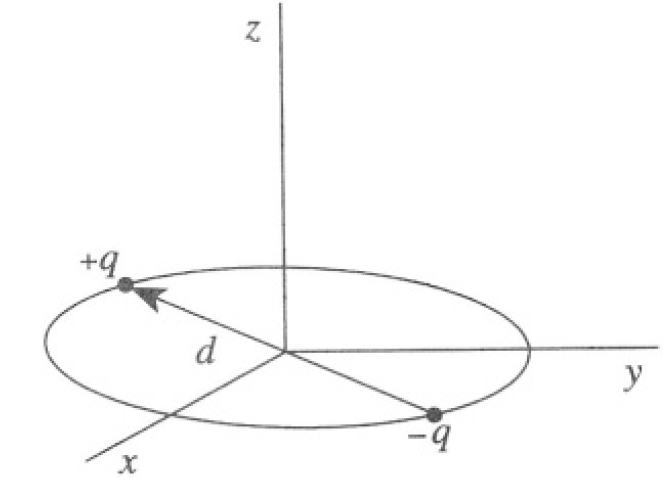
Figure 1.1
a) The emitted radiation is primarily confined to one multipole. Which one?
b) What is the angular distribution of the radiated power?
c) What is the total power radiated?
d) The plane z = -b is now filled with a perfect conductor (b << c/ω) What multipole radiates now?
SOLUTION
a, b) At r >> d the emitted radiation is confined to a dipole where is the wavelength. The vector potential of the system with dipole (r >> λ >> d), moment p at a distance r >> λ is given by
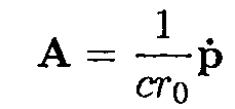
The magnetic field of the system
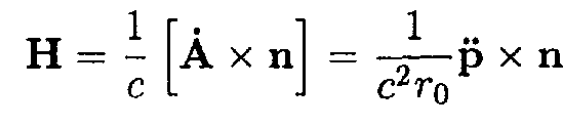 (1)
(1)
where p = qd is the dipole moment of the system, n is the unit vector in the direction of observation, and r0 is the distance from the origin (see
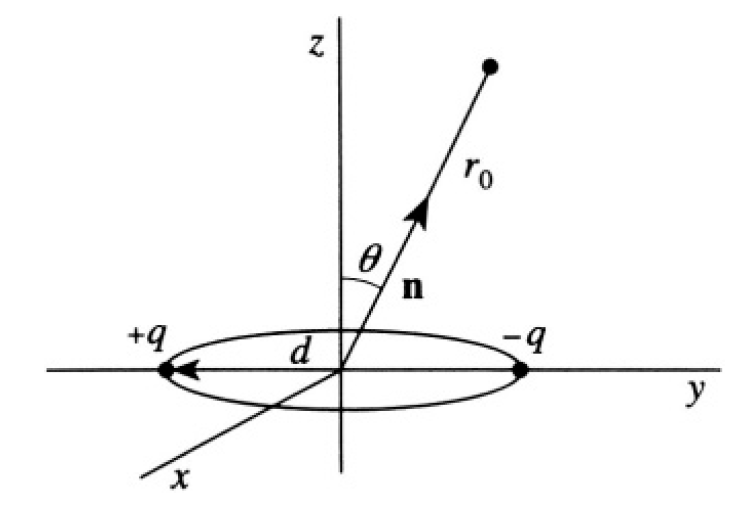
Figure 1.2a
Figure 1.2a). The energy flux is given by the Poynting vector S:
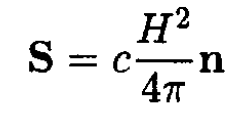 (2)
(2)
The radiated power in a solid angle dΘ is given by
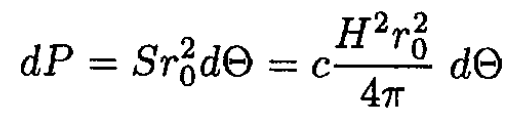 (3)
(3)
Substituting (1) into (3), we obtain
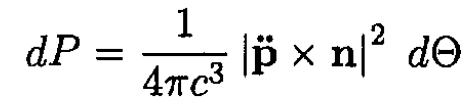 (4)
(4)
Noting that
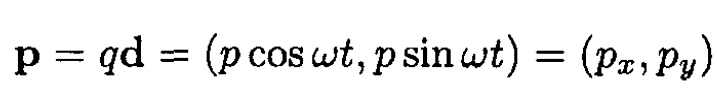
we have
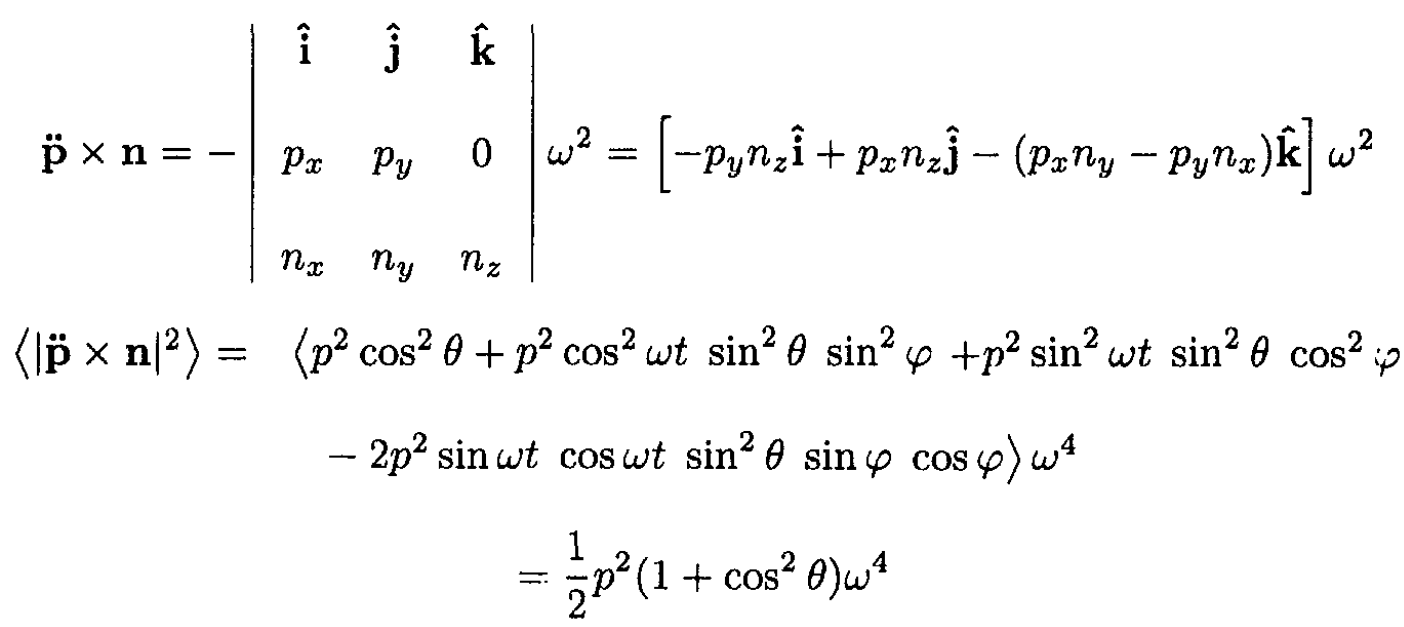
where we took the average over the period of revolution and used [sin2 ωt] = [cos2 ωt] = 1/2 and [2sin ωt cos ωt] = [sin 2ωt] = 0. So form (4)
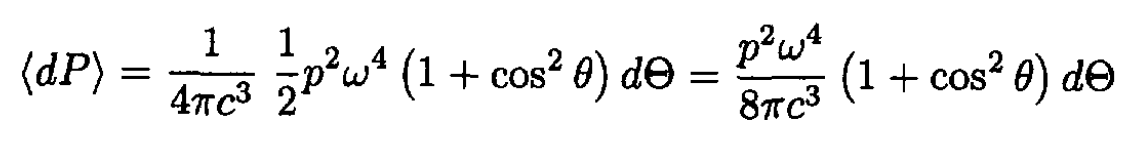
c) The total power radiated is
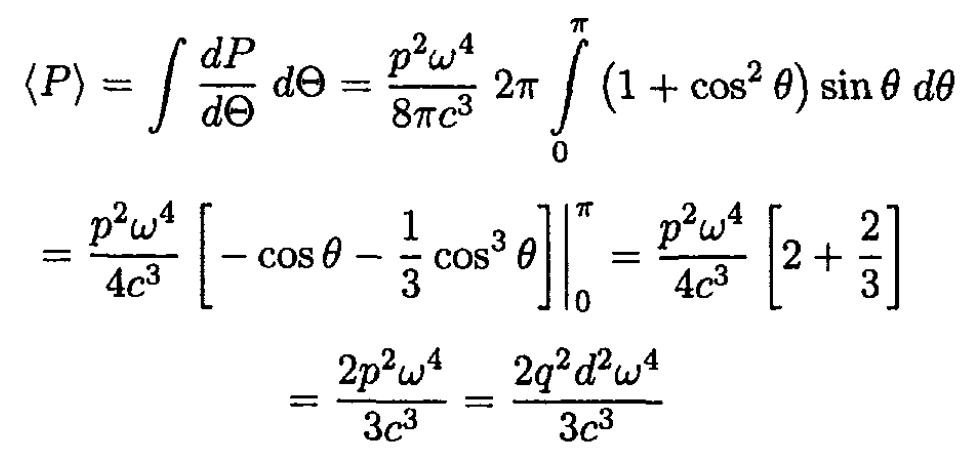
d) When the plane z = -b is filled with a perfect conductor, we have an image charge for each of the charges +q and –q, and the total dipole moment of the system becomes zero (see Figure 1.2b). The next nonzero multipole in this system must be quadrupole with quadrupole moment Dαβ:
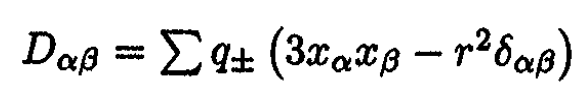
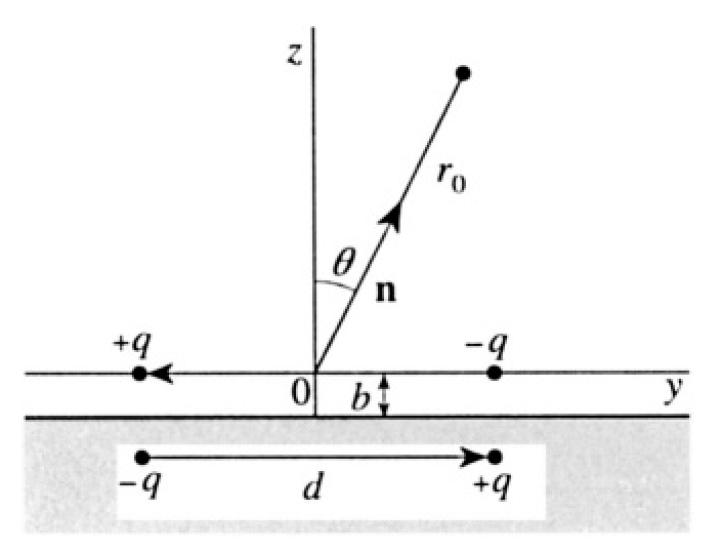
Figure 1.2b
 الاكثر قراءة في مواضيع اخرى
الاكثر قراءة في مواضيع اخرى
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















