
Resistance vs. Capacitance
 المؤلف:
Sidney B. Cahn Boris E. Nadgorny
المؤلف:
Sidney B. Cahn Boris E. Nadgorny
 المصدر:
A GUIDE TO PHYSICS PROBLEMS
المصدر:
A GUIDE TO PHYSICS PROBLEMS
 الجزء والصفحة:
part 1 , p 52
الجزء والصفحة:
part 1 , p 52
 11-8-2016
11-8-2016
 1853
1853
Resistance vs. Capacitance
a) Consider two conductors of some shape. Use them in two alternative ways, as a capacitor and as a resistor as shown in (a) and (b) of Figure 1.1, respectively. In case (a), the space between the conductors is filled with a homogeneous material of permittivity ε, while in case (b), it is filled with a homogeneous material of finite conductivity σ. By considering separately these two cases, prove the relation
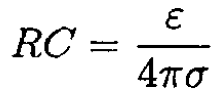
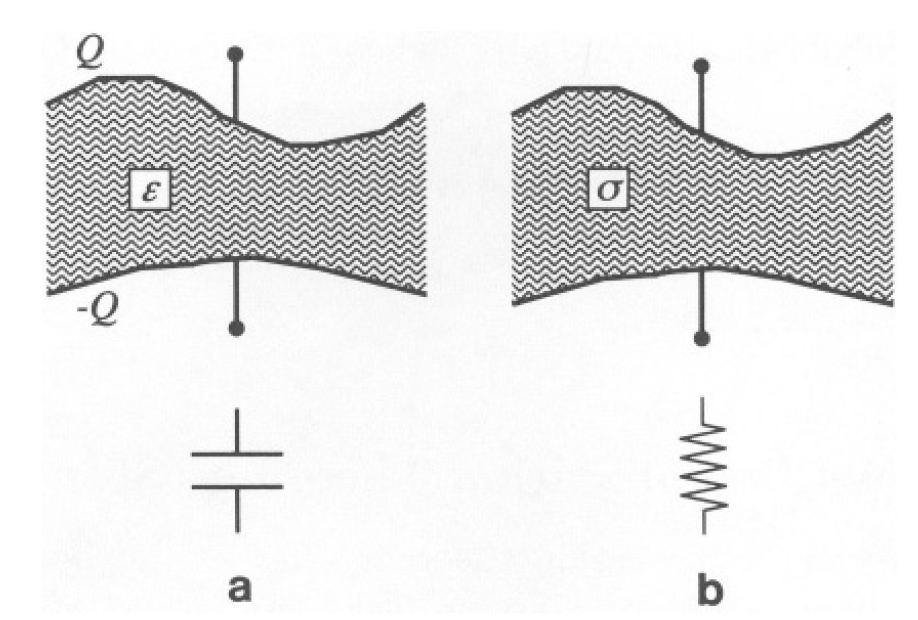
Figure 1.1
between the capacitance C in case (a) and the resistance R in case
(b). If you cannot give a general proof, try at least some special example, e.g., parallel plates.
b) Two conducting spheres have their centers a distance apart. Their respective radii are a and b. Show that when c >> a, b the capacitance of this system will be given approximately by

c) Two small, spherical, perfectly conducting electrodes of radii a and b are embedded in an infinite medium of conductivity σ. Their centers are separated by a distance c >> a, b Find the resistance between them without using (a) and (b).
Hint: If two electrodes at potentials V1 and V2 are embedded in a medium of finite conductivity, the currents I1 and I2 leaving each of them are related to the potentials by the formulae V1 = R11 I1 + R12 I2, V2 = R21 I1 + R22 I2. Determine the coefficients Rij by considering cases with I2 = 0 and I1 = 0.
d) Check the results of (b) and (c) by using (a).
SOLUTION
a) Enclose one of the conductors in a surface and use Maxwell’s equation (see Figures 1.2a and 1.2b)
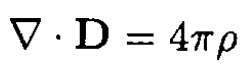
So
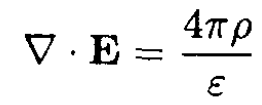 (1)
(1)
Take the volume integral of (1) and transform into a surface integral:
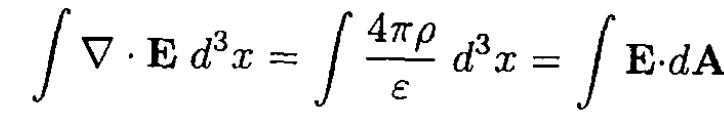 (2)
(2)

Figures 1.2a, b
Using this result and the definition of C, we find
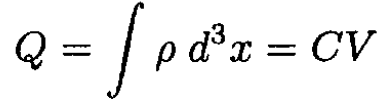
which yields
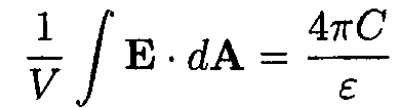 (3)
(3)
Now treat the resistor problem by starting with J = σE. Finding the current flux through the same surface,
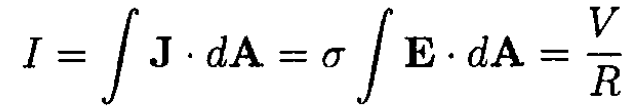
So
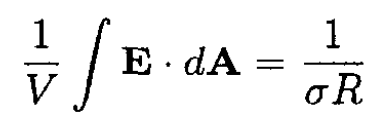 (4)
(4)
Equating (3) and (4), we find
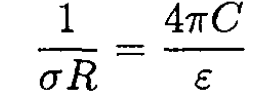
and finally
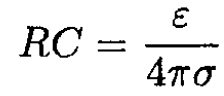 (5)
(5)
The parallel plate capacitor has the following capacitance and resistance:

Thus, we confirm the general result for RC.
b) Find the potential at the surface of each conductor:
 (6)
(6)
So
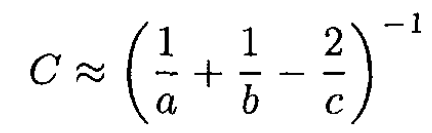 (7)
(7)
c) Following the hint, consider the potential drop from each conductor to infinity when first I2 = 0, and then I1 = 0:

so

In the same fashion
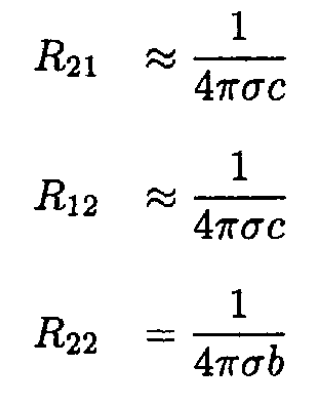
Now, V1 = (R11 – R12)I and V2 = (R21 – R22)I, where I = I1 = -I2. So we obtain for R
 (8)
(8)
d) Multiplying (7) by (8), we find the result in (5) with ε = 1
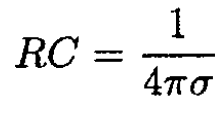
 الاكثر قراءة في مواضيع اخرى
الاكثر قراءة في مواضيع اخرى
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


