Retarded Potential of Moving Line Charge

An infinitely long insulating filament with linear charge density λ lies at rest along the z-axis (see Figure 1.1).

a) Find the electrostatic field E_r at a point P a distance x₀ away from the origin along the x-axis.

b) At t = 0 the wire suddenly starts to move with constant velocity v in the positive direction. Assuming the wire is infinitely thin, write down an expression for the current density J arising from the motion. Using the formula for the retarded potential

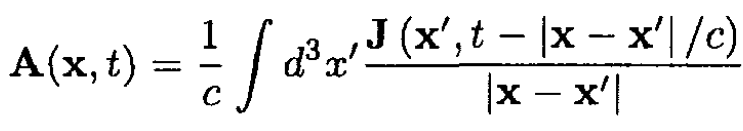
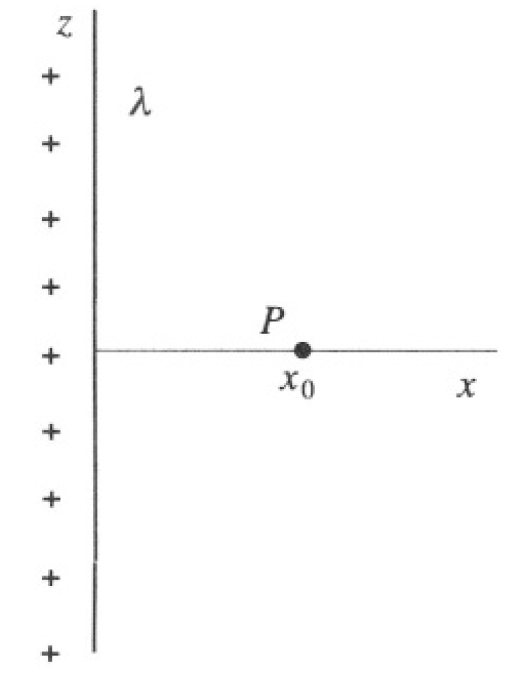
Figure 1.1

Calculate A_z (x₀, t) Give its value for t > x₀/c and for t < x₀/c.

c) Because of cylindrical symmetry, you really know A_z (ρ, t) with ρ the radial coordinate in cylindrical coordinates. Find B (ρ, t) as t →∞. Does your value agree with your intuitive expectation from Ampere’s law?

Hint: A useful integral is

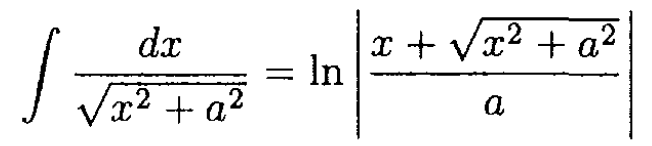
SOLUTION

a) We may calculate the field of a line charge using Gauss’s law

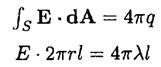
where r is the distance from the line charge and is some length of wire. So

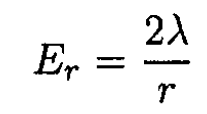(1)

b) The current density

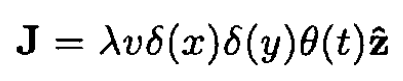(2)

where δ is the Dirac delta function and θ (t) is defined by

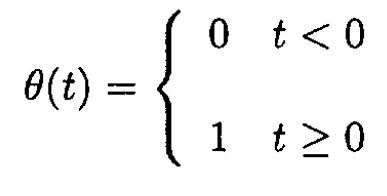
We may then write

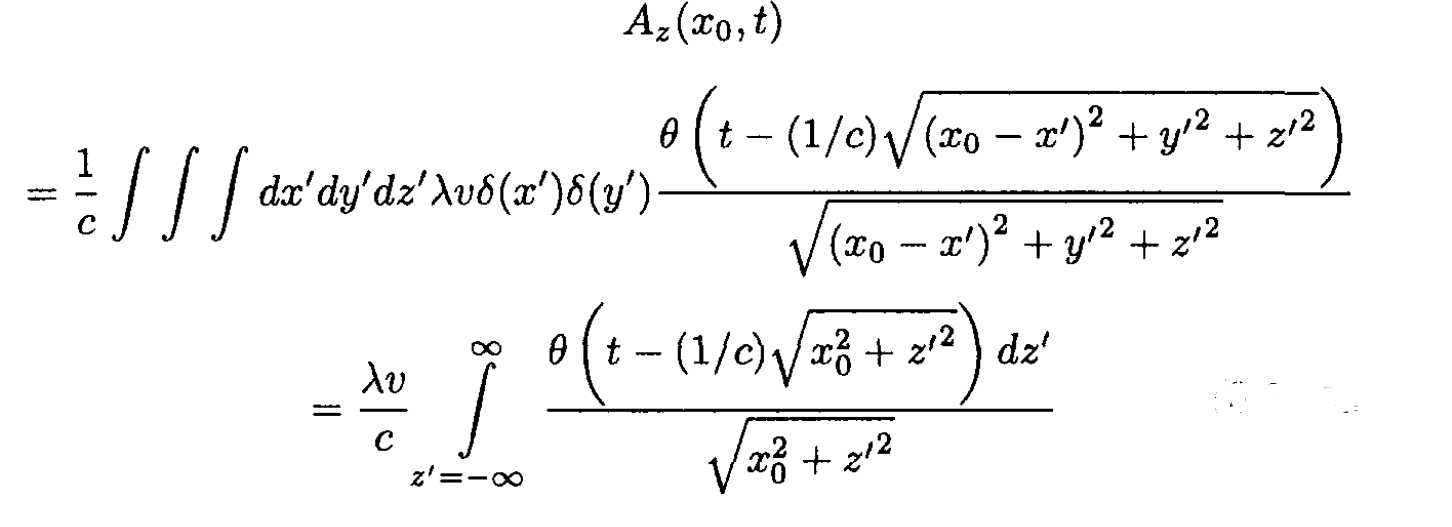(3)

Now, 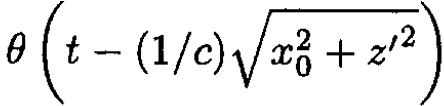is zero unless 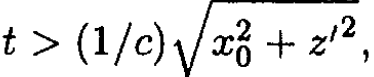so

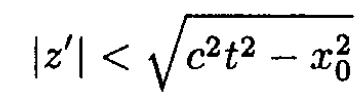
and the integral in (3) becomes

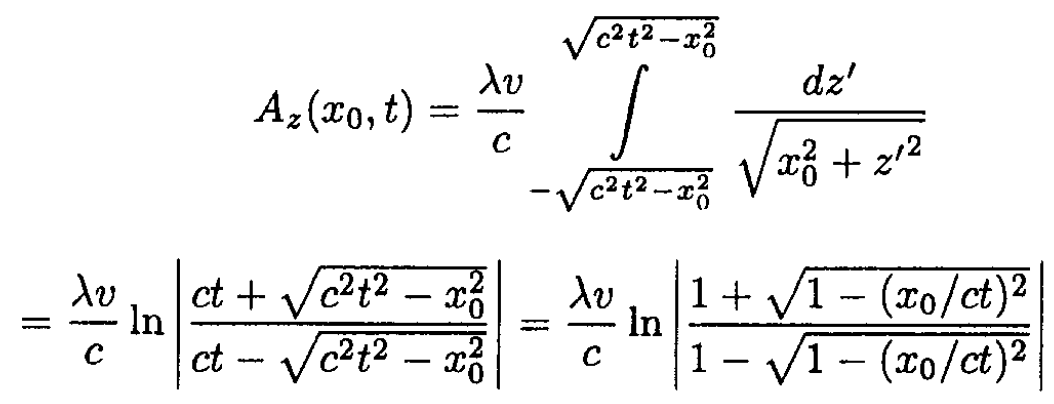(4)

for t > x₀/c. For t < x₀/c, A_z (x₀, t) = 0.

c) From (4), we have for ρ < ct.

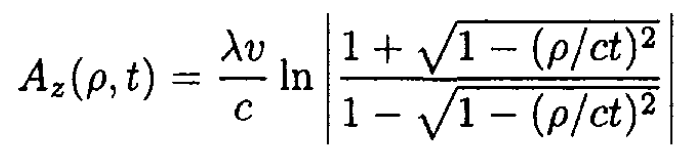(5)

By definition,  which in cylindrical coordinates gives 

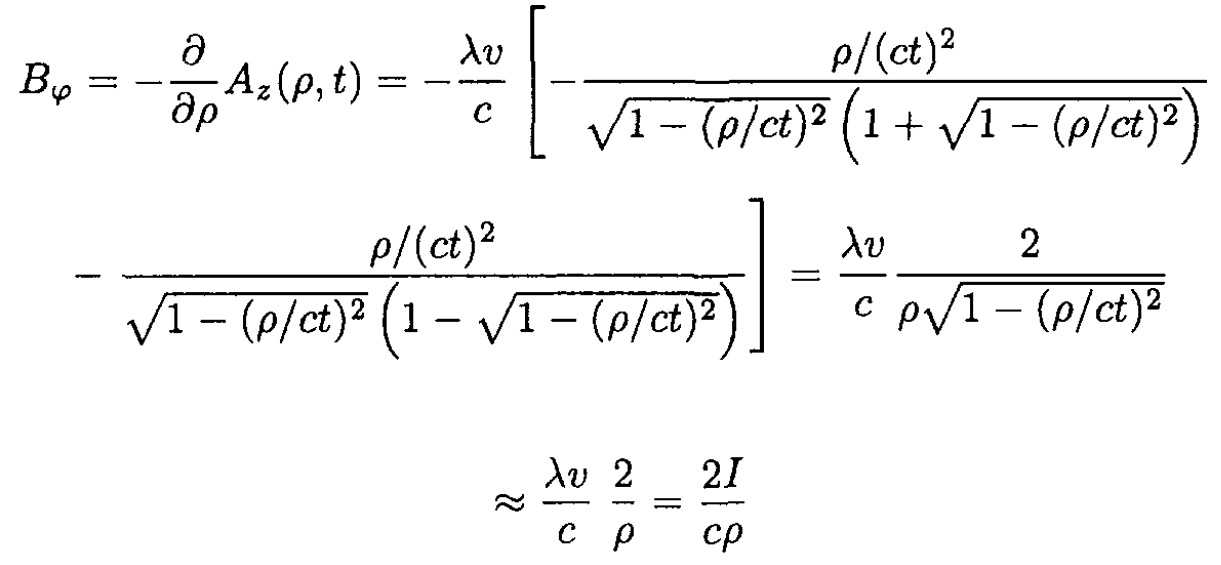
for t → ∞, which is the value of the magnetic field that would result from a calculation using Ampere’s law.