
Given the Eigenfunction
 المؤلف:
Sidney B. Cahn, Gerald D. Mahan And Boris E. Nadgorny
المؤلف:
Sidney B. Cahn, Gerald D. Mahan And Boris E. Nadgorny
 المصدر:
A GUIDE TO PHYSICS PROBLEMS
المصدر:
A GUIDE TO PHYSICS PROBLEMS
 الجزء والصفحة:
part 2 , p 56
الجزء والصفحة:
part 2 , p 56
 18-8-2016
18-8-2016
 1638
1638
Given the Eigenfunction
A particle of mass m moves in one dimension. It is remarked that the exact eigenfunction for the ground state is
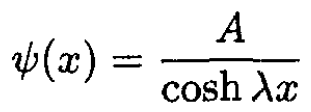 (1)
(1)
where λ is a constant and A is the normalization constant. Assuming that the potential V(x) vanishes at infinity, derive the ground state eigenvalue and V(x).
SOLUTION
We evaluate the second derivative of the eigenfunction, which gives the kinetic energy:
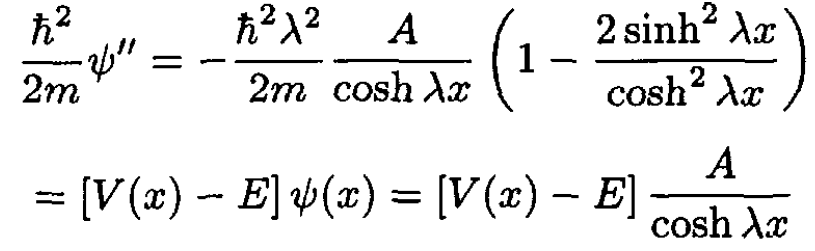 (1)
(1)
We take the limit that x → ∞ of the function on the left, and this must equal –Eѱ since we assumed that the potential vanishes at infinity. Thus, we find that
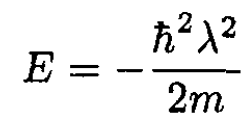 (2)
(2)
The energy is negative, which signifies a bound state. The potential V(x) can be deduced from (1) since everything else in this expression is known:
 (3)
(3)
This potential energy has a bound state which can be found analytically, and the eigenfunction is the function given at the beginning of the problem.
 الاكثر قراءة في مواضيع اخرى
الاكثر قراءة في مواضيع اخرى
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


