
Scattering of Two Electrons
 المؤلف:
Sidney B. Cahn, Gerald D. Mahan And Boris E. Nadgorny
المؤلف:
Sidney B. Cahn, Gerald D. Mahan And Boris E. Nadgorny
 المصدر:
A GUIDE TO PHYSICS PROBLEMS
المصدر:
A GUIDE TO PHYSICS PROBLEMS
 الجزء والصفحة:
part 2 , p 76
الجزء والصفحة:
part 2 , p 76
 21-8-2016
21-8-2016
 1311
1311
Scattering of Two Electrons
Two electrons scatter in a screened environment where the effective potential is
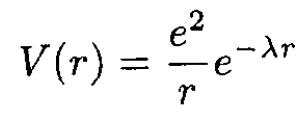 (i)
(i)
where λ is a constant. Consider both electrons in the center-of-mass frame, where both electrons have energy E. This energy is much larger than a Rydberg but much less than mc2, so use nonrelativistic kinematics. Derive an approximate differential cross section for scattering through an angle θ when the two electrons are
a) in a total spin state of S = 0,
b) in a total spin state of S =1.
SOLUTION
We evaluate the scattering in the Born approximation, which is valid when the kinetic energies are much larger than the binding energy. The Fourier transform of the potential is 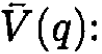
 (1)
(1)
and the formula for the total cross section σ of electrons with initial wave vector k is
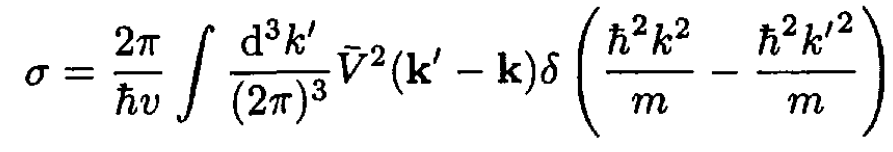 (2)
(2)
This cross section is suitable for classical particles, without regard to spin. The specification to the spin states S = 0, 1 is made below. Write d3 k'= k'2 dk' dΩ where Ω is the solid angle of the scattering. The differential cross section is found by taking the functional derivative of the cross section with respect to this solid angle:
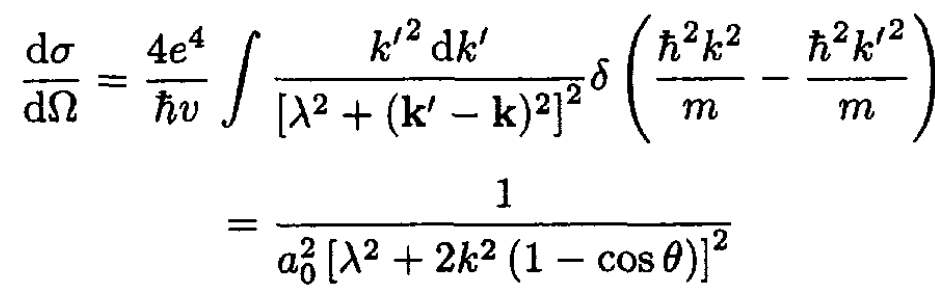 (3)
(3)
where we have used the fact that v = 2hk/m, and k is defined by E = h2k2/2m. The magnitudes of the vectors k' and k are the same, so (k' – k)2 = 2k2 (1 – cos θ). All of the dimensional factors are combined into the Bohr radius a0. Now we consider how this formula is altered by the spin of the electrons. Spin is conserved in the scattering, so the pair of electrons has the same spin state before and after the collision.
a) For S = 0 the two electrons are in a spin singlet which has odd parity. Hence, the orbital state must have even parity. The initial and final orbital wave functions are given below, along with the form of the matrix element. The relative coordinate is r:
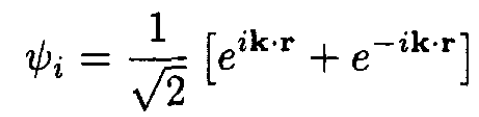 (4)
(4)
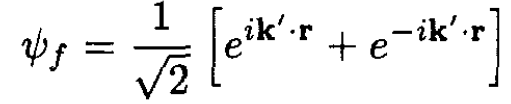 (5)
(5)
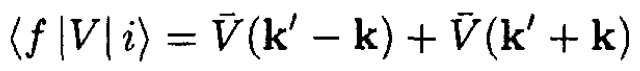 (6)
(6)
 (7)
(7)
The matrix element has two factors.
b) For S = 1 the spins are in a triplet state which has even parity. The orbital part of the wave function has odd parity. There is a minus sign between the two terms in (4) instead of a plus sign, and ditto for the final wave function. Now the differential cross section is
 (8)
(8)
There is a relative minus sign between the two term in the matrix element.
 الاكثر قراءة في مواضيع اخرى
الاكثر قراءة في مواضيع اخرى
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


