Two-Delta-Function Scattering

A free particle of mass m, traveling with momentum parallel to the z-axis, scatters off the potential

Calculate the differential scattering cross section, dσ/dΩ, in the Born approximation. Does this approximation provide a reasonable description for scattering from this potential? In other words, is it valid to use unperturbed wave functions in the scattering amplitude?

SOLUTION

Let us take an unperturbed wave function of the particle of the form

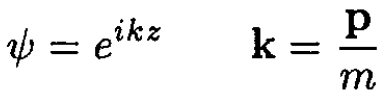(1)

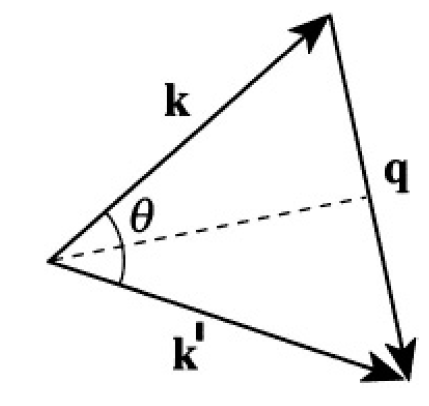
Figure 1.1

Suppose that, after scattering, the wave vector becomes k'. In the Born approximation, the scattering amplitude f (θ) is

(2)

where q = k' - k and q = 2k sin(θ/2) (see Figure 1.1). Substituting the potential V(r) into (2), we obtain

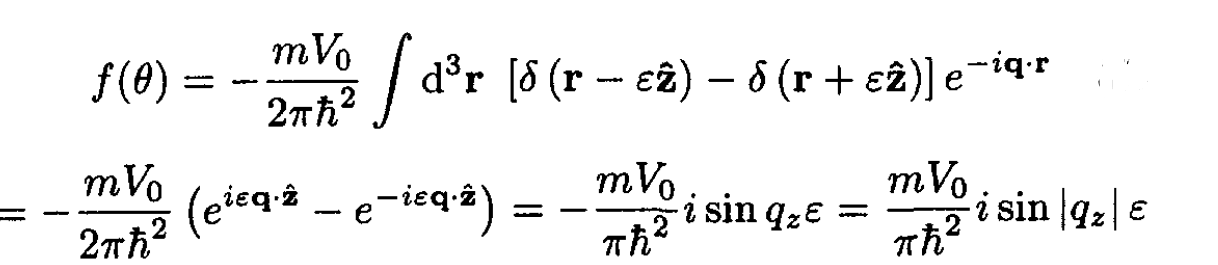(3)

where q_z = -q sin(θ/2) = -2ksin²(θ/2) is the projection of the vector q on the z axis. The scattering cross section

(4)

In order to apply the Born approximation, i.e., to use perturbation theory, we must satisfy at least one of two conditions:

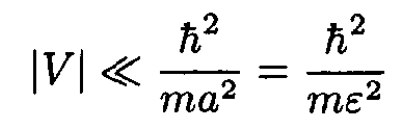(5)

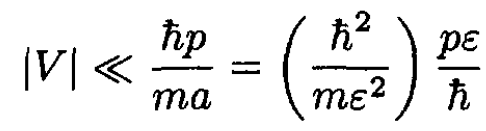(6)

where a = ε is the range of the potential. The first condition derives from the requirement that the perturbed wave function be very close to the unperturbed wave function. Inequality (5) may also be considered the requirement that the potential be small compared to the kinetic energy of the particle localized at the source of the perturbation. Even if the first condition is not satisfied, particles with large enough p will also justify the Born approximation.