
تاريخ الفيزياء

علماء الفيزياء


الفيزياء الكلاسيكية

الميكانيك

الديناميكا الحرارية


الكهربائية والمغناطيسية

الكهربائية

المغناطيسية

الكهرومغناطيسية


علم البصريات

تاريخ علم البصريات

الضوء

مواضيع عامة في علم البصريات

الصوت


الفيزياء الحديثة


النظرية النسبية

النظرية النسبية الخاصة

النظرية النسبية العامة

مواضيع عامة في النظرية النسبية

ميكانيكا الكم

الفيزياء الذرية

الفيزياء الجزيئية


الفيزياء النووية

مواضيع عامة في الفيزياء النووية

النشاط الاشعاعي


فيزياء الحالة الصلبة

الموصلات

أشباه الموصلات

العوازل

مواضيع عامة في الفيزياء الصلبة

فيزياء الجوامد


الليزر

أنواع الليزر

بعض تطبيقات الليزر

مواضيع عامة في الليزر


علم الفلك

تاريخ وعلماء علم الفلك

الثقوب السوداء


المجموعة الشمسية

الشمس

كوكب عطارد

كوكب الزهرة

كوكب الأرض

كوكب المريخ

كوكب المشتري

كوكب زحل

كوكب أورانوس

كوكب نبتون

كوكب بلوتو

القمر

كواكب ومواضيع اخرى

مواضيع عامة في علم الفلك

النجوم

البلازما

الألكترونيات

خواص المادة


الطاقة البديلة

الطاقة الشمسية

مواضيع عامة في الطاقة البديلة

المد والجزر

فيزياء الجسيمات


الفيزياء والعلوم الأخرى

الفيزياء الكيميائية

الفيزياء الرياضية

الفيزياء الحيوية

الفيزياء العامة


مواضيع عامة في الفيزياء

تجارب فيزيائية

مصطلحات وتعاريف فيزيائية

وحدات القياس الفيزيائية

طرائف الفيزياء

مواضيع اخرى
Hot Box and Particle Creation
المؤلف:
Sidney B. Cahn, Gerald D. Mahan And Boris E. Nadgorny
المصدر:
A GUIDE TO PHYSICS PROBLEMS
الجزء والصفحة:
part 2 , p 35
29-8-2016
1699
Hot Box and Particle Creation
The electromagnetic radiation in a box of volume V can be treated as a noninteracting ideal Bose gas of photons. If the cavity also contains atoms capable of absorbing and emitting photons, the number of photons in the cavity is not definite. The box is composed of a special material that can withstand extremely high temperatures of order τ >> τe = me c2.
a) Derive the average number of photons in the box.
Hint:
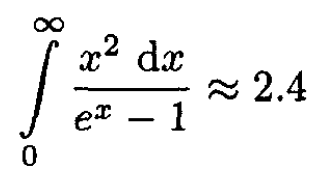
b) What is the total energy of the radiation in the box for τ/τe << 1?
c) What is the entropy of the radiation for τ/τe << 1?
d) Assume that photons can create neutral particles of mass m and zero spin and that these neutral particles χ can create photons by annihilation or some other mechanism. The cavity now contains photons and particles in thermal equilibrium at a temperature τ. Find the particle density n = N/V. Consider only the process where a single photon is emitted or absorbed by making a single particle.
Hint: Minimize the free energy.
Now, instead of neutral particles, consider the creation of electron-positron pairs.
e) What is the total concentration of electrons and positrons inside the box when τ/τe << 1?
f) What is the total concentration of electrons and positrons when τ/τe >> 1?
Hint:
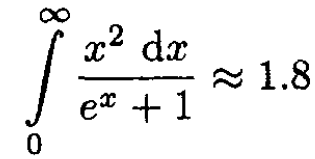
SOLUTION
a) The number of photons is
 (1)
(1)
where the factor 2 comes from the two polarizations of photons; p = hk = hω/c. So,
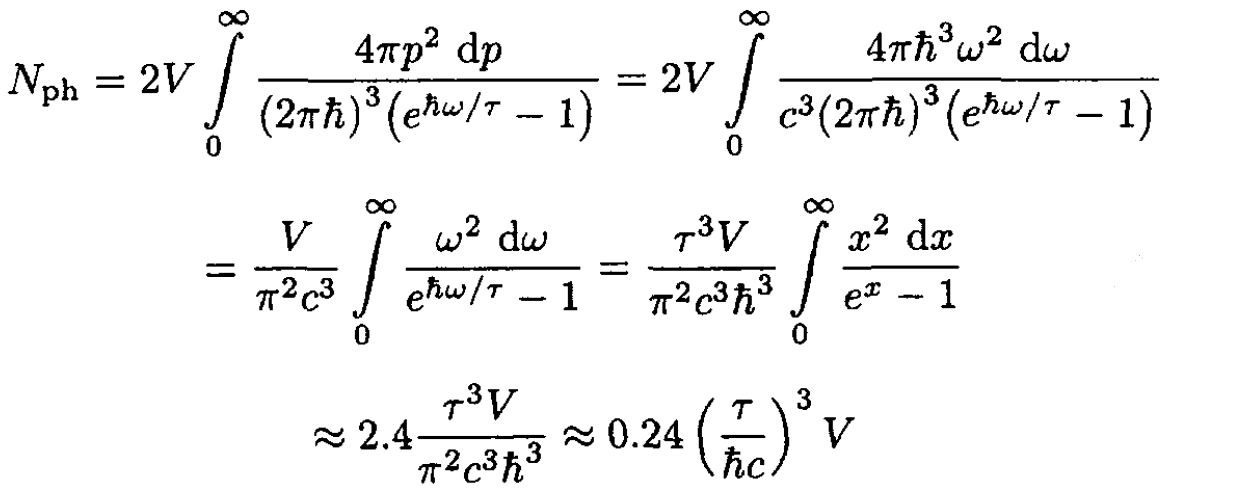 (2)
(2)
b) At low temperatures we can disregard any interaction between photons due to the creation of electron–positron pairs. We can therefore use the standard formula for energy flux:
 (3)
(3)
where σ is the Stefan–Boltzmann constant. On the other hand, by analogy with molecular flow,
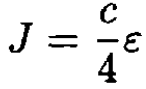 (4)
(4)
where ε = E/V is the energy density. So,
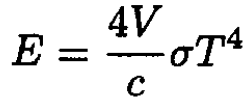 (5)
(5)
c) Using the equation of state for a photon gas
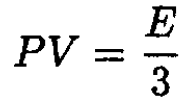 (6)
(6)
and
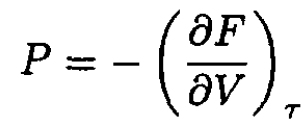 (7)
(7)
we have
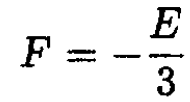 (8)
(8)
The entropy S is then
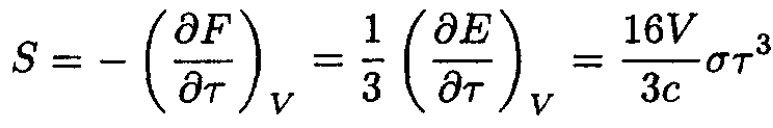 (9)
(9)
d) The energy E of the system of particles + photons is
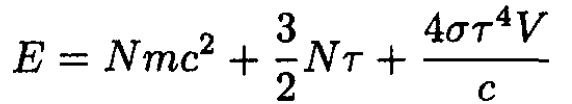 (10)
(10)
The entropy of the system is the sum of the entropy of an ideal gas and radiation. The free energy of a single-particle ideal gas with s = 0 of created particles and the radiation is then
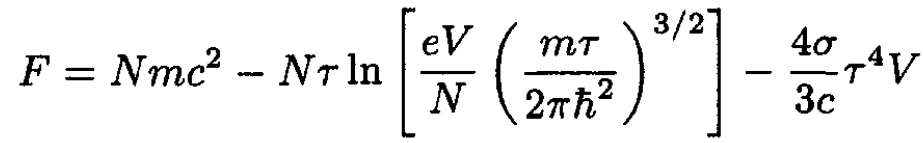 (11)
(11)
Minimizing the free energy with respect to the number of particles, we have
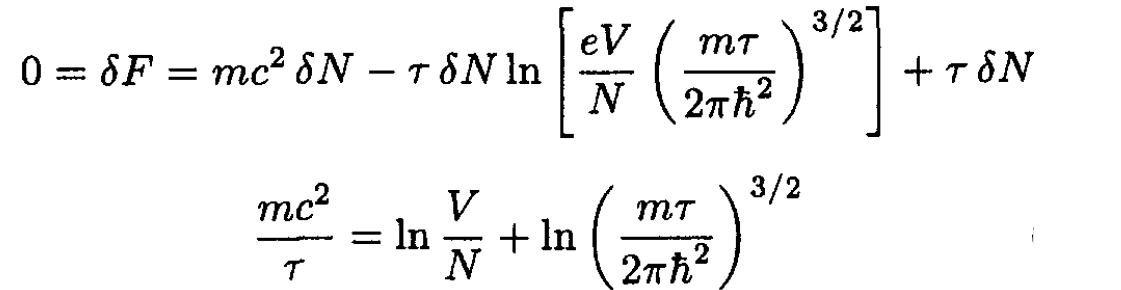 (12)
(12)
From (12) we obtain
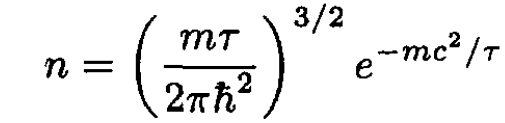 (13)
(13)
This result can be immediately obtained if we consider the process as a “chemical” reaction
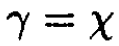
or

For chemical equilibrium
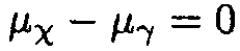
Since, for photons, μ = 0, we have
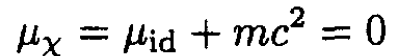
where μid is the chemical potential of an ideal gas (see part (e)). This result gives us (13).
e) Pair creation and annihilation can be written in the form
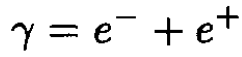 (14)
(14)
The chemical potential μ of the photon gas is zero (since the number of photons is not constant but is defined by equilibrium conditions). Therefore, we have for process (14) in equilibrium:
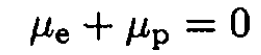 (15)
(15)
where μe and μp are the chemical potentials of electrons and positrons, respectively. If we disregard the walls of the box and assume that there are no electrons inside the box initially, then the number of electrons equals the number of positrons, and μe = μp = 0 We then find for the number of electrons (positrons)
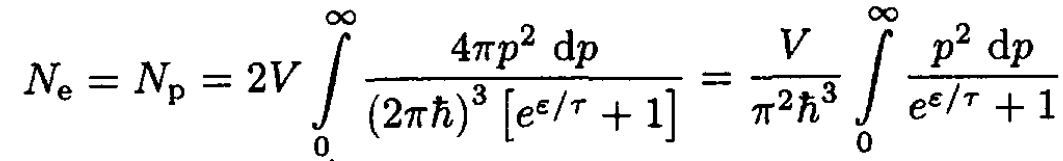 (16)
(16)
where the factor 2 comes from the double degeneracy of the electron gas g = 2s + 1, and we set μ = 0. The energy may be written
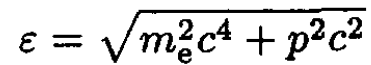
Disregarding the 1 in the denominator of (16) and expanding the square root with respect to the small parameter p2/m2ec2, for τ << mec2 we obtain, from (16),
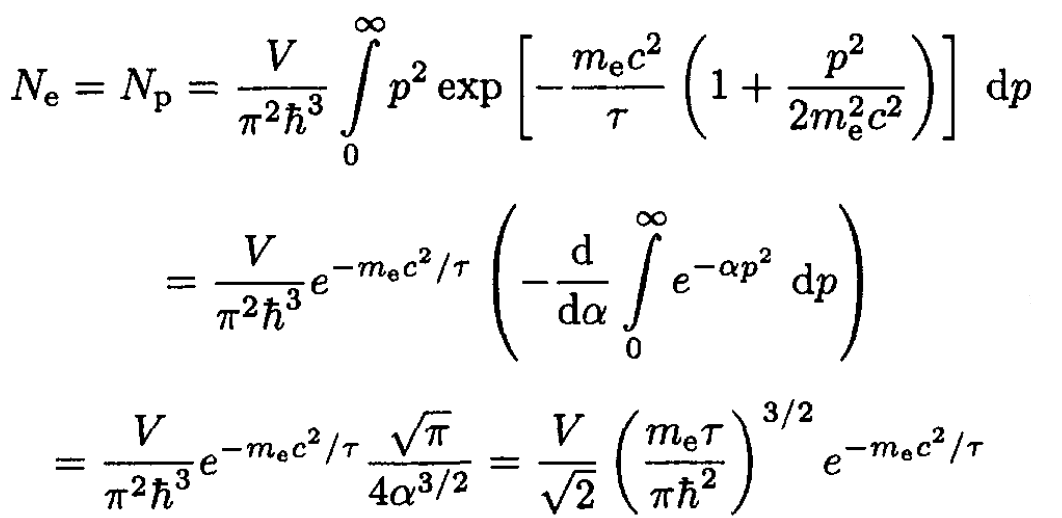 (17)
(17)
where we set α ≡ 1/2meτ. We then find that the concentrations are
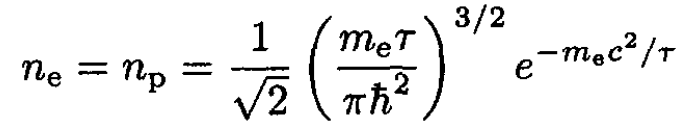 (18)
(18)
and so
 (19)
(19)
Alternatively, we can take an approach similar to the one in (d). Using the formula for the chemical potential of an ideal gas gives
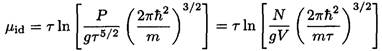 (20)
(20)
We can immediately write
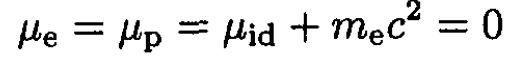
to obtain the same result in (18) and (19).
f) For τ >> mec2 the electrons are highly relativistic, and we can write ε = cp in (16). Then
 (21)
(21)
where we have used the integral given in the problem. Finally,
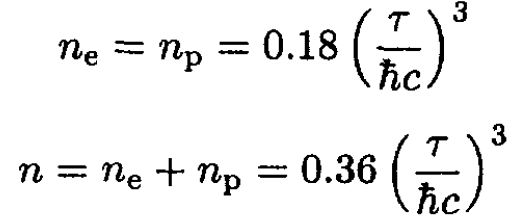 (22)
(22)
 الاكثر قراءة في مواضيع اخرى
الاكثر قراءة في مواضيع اخرى
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















