
Osmotic Pressure
 المؤلف:
Sidney B. Cahn, Gerald D. Mahan And Boris E. Nadgorny
المؤلف:
Sidney B. Cahn, Gerald D. Mahan And Boris E. Nadgorny
 المصدر:
A GUIDE TO PHYSICS PROBLEMS
المصدر:
A GUIDE TO PHYSICS PROBLEMS
 الجزء والصفحة:
part 2 , p 28
الجزء والصفحة:
part 2 , p 28
 30-8-2016
30-8-2016
 1699
1699
Osmotic Pressure
Consider an ideal mixture of N0 monatomic molecules of type A and N2 monatomic molecules of type B in a volume V.
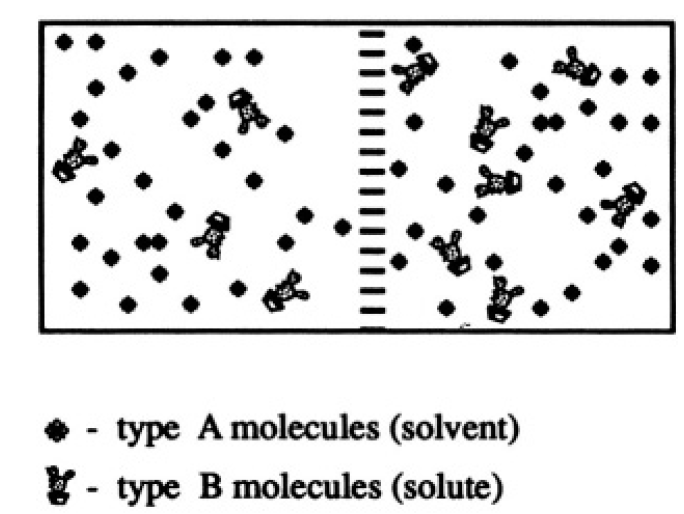
Figure 1.1
a) Calculate the free energy F(τ, V, N0, N1). Calculate the Gibbs potential G(τ, P, N0, N1). G is the Legendre transform of F with respect to V.
b) If N0 >> N1 the molecules of type A are called the solvent, and those of type B the solute. Consider two solutions with the same solvent (type A) and different concentrations of solute (type B molecules) separated by a partition through which solvent molecules can pass but solute molecules cannot (see Figure 1.1). There are N0 particles in volume V (or 2N0 in volume 2V), and N1 and N2 particles in volume V on the left and right of the membrane, respectively. Calculate the pressure difference across the membrane at a given temperature and volume. Assume that the concentrations of the solutions are small; i.e.,
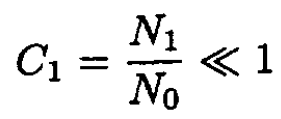
and
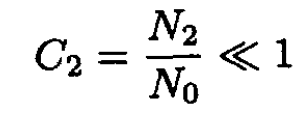
SOLUTION
a) The free energy for a one-component ideal gas is
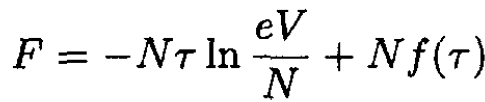 (1)
(1)
The Gibbs free energy
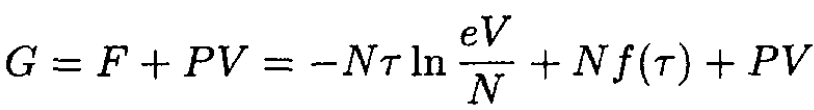 (2)
(2)
But G = G(τ, V, N), so (2) must be transformed:
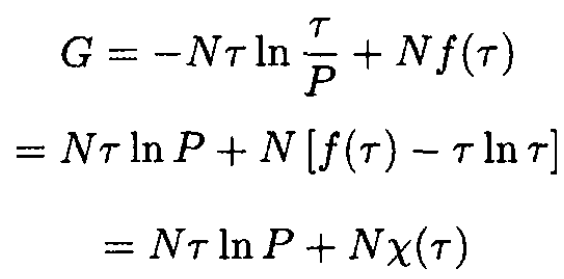 (3)
(3)
If we have a mixture of two types of molecules with N0 and N1 particles each, we find for the thermodynamic potential of the mixture:
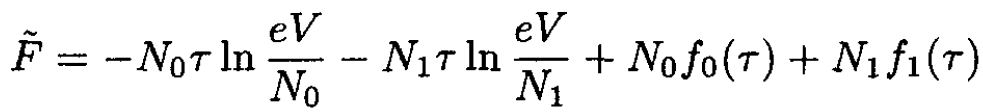 (4)
(4)
Therefore 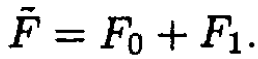 The Gibbs potential of the mixture
The Gibbs potential of the mixture
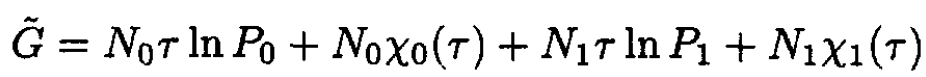 (5)
(5)
where P0, P1 are partial pressures (P = P1 + P2) corresponding to particles A and B, respectively. So,
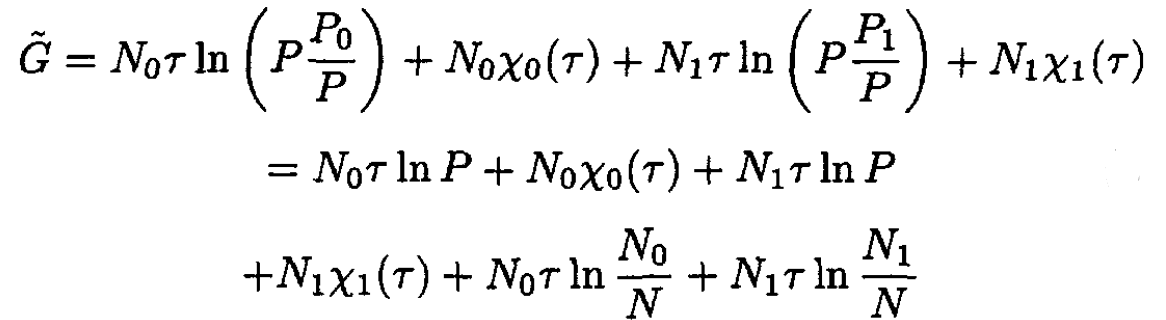 (6)
(6)
It can be seen that
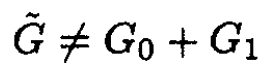
namely
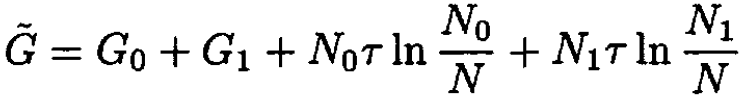 (7)
(7)
where N = N0 + N1.
b) To derive the pressure difference, we notice that for the system with a semipermeable membrane, only the chemical potentials of the solvent are equal, whereas the chemical potentials of the solute do not have to be (since they cannot penetrate through the membrane). We will write first the Gibbs free energy on the left and right of the membrane, 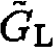 and
and 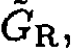 respectively.
respectively.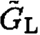 will be defined by (6), with P → PL, whereas
will be defined by (6), with P → PL, whereas
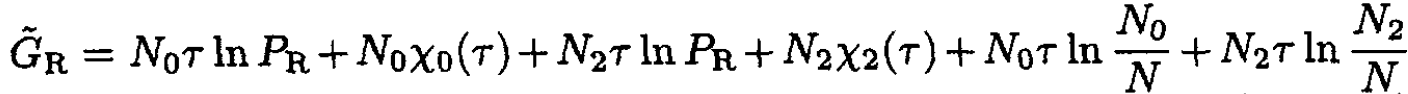 (8)
(8)
The chemical potentials of the solvent are given by
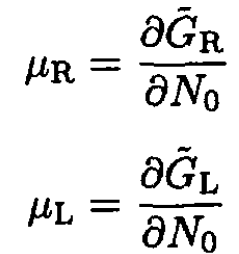 (9)
(9)
Equating μR = μL, we obtain
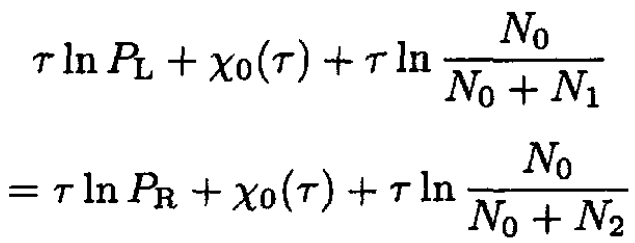 (10)
(10)
or
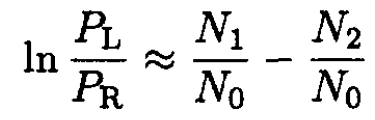 (11)
(11)
where we only take into account the first-order terms in the solute. If we also assume, which is usually the case, that the osmotic pressure is also small, i.e., 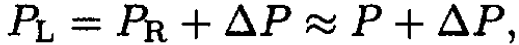 we obtain, from (11),
we obtain, from (11),
 (12)
(12)
where C1 and C2 are the concentrations of the solutes: C1 ≡ N1/N0; C2 ≡ N2/N0. Therefore, with the same accuracy, we arrive at the final formula:
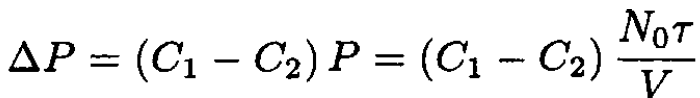 (13)
(13)
A different derivation of this formula may be found in Landau and Lifshitz.
 الاكثر قراءة في مواضيع اخرى
الاكثر قراءة في مواضيع اخرى
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


