


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
أقرأ أيضاً
التاريخ: 26-8-2016
التاريخ: 10-9-2016
التاريخ: 6-9-2016
التاريخ: 22-8-2016
|
غياث الدين الكاشي
(... – 1344م)
غياث الدين جمشيد بن مسعود بن محمود بن محمد الكاشي (وقيل الكاشاني)، ولد في اواخر القرن الثامن الهجري في مدينة كاشان، وتوفي عام 839هـ، عرف بكثرة طوافه في املدن لطلب العلم ونهل المعرفة، ولذلك تنوعت معارفه فدرس العلوم في اماكن شتى من فارس، شهر بحبه لقراءة القران الكريم فكان بقرا القران مرة كل يوم، وهو امر برز في اسلوبه الكتابي بعد ذلك درس النحو والصرف والفقه على مذاهب الائمة الاربعة فاجاد فيها وتمكن منها واصبح حجة فيها، استفاد من معرفته بالمنطق فانكب على دراسة تواليف الرياضيات يلتهمها التهاما مما ادهش علماء الرياضيات لقدرته على الاستيعاب وحسن التعبير، وقد كان ولعه بالرياضيات عن كون ابيه من اكبر علماءؤ الرياضيات والفلك، فنشأ ابنه غياث الدين في كنفه العلمي، يقول الكاشاني في تقديمه لكتابه (نزهة الحدائق) : سالني بعض الاخوان، هل يمكن عمل الة يعرف منها تقاويم الكواكب. وعروضها ام لا، فابتكرت فيه حتى وفقني الله تعالى، والهمني به، وظفرت عليه ان ارسم صفحة واحدة من صحيفة يعرف منها تقاويم الكاوكب السبعة وعروضها وابعادها عن الارض، وعمل الخسوف والكسوف بأسهل طريق واقرب زمان، ثم استنبطت منها انواعا مختلفة يعرف من كل واحد منها ما يعرف من الاخر، والفت هذه المسالة مشتملة على كيفية عملها، وكيفية العمل بها، وسميت الة بطبق المناطق، والرسالة بنزهة الحدائق، والحقت بها عمل الالة المسماة بلوح الاتصالات، وهي ايضا مما اخترعت عملها قبل هذه العصمة والتوفيق وهي مشتملة على بابين وخاتمة ومن المؤسف ان علماء الغرب يدعون ان كلبر الرياضي الفلكي هو الذي اثبت ان مسارات الكواكب اهليليجية وليست دائرية، ونسوا ان الكاشاني اثبت ذلك في كتابه نزهة الحدائق واعطى شرحا مفصلا لكيفية رسم اهليليجي القمر وعطارد قبله باكثر من مائة عام.
الكاشاني والنسبة التقريبية
بحث الكاشي في تعيين النسبة التقريبية، فأثبت قيمة تلك النسبة الى درجة من التقريب تفوق من سبقه بكثير وقيمتها : 3.1415926535898732 وكان ليوناد فيبوناشي الذي جاء قبل الكاشي بنحو مائة عام قد درس قيمة النسبة التقريبية فحصل على نسبة محيط الدائرة الى قطرها بما قدره 3.141818.
الكسور العشرية
كان لابتكار الكاشي الكسور العشرية اثر عظيم في دفع تقدم الحساب واختراع الالات الحاسبة، فقد استخدم للمرة الاولى الصفر تماما للاغراض نفسها التي نعرفها ونتناولها في عصرنا الحاضر، يقول يوجين سميث في تاريخ الرياضيات ان الخلاف بين علماء الرياضيات كبير، ولكن اتفق اكثرهم على ان الكاشي هو الذي ابتكر الكسر العشري.
وذكر ديرك سترويك في كتاب مصادر الرياضيات قال : ان غياث الدين الكاشي هو صاحب فكرة الكسر العشري، ويظهر ذلك في كتابه مفتاح الحساب الذي حوى للمرة الاولى على الكثير من المسائل التي تستعمل الكسور العشرية.
نظرية الاعداد :
توصل العلماء العرب المسلمين بدراستهم الاعداد الطبيعية الى قوانين عدة في مجموع الاعداد الطبيعية المرفوعة الى القوة الاولى والثانية والثالثة، وقد زاد الكاشي على من سبقه بدراسة نظرية الاعداد، فبرهن قانونا لمجموع الاعداد الطبيعية المرفوعة الى القوة الرابعة، ذكر هذا القانون ديفيد سميث في تاريخ الرياضيات واشار اليه على انه التالي :
ونجد في احد كتب الكاشي قانونا لايجاد مجموع الاعداد الطبيعية المرفوعة الى القوة الرابعة، اما القانون فهو :
مجــ ب 4 = م جــ ب – 1 + مجــ ب) مجــ ب2
مجموع ن4 = مجموع ب +أ/2 + مجموع ب2
ويمكن توضيح فكرة هذا القانون اذا اعتبرنا الاتي :
مجموع ن4 = 41 + 42 + 43 + ...+ن2
مجموع ب2 = 21 + 22 + 23 + ... +ب2
مجموع ب = 1+2+3+...+ب
إن قانون مجموع الاعداد الطبيعية المرفوعة الى القوة الرابعة لعب دوراً اساسيا في تطوير علم الاعداد، كان غياث الدين يعتمد في بدء بحوثه على الجداول الرياضية التي وضعها السابقون من المسلمين لايجاد حدود المعادلة الجبرية، ولكنه ما عتم ان استخدم القاعدة العادة لنظرية ذات الحدين – وهي التي ابتكرها عمر الخيام من قبل لأي أسس صحيح مثل :
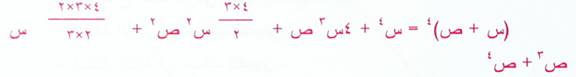
ويكون الكاشي بهذا قدر طور نظرية ذات الحدين غير ان علماء الغرب اعتبروا اسحاق نيوتن هو مبتكر هذه النظرية، وحقيقة الامر ان نيوتن لم يزد على تعميم هذه النظرية التي عممها الكاشي أي اسس حقيقي (كسر او عدد صحيح موجب او اسالب) مثل :
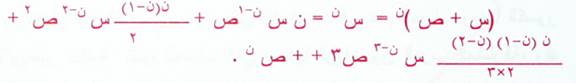
ولكنت دريك سترويك يعترف بأسبقية الكاشي في تعميم النظرية، فيقول : ان الكاشي اول من فكر في نظرية ذات الحدين، ويرجع اليه الفضل في تطوير خواص معاملاتها. ويعود الفضل في انشاء مرصد سمرقند ويرجع الى غياث الدين وقاضي زادة الرومي، وبعد وفاة الاثنين اكمل المرصد على القرشجي.
وفي الهندسة حذا حذو اقليدس في هذا العلم في نقضه لفرضية اقليدس الخامسة، واستخدم هذا في جميع مصنفاته المقاييس والاطوال التالية : الفرسخ، القصبة، الذراع، الاصبع وعرض حبة الشعير ، فكان الفرسخ = 2000 قصبة، والقصبة = 6 أذراع، والذراع = 24 إصبع، والإصبع = عرض حبه الشعير.
وفي علم المثلثات درس الكاشي تواليف المتقدمين من علماء الاسلام، وشرح وعلق على انتاجهم، وقد حسب جداول لجيب الدرجة الاولى، استخدم في ذلك معادلة ذات الدرجة الثالثة في معادلاته المثلثية، وهو ما توضح في رسالته المعنونة استخراج جيب الدرجة الاولى، يقول الكاشي فيها : اقول .. اذا علم جيب قوس، واريد معرفة جيب امثالها، يضرب مكعب ك الجيب في اربع ثوان، وينقص الحاصل من ثلاثة امثاله، فالباقي هو الجيب المطلوب، وصورة ما اراده الكاشي ما يلي :
جا3س = 4 جاس3 – 3جاس
مصنفات غياث الدين الكاشي :
ونؤكد ان هذا الكتاب يتضمن بعض الابتكارات في علم الحساب ومنها العشرية، ويعتبر خاتمة كتب الحساب التي صنفها الرياضيون العرب المشارقة، وقد اختصره اولوغ بك واسماه تلخيص المفتاح.
كتاب زيج الخاقاني (تصحيح زيج الابلخاني للطوسي). او ما يسمى (كتاب زيج الخاقاني تكميل الأيلخاني).



|
|
|
|
دراسة تحدد أفضل 4 وجبات صحية.. وأخطرها
|
|
|
|
|
|
|
جامعة الكفيل تحتفي بذكرى ولادة الإمام محمد الجواد (عليه السلام)
|
|
|