
تاريخ الفيزياء

علماء الفيزياء


الفيزياء الكلاسيكية

الميكانيك

الديناميكا الحرارية


الكهربائية والمغناطيسية

الكهربائية

المغناطيسية

الكهرومغناطيسية


علم البصريات

تاريخ علم البصريات

الضوء

مواضيع عامة في علم البصريات

الصوت


الفيزياء الحديثة


النظرية النسبية

النظرية النسبية الخاصة

النظرية النسبية العامة

مواضيع عامة في النظرية النسبية

ميكانيكا الكم

الفيزياء الذرية

الفيزياء الجزيئية


الفيزياء النووية

مواضيع عامة في الفيزياء النووية

النشاط الاشعاعي


فيزياء الحالة الصلبة

الموصلات

أشباه الموصلات

العوازل

مواضيع عامة في الفيزياء الصلبة

فيزياء الجوامد


الليزر

أنواع الليزر

بعض تطبيقات الليزر

مواضيع عامة في الليزر


علم الفلك

تاريخ وعلماء علم الفلك

الثقوب السوداء


المجموعة الشمسية

الشمس

كوكب عطارد

كوكب الزهرة

كوكب الأرض

كوكب المريخ

كوكب المشتري

كوكب زحل

كوكب أورانوس

كوكب نبتون

كوكب بلوتو

القمر

كواكب ومواضيع اخرى

مواضيع عامة في علم الفلك

النجوم

البلازما

الألكترونيات

خواص المادة


الطاقة البديلة

الطاقة الشمسية

مواضيع عامة في الطاقة البديلة

المد والجزر

فيزياء الجسيمات


الفيزياء والعلوم الأخرى

الفيزياء الكيميائية

الفيزياء الرياضية

الفيزياء الحيوية

الفيزياء العامة


مواضيع عامة في الفيزياء

تجارب فيزيائية

مصطلحات وتعاريف فيزيائية

وحدات القياس الفيزيائية

طرائف الفيزياء

مواضيع اخرى
Teacup Engine
المؤلف:
Sidney B. Cahn, Gerald D. Mahan And Boris E. Nadgorny
المصدر:
A GUIDE TO PHYSICS PROBLEMS
الجزء والصفحة:
part 2 , p 6
6-9-2016
1471
Teacup Engine
was peacefully drinking tea at five o’clock galactic time, as was his wont, when he had an emergency outside the shuttle, and he had to do an EVA to deal with it. Upon leaving the ship, his jetpack failed, and nothing remained to connect him to the shuttle. Fortunately, he had absentmindedly brought his teacup with him. Since this was the only cup he had, he did not want to throw it away in order to propel him back to the shuttle (besides, it was his favorite cup). Instead, he used the sublimation of the frozen tea to propel him back to the spaceship (see Figure 1.1). Was it really possible? Estimate the time it might take him to return if he is a distance L = 40 m from the ship. Assume that the sublimation occurs at a constant temperature T = 273 K.
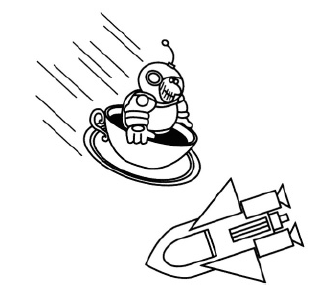
Figure 1.1
The vapor pressure at this temperature is P0 = 600Pa, and the total mass of the astronaut M = 110 kg.
SOLUTION
If the cup were vacuum tight, the number of molecules leaving the surface would be the same as the number of molecules returning to the surface. The mass flow rate of the molecules hitting the surface is
 (1)
(1)
where ρ0 is the vapor density corresponding to the saturation, (v) is the average velocity of the molecules, and A is the surface area of the ice. The mass flow rate of the molecules actually returning to the surface is
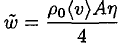 (2)
(2)
where η is the sticking coefficient (the probability that the molecule hitting the surface will stick to it). Let us assume for now that η = 1 (we will see later that this is not true, but that actually gives us the lower limit of the distance). If the cup is open we can assume that the number of molecules leaving the surface is the same as in the closed cup, but there are few returning molecules. We then find that the time τ for complete evaporation of the ice is
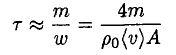 (3)
(3)
where we take m ~ 200 g as the mass of the ice, A ~ 30 cm2, and
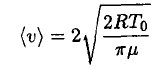 (4)
(4)
Substituting (4) into (3), we obtain
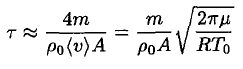 (5)
(5)
Once again using the ideal gas law, we may obtain ρ0:
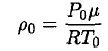 (6)
(6)
Substituting (6) into (5) yields
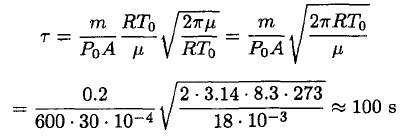 (7)
(7)
During the sublimation of the ice, the acceleration of the astronaut is
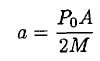 (8)
(8)
where P0A/2 corresponds to the momentum transferred by the molecules leaving the surface. Using the time τ calculated above, he will cover a distance
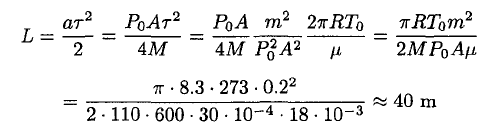 (9)
(9)
Note that this is the lower limit because we assumed η = 1 and that all the molecules that are leaving go to infinity. So, it seems that the astronaut can cover the distance to the ship by using his cup as an engine. Moreover, the sticking coefficient η, which is often assumed to be close to unity, could be much smaller (for water, η ~ 0.03 at 0°C). That explains why the water in a cup left in a room does not evaporate in a matter of minutes but rather in a few hours. For a detailed discussion see E. Mortensen and H. Eyring, J. Phys. Chem. 64, 846 (1960). The physical reason for such a small sticking coefficient in water is based on the fact that in the liquid phase the rotational degrees of freedom are hindered, leading to a smaller rotational partition function. So, the molecules whose rotation cannot pass adiabatically into the liquid will be rejected and reflect back into the gaseous phase. These effects are especially strong in asymmetric polar molecules (such as water). The actual time the teacup engine will be working is significantly longer (about 30 times, if we assume that the sticking coefficient for ice is about the same as for water at 0oC).
 الاكثر قراءة في مواضيع اخرى
الاكثر قراءة في مواضيع اخرى
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام) قسم الشؤون الفكرية يصدر مجموعة قصصية بعنوان (قلوب بلا مأوى)
قسم الشؤون الفكرية يصدر مجموعة قصصية بعنوان (قلوب بلا مأوى) قسم الشؤون الفكرية يصدر مجموعة قصصية بعنوان (قلوب بلا مأوى)
قسم الشؤون الفكرية يصدر مجموعة قصصية بعنوان (قلوب بلا مأوى)

















