


 الفيزياء الكلاسيكية
الفيزياء الكلاسيكية
 الكهربائية والمغناطيسية
الكهربائية والمغناطيسية
 علم البصريات
علم البصريات
 الفيزياء الحديثة
الفيزياء الحديثة
 النظرية النسبية
النظرية النسبية
 الفيزياء النووية
الفيزياء النووية
 فيزياء الحالة الصلبة
فيزياء الحالة الصلبة
 الليزر
الليزر
 علم الفلك
علم الفلك
 المجموعة الشمسية
المجموعة الشمسية
 الطاقة البديلة
الطاقة البديلة
 الفيزياء والعلوم الأخرى
الفيزياء والعلوم الأخرى
 مواضيع عامة في الفيزياء
مواضيع عامة في الفيزياء|
Read More
Date: 24-11-2020
Date: 13-9-2020
Date: 12-9-2020
|
Gravitational Potential Energy
Let's briefly recall our ideas about work and energy. The total work was defined as  . By substituting
. By substituting 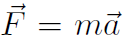 we found the work was always equal to the change in kinetic energy, i.e.
we found the work was always equal to the change in kinetic energy, i.e.
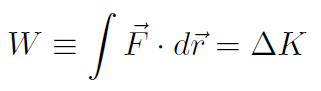
The total work consisted of two parts namely, conservative WC and non-conservative WNC. We defined potential energy U via
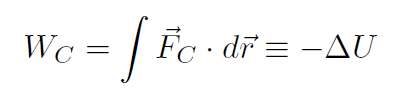
giving
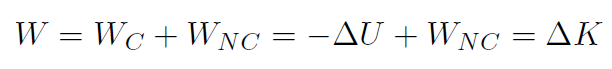
or
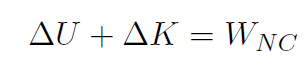
which we called the work-energy theorem. Now K is always given by 
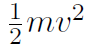 (which came from
(which came from 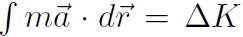 ) but U is different for different forces (because
) but U is different for different forces (because 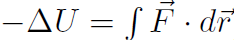 ). For a spring force
). For a spring force  we found
we found  . For gravity near the surface of Earth,
. For gravity near the surface of Earth, 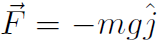 we found U = mgy. For universal gravitation
we found U = mgy. For universal gravitation 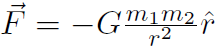 we will find that the gravitational potential energy is
we will find that the gravitational potential energy is
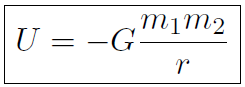
Example For gravity near the surface of Earth, prove that U = mgy.
Solution Let's do it again.
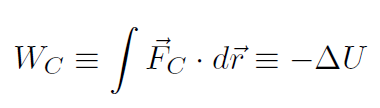
Now 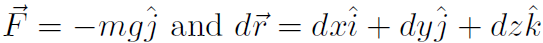 . Thus
. Thus
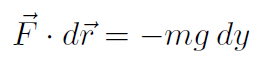
giving

giving
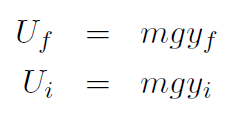
or just
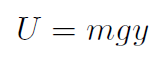
Example For universal gravitation, prove that 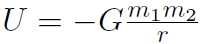 .
.
Solution
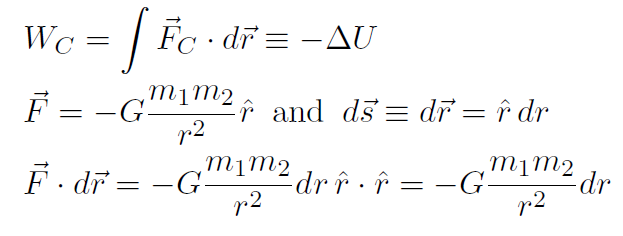
giving
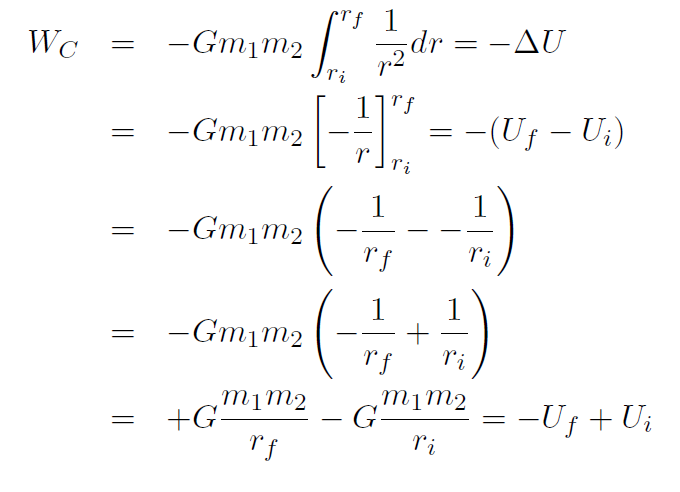
giving

or just
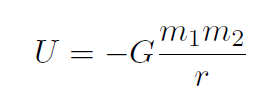
Recall that we also had an alternative way of finding U without having to work out the integral  . We had
. We had  . Ignoring the vectors we write
. Ignoring the vectors we write

meaning that we must have
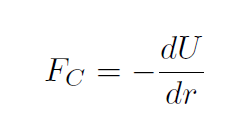
This occurs because
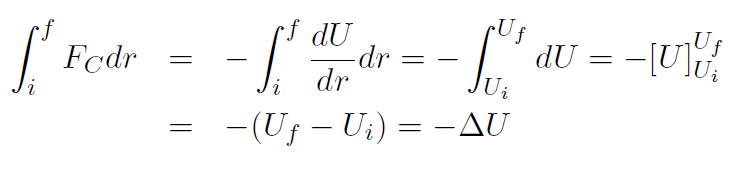
Example For universal gravitation 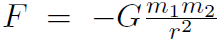 , derive U without doing an integral.
, derive U without doing an integral.
Solution For universal gravitation, the question is what U will give
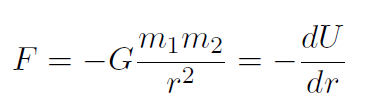
The answer is  . Let's check:
. Let's check:
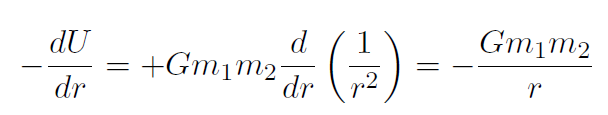
which is the F we started with!
Escape Speed
If you throw a ball up in the air it always comes back down. If you throw it faster it goes higher before returning. There is a speed, called the escape speed, such that the ball will not return at all. Let's find out what this is.
Example Calculate the speed with which a ball must be thrown, so that it never returns to the ground.
Solution The ball usually returns to the ground because of its gravitational potential energy 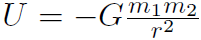 . However if we can throw the ball to an infinite distance, r = 1, then U will be zero and the ball will not return. We want to throw the ball so that it just barely escapes to infinity, that is its speed, when it gets to infinity, has dropped off to zero. Using conservation of energy we have
. However if we can throw the ball to an infinite distance, r = 1, then U will be zero and the ball will not return. We want to throw the ball so that it just barely escapes to infinity, that is its speed, when it gets to infinity, has dropped off to zero. Using conservation of energy we have
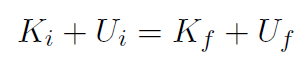
or

where M is the mass of Earth, m is the mass of the ball and R is the radius of Earth, because we throw the ball from the surface of Earth. vi is the escape speed that we are looking for. Thus
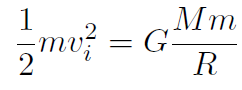
and m cancels out giving
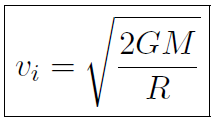
for the escape speed. Now the mass and radius of Earth are M = 6× 1024 kg and R = 6370 km, giving
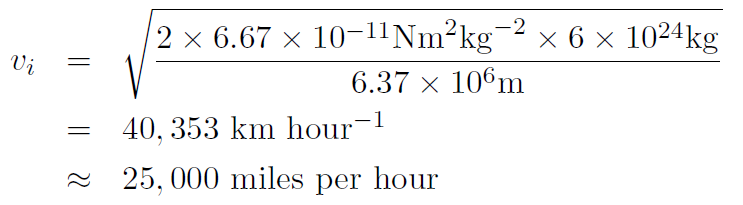
Now you can see that if M is very large or R is very small then the escape speed gets very big. The speed of light is c = 3 × 108 m/sec. You can imagine an object so massive or so small that the escape speed is bigger than the speed of light. Then light itself cannot escape. Such an object is called a Black Hole.
Example To what size would we need to squeeze Earth to turn it into a Black Hole ?
Solution Let's set the escape speed equal to the speed of light c = 3× 108 m/sec. Thus
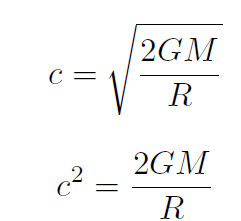
giving
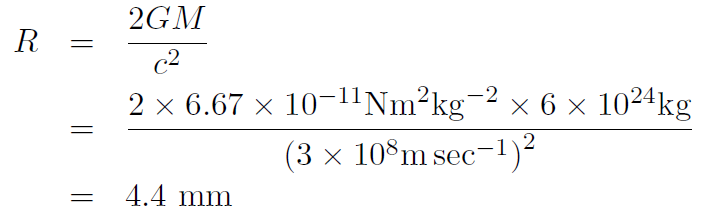
(where M = mass of Earth = 6 × 1024 kg). Thus if we could squeeze the Earth to only 4 mm it would be a black hole!
Example The size of the universe is about 10 billion light years and its total mass is about 1053 kg. Calculate the escape speed for the universe.
Solution A light year is the distance that light travels in one year. Thus
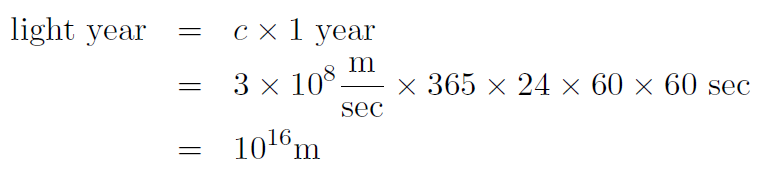
Thus
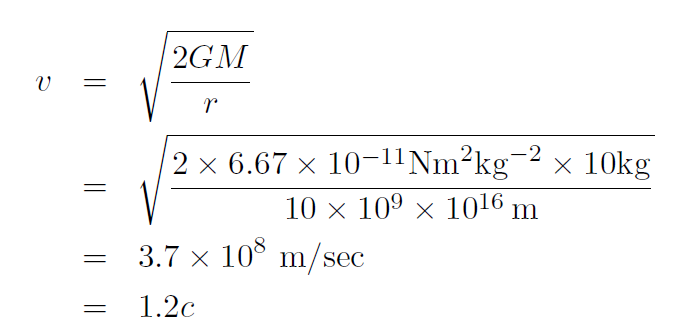
which is 1.2 times the speed of light. Thus is our universe really a black hole? Do we actually live inside a black hole?



|
|
|
|
لصحة القلب والأمعاء.. 8 أطعمة لا غنى عنها
|
|
|
|
|
|
|
حل سحري لخلايا البيروفسكايت الشمسية.. يرفع كفاءتها إلى 26%
|
|
|
|
|
|
|
جامعة الكفيل تحتفي بذكرى ولادة الإمام محمد الجواد (عليه السلام)
|
|
|